Giải bài 4.10 tr 104 SBT Toán 10
Tìm giá trị lớn nhất của hàm số
\(y = 4{x^3} - {x^4}\) với \(0 \le x \le 4\)
Hướng dẫn giải chi tiết
\(\begin{array}{l}
y = 4{x^3} - {x^4} = {x^3}\left( {4 - x} \right)\\
\Rightarrow 3y = x.x.x\left( {12 - 3x} \right) \le {\left( {\frac{{x + x}}{2}} \right)^2}.{\left( {\frac{{x + 12 - 3x}}{2}} \right)^2}\\
\Rightarrow 48 \le {\left[ {2x\left( {12 - 2x} \right)} \right]^2} \le {\left( {\frac{{2x + 12 - 2x}}{2}} \right)^4} = {6^4}\\
\Rightarrow y \le \frac{{{6^4}}}{{48}} = 27,\forall x \in \left[ {0;4} \right]\\
y = 27 \Leftrightarrow \left\{ \begin{array}{l}
x = x\\
x = 12 - 3x\\
2x = 12 - x\\
x \in \left[ {0;4} \right]
\end{array} \right. \Leftrightarrow x = 3
\end{array}\)
Vậy giá trị lớn nhất của hàm số đã cho bằng 27 đạt được khi x = 3.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 4.8 trang 104 SBT Toán 10
Bài tập 4.9 trang 104 SBT Toán 10
Bài tập 4.11 trang 104 SBT Toán 10
Bài tập 4.12 trang 104 SBT Toán 10
Bài tập 4.13 trang 104 SBT Toán 10
Bài tập 4.14 trang 105 SBT Toán 10
Bài tập 4.15 trang 105 SBT Toán 10
Bài tập 4.17 trang 105 SBT Toán 10
Bài tập 4.16 trang 105 SBT Toán 10
Bài tập 4.18 trang 105 SBT Toán 10
Bài tập 2 trang 109 SGK Toán 10 NC
Bài tập 3 trang 109 SGK Toán 10 NC
Bài tập 4 trang 109 SGK Toán 10 NC
Bài tập 5 trang 110 SGK Toán 10 NC
Bài tập 6 trang 110 SGK Toán 10 NC
Bài tập 7 trang 110 SGK Toán 10 NC
Bài tập 8 trang 110 SGK Toán 10 NC
Bài tập 9 trang 110 SGK Toán 10 NC
Bài tập 10 trang 110 SGK Toán 10 NC
Bài tập 11 trang 110 SGK Toán 10 NC
Bài tập 12 trang 110 SGK Toán 10 NC
Bài tập 13 trang 110 SGK Toán 10 NC
Bài tập 14 trang 112 SGK Toán 10 NC
Bài tập 15 trang 112 SGK Toán 10 NC
Bài tập 16 trang 112 SGK Toán 10 NC
Bài tập 17 trang 112 SGK Toán 10 NC
Bài tập 18 trang 112 SGK Toán 10 NC
-


Chứng minh 1/(a+b+1)+1/(b+c+1)+1/(a+c+1) < = 1 với a, b, c > 0 và abc=1
bởi Phương Phan Thị
 05/01/2020
Chứng minh bắt đẳng thức giúp mk vs ạ mk k bt lm câu c bài 6
05/01/2020
Chứng minh bắt đẳng thức giúp mk vs ạ mk k bt lm câu c bài 6 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh a < b và ab > 0 thì 1/a < 1/b
bởi Trần Vủ Linh
 04/01/2020
Ôn tập và bo sung tính chất của bat dang thứcTheo dõi (0) 4 Trả lời
04/01/2020
Ôn tập và bo sung tính chất của bat dang thứcTheo dõi (0) 4 Trả lời -


Tìm giá trị nhỏ nhất của hàm số f(x)=(x^2+5)/căn(x^2+4)
bởi Hạ Băng
 02/01/2020
Giải hộ em từ câu 12-15 với ạ
02/01/2020
Giải hộ em từ câu 12-15 với ạ Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -
ADMICRO


Tìm giâ trị nhỏ nhất của F(x)=x^2+5 /căn x^2+4
bởi Hạ Băng
 02/01/2020
F(x)=x2 5 /căn x2 4Theo dõi (0) 2 Trả lời
02/01/2020
F(x)=x2 5 /căn x2 4Theo dõi (0) 2 Trả lời -


Chứng minh bất đẳng thức a^5/b^2+b^5/c^2+c^5/a^2 > = a^3+b^3+c^3 với mọi a, b, c > 0
bởi Nguyễn Xuân Linh
 01/01/2020
Bài 19
01/01/2020
Bài 19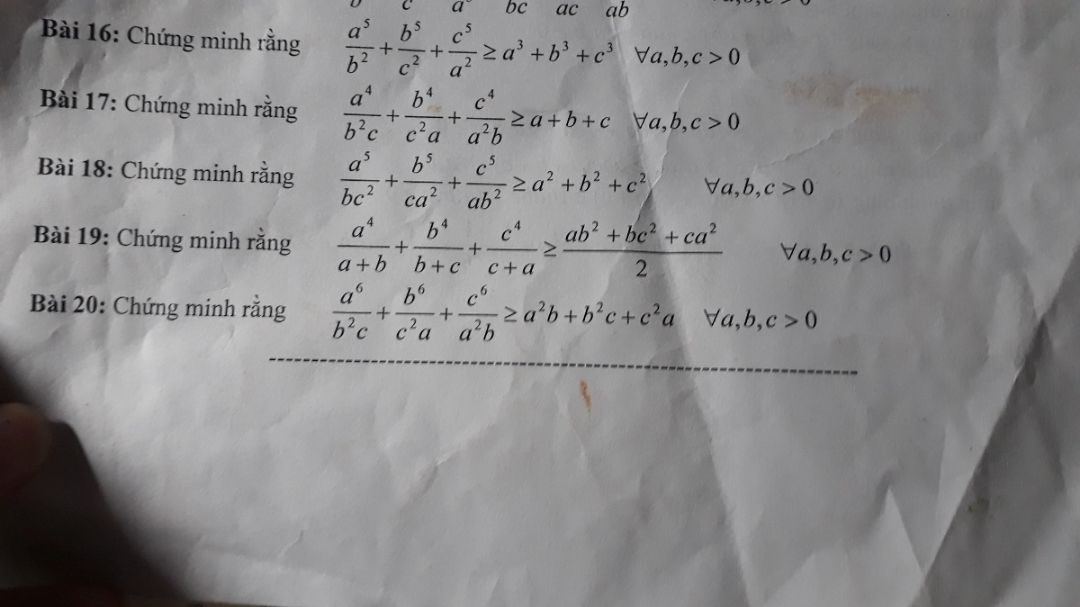 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 1/(2 a^2b) 1/(2 b^2c) 1/(2 c^ 2a) > = 1 biết a b c=3.Theo dõi (0) 0 Trả lời
1/(2 a^2b) 1/(2 b^2c) 1/(2 c^ 2a) > = 1 biết a b c=3.Theo dõi (0) 0 Trả lời -


Chứng minh a^4+b^4+c^2+1 > = 2(a^2b-a+c+1)
bởi Sông Hương
 30/12/2019
30/12/2019
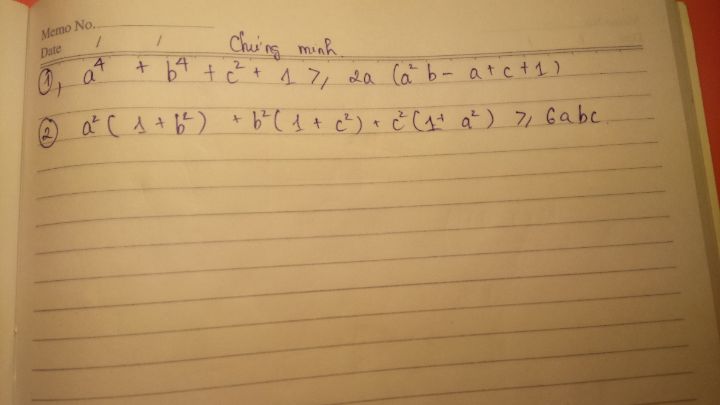 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm GTLN của hàm số y=(x-3)(*7-x) với 3 < = x < = 7
bởi Thư Nguyên
 29/12/2019
29/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời





