Giải bài 4.11 tr 104 SBT Toán 10
Tìm giá trị lớn nhất, nhỏ nhất của hàm số sau trên tập xác định của nó:
\(y = \sqrt {x - 1} + \sqrt {5 - x} \)
Hướng dẫn giải chi tiết
Hàm số có nghĩa khi \(1 \le x \le 5\)
Ta có :
\(\begin{array}{l}
{y^2} = {\left( {\sqrt {x - 1} + \sqrt {5 - x} } \right)^2} = 4 + 2\sqrt {\left( {x - 1} \right)\left( {5 - x} \right)} \\
\Rightarrow \left\{ \begin{array}{l}
{y^2} \ge 4,\forall x \in \left[ {1;5} \right]\\
{y^2} \le 4 + \left( {x - 1} \right) + \left( {5 - x} \right) = 8
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
y \ge 2\\
y \le 2\sqrt 2
\end{array} \right.,\forall x \in \left[ {1;5} \right]
\end{array}\)
Hơn nữa \(y = 2 \Leftrightarrow \left( {x - 1} \right)\left( {5 - x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x = 5
\end{array} \right.\)
\(y = 2\sqrt 2 \Leftrightarrow x - 1 = 5 - x \Leftrightarrow x = 3\)
Vậy giá trị lớn nhất của hàm số đã cho bằng \(2\sqrt 2\) khi x = 3, giá trị nhỏ nhất của hàm số đã cho bằng 2 khi x = 1 hoặc x = 5.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 4.9 trang 104 SBT Toán 10
Bài tập 4.10 trang 104 SBT Toán 10
Bài tập 4.12 trang 104 SBT Toán 10
Bài tập 4.13 trang 104 SBT Toán 10
Bài tập 4.14 trang 105 SBT Toán 10
Bài tập 4.15 trang 105 SBT Toán 10
Bài tập 4.17 trang 105 SBT Toán 10
Bài tập 4.16 trang 105 SBT Toán 10
Bài tập 4.18 trang 105 SBT Toán 10
Bài tập 2 trang 109 SGK Toán 10 NC
Bài tập 3 trang 109 SGK Toán 10 NC
Bài tập 4 trang 109 SGK Toán 10 NC
Bài tập 5 trang 110 SGK Toán 10 NC
Bài tập 6 trang 110 SGK Toán 10 NC
Bài tập 7 trang 110 SGK Toán 10 NC
Bài tập 8 trang 110 SGK Toán 10 NC
Bài tập 9 trang 110 SGK Toán 10 NC
Bài tập 10 trang 110 SGK Toán 10 NC
Bài tập 11 trang 110 SGK Toán 10 NC
Bài tập 12 trang 110 SGK Toán 10 NC
Bài tập 13 trang 110 SGK Toán 10 NC
Bài tập 14 trang 112 SGK Toán 10 NC
Bài tập 15 trang 112 SGK Toán 10 NC
Bài tập 16 trang 112 SGK Toán 10 NC
Bài tập 17 trang 112 SGK Toán 10 NC
Bài tập 18 trang 112 SGK Toán 10 NC
-


Chứng minh với 3 số a, b, c không âm ta luôn có (a+b+c)/3 > = căn bậc 3 của abc
bởi Phạm Thắm
 23/12/2019
23/12/2019
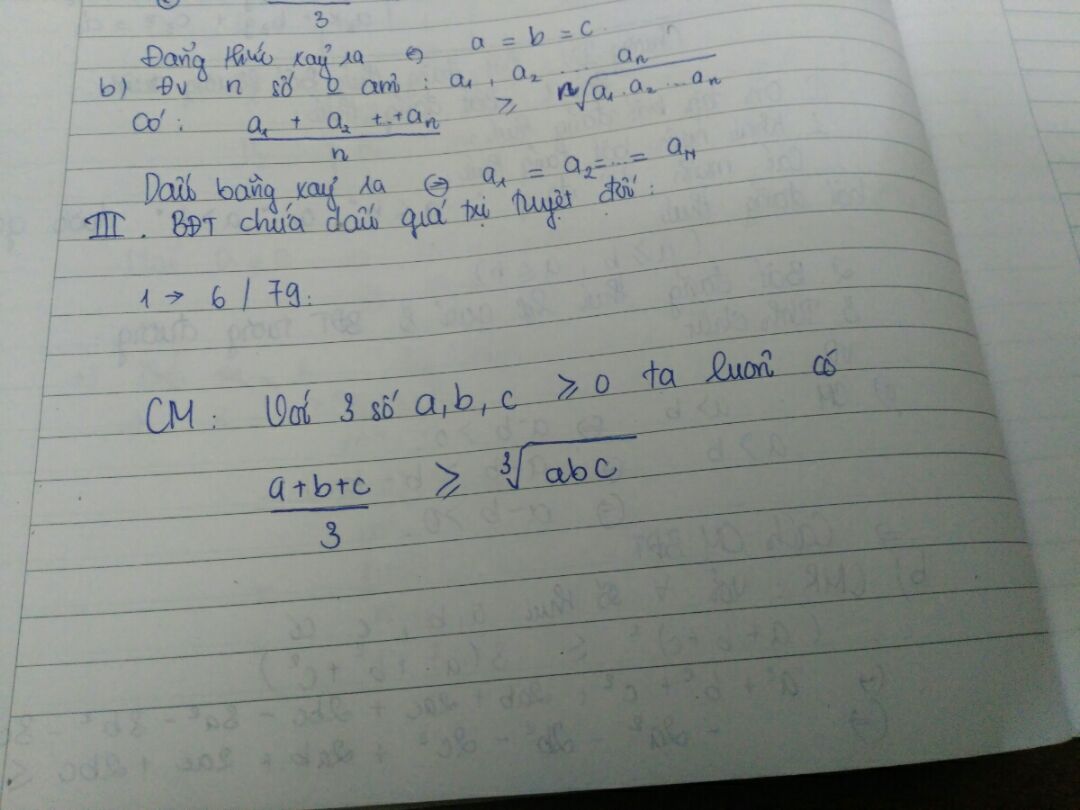 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm GTNN của hàm số y=(x^2+4)/x
bởi Mai Ngoc
 19/12/2019
Y=x^2 4/x
19/12/2019
Y=x^2 4/x Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (2) 2 Trả lời
Theo dõi (2) 2 Trả lời -


Trong các tính chất sau, tính chất nào sai?
bởi Trần Huy
 17/12/2019
Câu 11
17/12/2019
Câu 11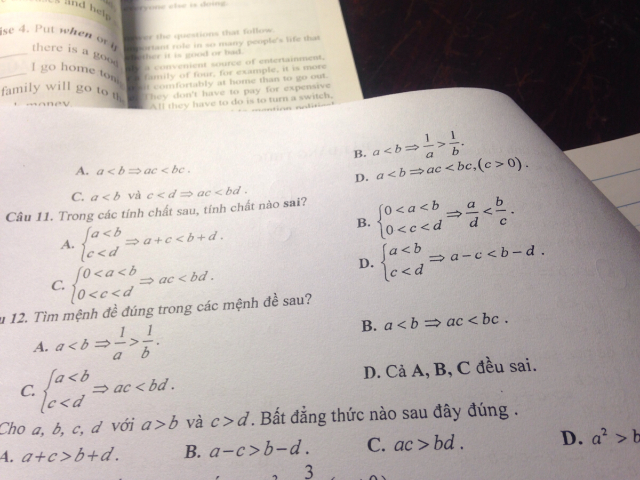 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -
ADMICRO


Tìm GTNN của hàm số f(x)=(x^2+2x+2)/(x+1)
bởi Thục Quyên
 16/12/2019
Câu 31
16/12/2019
Câu 31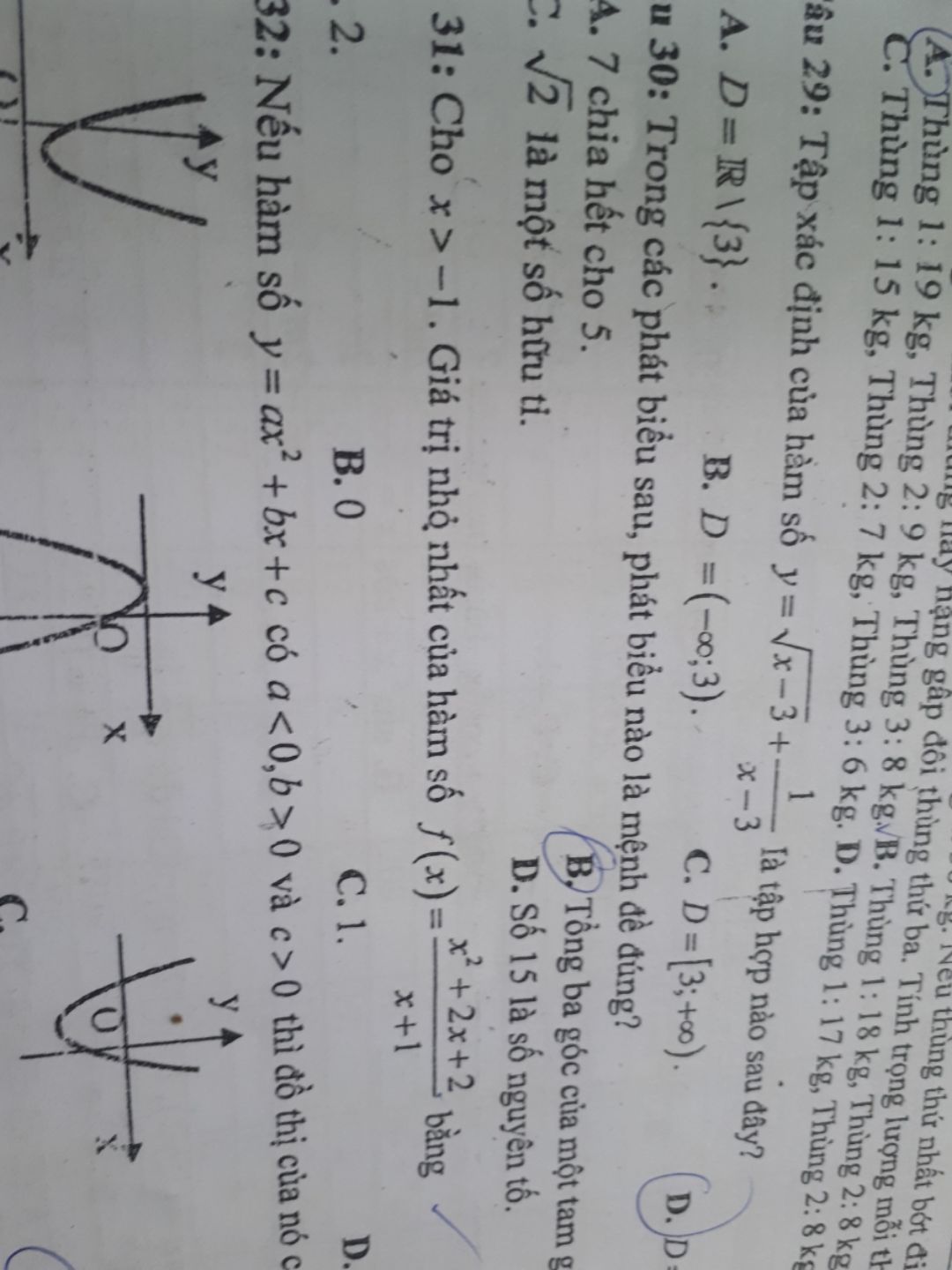 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm giá trị nhỏ nhất của hàm số y = sqrt(7-2x) + sqrt(3x+4)
Theo dõi (2) 1 Trả lời -

 Đề trường chuyên HN
Đề trường chuyên HN Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Trong hình ạ
Trong hình ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Câu 39 ạ, mn giải dùm em vs
Câu 39 ạ, mn giải dùm em vs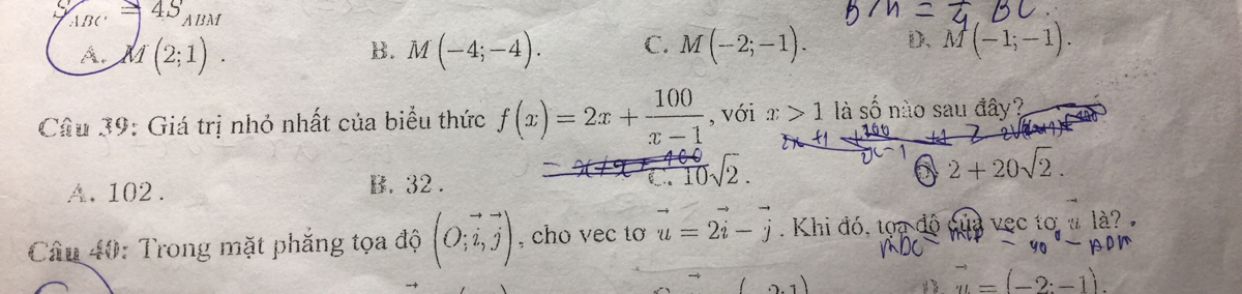 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời






