Giải bài 4.5 tr 104 SBT Toán 10
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
\({a^2}b + \frac{1}{b} \ge 2a\)
Hướng dẫn giải chi tiết
\({a^2}b + \frac{1}{b} \ge 2\sqrt {{a^2}b.\frac{1}{b}} = 2a\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 4.3 trang 104 SBT Toán 10
Bài tập 4.4 trang 104 SBT Toán 10
Bài tập 4.6 trang 104 SBT Toán 10
Bài tập 4.7 trang 104 SBT Toán 10
Bài tập 4.8 trang 104 SBT Toán 10
Bài tập 4.9 trang 104 SBT Toán 10
Bài tập 4.10 trang 104 SBT Toán 10
Bài tập 4.11 trang 104 SBT Toán 10
Bài tập 4.12 trang 104 SBT Toán 10
Bài tập 4.13 trang 104 SBT Toán 10
Bài tập 4.14 trang 105 SBT Toán 10
Bài tập 4.15 trang 105 SBT Toán 10
Bài tập 4.17 trang 105 SBT Toán 10
Bài tập 4.16 trang 105 SBT Toán 10
Bài tập 4.18 trang 105 SBT Toán 10
Bài tập 2 trang 109 SGK Toán 10 NC
Bài tập 3 trang 109 SGK Toán 10 NC
Bài tập 4 trang 109 SGK Toán 10 NC
Bài tập 5 trang 110 SGK Toán 10 NC
Bài tập 6 trang 110 SGK Toán 10 NC
Bài tập 7 trang 110 SGK Toán 10 NC
Bài tập 8 trang 110 SGK Toán 10 NC
Bài tập 9 trang 110 SGK Toán 10 NC
Bài tập 10 trang 110 SGK Toán 10 NC
Bài tập 11 trang 110 SGK Toán 10 NC
Bài tập 12 trang 110 SGK Toán 10 NC
Bài tập 13 trang 110 SGK Toán 10 NC
Bài tập 14 trang 112 SGK Toán 10 NC
Bài tập 15 trang 112 SGK Toán 10 NC
Bài tập 16 trang 112 SGK Toán 10 NC
Bài tập 17 trang 112 SGK Toán 10 NC
Bài tập 18 trang 112 SGK Toán 10 NC
-
Tìm giá trị nhỉ nhất của biểu thức A?
bởi Hương Hương
05/06/2020
Lời giải
câu 16
Theo dõi (0) 0 Trả lời -
Tìm m để BPT đúng với mọi x>2?
bởi Việt Hùng
01/06/2020
Tìm m để BPT:
(m-3)x2 -10(m-2)x+23m-24>0 với mọi x>2
Theo dõi (0) 2 Trả lời -
Tìm số điền vào chỗ trống để được mệnh đề đúng
bởi Bảo Uyên
26/05/2020
Giải tự luận hộ mình câu 1 và câu 3 ạ
Theo dõi (0) 1 Trả lời -
Tìm GTLN của A?
bởi Ngọc Diễm
12/05/2020
.
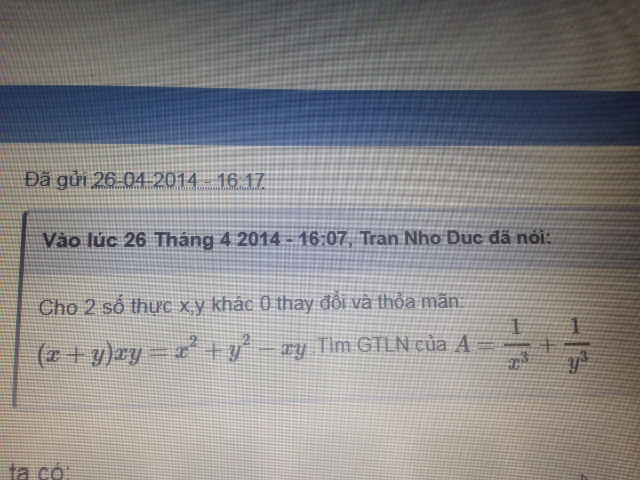Theo dõi (0) 1 Trả lời -
ADMICRO
Chứng minh a^4/( a+b) + b^4 /(b+c) +c^4/(c+a)>= ( a*b^2 + b*c^2+c*a^2)/2
bởi Huỳnh Tấn Nhã
04/05/2020
a^4/( a+b) + b^4 /(b+c) +c^4/(c+a)>= ( a*b^2 + b*c^2+c*a^2)/2 a,b,c > 0
Theo dõi (0) 0 Trả lời -
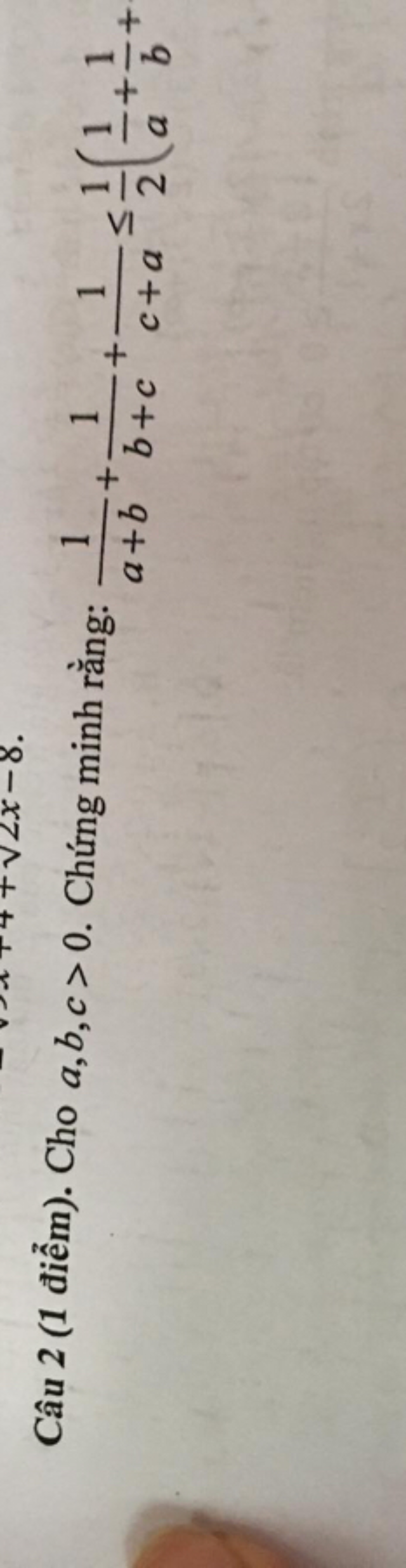Theo dõi (0) 1 Trả lời -
cho a,b,c dương chứng minh a^2/(b 2c) b^2/(c 2a) c^2/(a 2b)>=(a b c)/3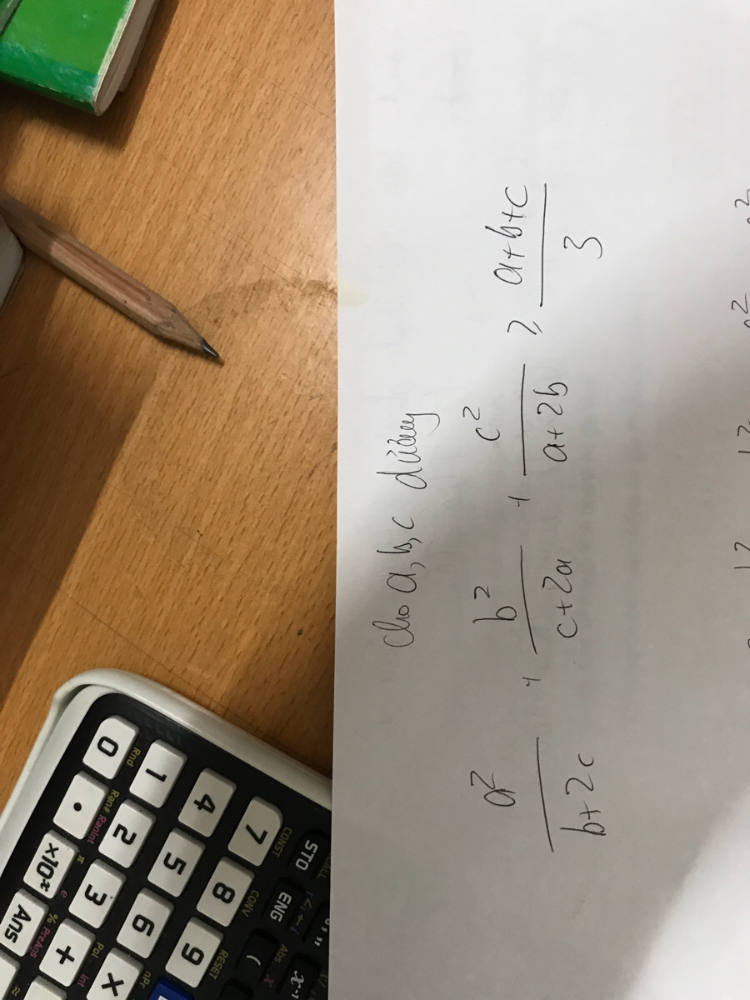
Theo dõi (0) 2 Trả lời -
Tìm GTNN của biểu thức P?
bởi Long
15/04/2020
P=2x 8/x^2
Câu 2
Theo dõi (0) 0 Trả lời -
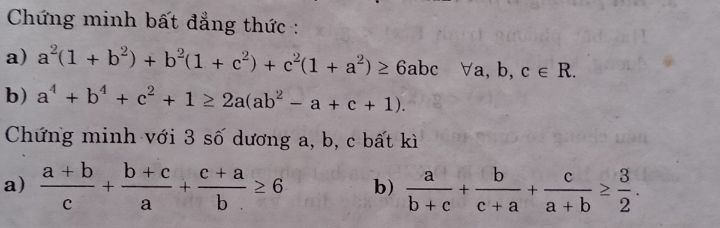Theo dõi (0) 0 Trả lời
