Bài tập 52 trang 177 SGK Toán 12 NC
Tính diện tích của các hình phẳng giới hạn bởi:
a) Parabol y = x2 − 2x + 2, tiếp tuyến của nó tại điểm M(3; 5) và trục tung
b) Parabol y = −x2 + 4x − 3y và các tiếp tuyến của nó tại các điểm A(0;−3) và B(3;0)
Hướng dẫn giải chi tiết
a)
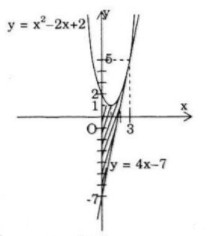
Ta có y′ = 2x − 2 ⇒ y′(3) = 4
Phương trình tiếp tuyến với parabol tại M(3;5) là:
y − 5 = 4(x − 3) ⇔ y = 4x − 7
Gọi S là diện tích cần tìm, ta có:
\(\begin{array}{*{20}{l}}
{S = \int_0^3 {({x^2} - 2x + 2 - 4x + 7)dx} }\\
\begin{array}{l}
= \int_0^3 {({x^2} - 6x + 9)dx} \\
= \int_0^3 {{{(x - 3)}^2}dx}
\end{array}\\
{ = \left. {\frac{1}{3}{{\left( {x - 3} \right)}^3}} \right|_0^3 = 9}
\end{array}\)
b)
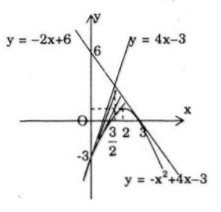
Ta có y′ = −2x + 4 ⇒ y′(0) = 4; y′(3) = −2
Phương trình tiếp tuyến tại A(0; 3) là: y + 3 = 4(x − 0) ⇔ y = 4x − 3
Phương trình tiếp tuyến tại B(3; 0) là: y = −2(x − 3) ⇔ y = −2x + 6
Giao điểm của hai tiếp tuyến là C(3/2;3).
Kí hiệu A1 và A2 là tam giác cong ACD Và BCD. Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
S({A_1}) = \int_0^{\frac{3}{2}} {(4x - 3 + {x^2} - 4x + 3)dx} \\
= \int_0^{\frac{3}{2}} {{x^2}dx} = \left. {\frac{{{x^3}}}{3}} \right|_0^{\frac{3}{2}} = \frac{9}{8}
\end{array}\\
\begin{array}{l}
S({A_2}) = \int_{\frac{3}{2}}^3 {( - 2x + 6 + {x^2} - 4x + 3)dx} \\
= \int_{\frac{3}{2}}^3 {{{(x - 3)}^2}dx} = \left. {\frac{1}{3}{{(x - 3)}^3}} \right|_{\frac{3}{2}}^3 = \frac{9}{8}
\end{array}
\end{array}\)
Vậy \(S = S({A_1}) + S({A_2}) = \frac{9}{8} + \frac{9}{8} = \frac{9}{4}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 50 trang 176 SGK Toán 12 NC
Bài tập 51 trang 176 SGK Toán 12 NC
Bài tập 53 trang 177 SGK Toán 12 NC
Bài tập 54 trang 177 SGK Toán 12 NC
Bài tập 55 trang 177 SGK Toán 12 NC
Bài tập 56 trang 177 SGK Toán 12 NC
Bài tập 57 trang 177 SGK Toán 12 NC
Bài tập 58 trang 177 SGK Toán 12 NC
Bài tập 59 trang 177 SGK Toán 12 NC
Bài tập 60 trang 178 SGK Toán 12 NC
Bài tập 61 trang 178 SGK Toán 12 NC
Bài tập 62 trang 178 SGK Toán 12 NC
Bài tập 63 trang 178 SGK Toán 12 NC
Bài tập 64 trang 178 SGK Toán 12 NC
Bài tập 65 trang 178 SGK Toán 12 NC
Bài tập 66 trang 179 SGK Toán 12 NC
Bài tập 67 trang 179 SGK Toán 12 NC
Bài tập 3.43 trang 180 SBT Toán 12
Bài tập 3.44 trang 180 SBT Toán 12
Bài tập 3.45 trang 181 SBT Toán 12
Bài tập 3.46 trang 181 SBT Toán 12
Bài tập 3.47 trang 181 SBT Toán 12
Bài tập 3.48 trang 181 SBT Toán 12
Bài tập 3.49 trang 182 SBT Toán 12
Bài tập 3.50 trang 182 SBT Toán 12
Bài tập 3.51 trang 182 SBT Toán 12
Bài tập 3.52 trang 182 SBT Toán 12
Bài tập 3.53 trang 183 SBT Toán 12
Bài tập 3.54 trang 183 SBT Toán 12
Bài tập 3.55 trang 183 SBT Toán 12
Bài tập 3.56 trang 183 SBT Toán 12
Bài tập 3.67 trang 183 SBT Toán 12
Bài tập 3.58 trang 184 SBT Toán 12
-


A. \(I = \dfrac{1}{2}\).
B. \(I = \dfrac{{3{e^2} + 1}}{4}\).
C. \(I = \dfrac{{{e^2} + 1}}{4}\).
D. \(I = \dfrac{{{e^2} - 1}}{4}\).
Theo dõi (0) 1 Trả lời -


Hãy tìm hai số thực A, B sao cho \(f(x) = A\sin \pi x + B\), biết f’(1) = 2 và \(\int\limits_0^2 {f(x)\,dx = 4} \).
bởi Nhật Nam
 05/05/2021
05/05/2021
A. \(\left\{ \begin{array}{l}A = - 2\\B = - \dfrac{2}{\pi }\end{array} \right.\).
B. \(\left\{ \begin{array}{l}A = 2\\B = - \dfrac{2}{\pi }\end{array} \right.\).
C. \(\left\{ \begin{array}{l}A = - 2\\B = \dfrac{2}{\pi }\end{array} \right.\).
D. \(\left\{ \begin{array}{l}B = 2\\A = - \dfrac{2}{\pi }\end{array} \right.\)
Theo dõi (0) 1 Trả lời -


Cho \(\int\limits_0^{\dfrac{x}{3}} {\dfrac{{\sin 2x}}{{1 + \cos x}}\,dx} \). Thực hiện phép đổi biến t = cosx, ta có thể đưa I về dạng nào sau đây?
bởi Thiên Mai
 06/05/2021
06/05/2021
A. \(I = \int\limits_{\dfrac{1}{2}}^1 {\dfrac{{2t}}{{1 + 1}}\,dt} \).
B. \(I = \int\limits_{\dfrac{0}{2}}^{\dfrac{x}{4}} {\dfrac{{2t}}{{1 + 1}}\,dt} \).
C. \(I = - \int\limits_{\dfrac{1}{2}}^1 {\dfrac{{2t}}{{1 + 1}}\,dt} \).
D. \(I = - \int\limits_{\dfrac{0}{2}}^{\dfrac{x}{4}} {\dfrac{{2t}}{{1 + 1}}\,dt} \).
Theo dõi (0) 1 Trả lời -


Cho hàm số f(x) liên tục trên đoạn [a ; b]. Chọn phương án sai trong các phương án sau:
bởi Việt Long
 05/05/2021
05/05/2021
A. \(\int\limits_a^b {f(x)\,dx = \int\limits_b^a {f(x)\,dx} } \).
B. \(\int\limits_a^b {k.dx = k\left( {b - a} \right),\,\forall k \in R} \).
C. \(\int\limits_a^b {f(x)\,dx = - \int\limits_b^a {f(x)\,dx} } \)
D. \(\int\limits_a^b {f(x)\,dx = \int\limits_a^c {f(x)\,dx + \int\limits_c^b {f(x)\,dx\,,\,\,\,c \in [a;b]} } } \)
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho tích phân \(\int\limits_{ - 2}^1 {f(x)\,dx = 1,\,\,\int\limits_{ - 2}^1 {g(x)\,dx = - 2} } \). Tính \(\int\limits_{ - 2}^1 {\left( {1 - f(x) + 3g(x)} \right)} \,dx\) bằng giá trị nào dưới đây?
bởi Cam Ngan
 06/05/2021
06/05/2021
A. 24
B. – 7
C. – 4
D. 8
Theo dõi (0) 1 Trả lời -


Hàm số y = f(x) liên tục trên đoạn [a ;b]. Cho biết diện tích hình phẳng giới hạn bởi đường cong y = f(x), trục hoành, các đường thẳng x = a, x = b là:
bởi Mai Thuy
 05/05/2021
05/05/2021
A. \(\int\limits_a^b {\left| {f(a)} \right|\,dx} \).
B. \( - \int\limits_a^b {f(x)\,dx} \).
C. \(\int\limits_b^a {f(x)\,dx} \).
D. \(\int\limits_a^b {f(x)\,dx} \).
Theo dõi (0) 1 Trả lời -


Tích phân \(\int\limits_0^4 {\left( {3x - {e^{\dfrac{x}{2}}}} \right)dx = a + b{e^2}} \) khi đó a – 10b bằng bao nhiêu?
bởi Thúy Vân
 06/05/2021
06/05/2021
A. 6
B 46
C. 26
D. 12
Theo dõi (0) 1 Trả lời



