Bài tập 3.47 trang 181 SBT Toán 12
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi
a) \(y = {x^{\frac{2}{3}}},x = 0\) và tiếp tuyến với đường \(y = {x^{\frac{2}{3}}}\) tại điểm có hoành độ x = 1, quanh trục Oy;
b) \(y = \frac{1}{x} - 1,y = 0,y = 2x\), quanh trục Ox.
c) \(y = \left| {2x - {x^2}} \right|,y = 0\) và x = 3, quanh :
* Trục Ox
* Trục Oy
Hướng dẫn giải chi tiết
a) Ta có: \(y' = \frac{2}{3}{x^{ - \frac{1}{3}}}\)
Với x = 1 thì y = 1 và \(y'\left( 1 \right) = \frac{2}{3}\).
Tiếp tuyến \(y = \frac{2}{3}\left( {x - 1} \right) + 1 = \frac{2}{3}x + \frac{1}{3}\)
Có \(y = {x^{\frac{2}{3}}} \Rightarrow x = {y^{\frac{3}{2}}}\) và
\(y = \frac{2}{3}x + \frac{1}{3} \Rightarrow x = \frac{3}{2}y - \frac{1}{2}\)
Khi đó \({y^{\frac{3}{2}}} = \frac{3}{2}y - \frac{1}{2} \Rightarrow y = 1\).
Ta có: \(\frac{3}{2}y - \frac{1}{2} = 0 \Leftrightarrow y = \frac{1}{3}\)
\(\begin{array}{l}
V = \pi \int \limits_0^1 {\left( {{y^{\frac{3}{2}}}} \right)^2}dy - \pi \int \limits_{\frac{1}{3}}^1 {\left( {\frac{3}{2}y - \frac{1}{2}} \right)^2}dy\\
= \pi \int \limits_0^1 {y^3}dy - \pi \int \limits_{\frac{1}{3}}^1 {\left( {\frac{3}{2}y - \frac{1}{2}} \right)^2}dy\\
= \pi .\left. {\frac{{{y^4}}}{4}} \right|_0^1 - \pi \int\limits_{\frac{1}{3}}^1 {\left( {\frac{9}{4}{y^2} - \frac{3}{2}y + \frac{1}{4}} \right)dy} \\
= \frac{\pi }{4} - \pi .\left. {\left( {\frac{3}{4}{y^3} - \frac{3}{4}{y^3} + \frac{1}{4}y} \right)} \right|_{\frac{1}{3}}^1\\
= \frac{\pi }{4} - \frac{{2\pi }}{9} = \frac{\pi }{{36}}
\end{array}\)
b) Ta có:
\(\begin{array}{l}
\frac{1}{x} - 1 = 2x \Rightarrow x = \frac{1}{2}\\
\frac{1}{x} - 1 = 0 \Leftrightarrow x = 1\\
2x = 0 \Leftrightarrow x = 0
\end{array}\)
Do đó
\(\begin{array}{l}
V = \pi \int \limits_0^{\frac{1}{2}} {\left( {2x} \right)^2}dx + \pi \int \limits_{\frac{1}{2}}^1 {\left( {\frac{1}{x} - 1} \right)^2}dx\\
= \pi .\int \limits_0^{\frac{1}{2}} 4{x^2}dx + \pi .\int \limits_{\frac{1}{2}}^1 \left( {\frac{1}{{{x^2}}} - \frac{2}{x} + 1} \right)dx\\
= \pi .\left. {\frac{{4{x^3}}}{3}} \right|_0^{\frac{1}{2}} + \pi \left. {\left( { - \frac{1}{x} - 2\ln x + x} \right)} \right|_{\frac{1}{2}}^1\\
= \frac{\pi }{6} + \pi \left( {0 + 2 + 2\ln \frac{1}{2} - \frac{1}{2}} \right)\\
= \frac{\pi }{6} + \frac{{3\pi }}{2} - 2\pi \ln 2\\
= \frac{{5\pi }}{3} - 2\pi \ln 2
\end{array}\)
c) +) Quay quanh Ox.
Ta có: \(\left| {2x - {x^2}} \right| = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 2.
\end{array} \right.\)
Khi đó
\(\begin{array}{l}
V = \pi \int \limits_0^3 {\left( {2x - {x^2}} \right)^2}dx\\
= \pi \int \limits_0^3 \left( {4{x^2} - 4{x^3} + {x^4}} \right)dx\\
= \pi \left. {\left( {\frac{{4{x^3}}}{3} - {x^4} + \frac{{{x^5}}}{5}} \right)} \right|_0^3\\
= \pi \left( {\frac{{4.27}}{3} - {3^4} + \frac{{{3^5}}}{5}} \right) = \frac{{18\pi }}{5}
\end{array}\)
+) Quay quanh Oy.
Ta có:
\(\begin{array}{l}
y = \left| {2x - {x^2}} \right| \Rightarrow \left[ \begin{array}{l}
y = 2x - {x^2}\\
y = - 2x + {x^2}
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
{x^2} - 2x + y = 0\\
{x^2} - 2x - y = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = 1 \pm \sqrt {1 - y} \\
x = 1 \pm \sqrt {1 + y}
\end{array} \right.
\end{array}\)
Ta có:
\(\begin{array}{l}
{V_y} = \pi \int \limits_0^1 \left[ {{{\left( {1 + \sqrt {1 - y} } \right)}^2} - {{\left( {1 - \sqrt {1 - y} } \right)}^2}} \right]dy\\
+ \pi \int \limits_0^3 \left[ {{3^2} - {{\left( {1 + \sqrt {1 + y} } \right)}^2}} \right]dy\\
= \pi \int \limits_0^1 \left( {1 + 2\sqrt {1 - y} + 1 - y - 1 + 2\sqrt {1 - y} - 1 + y} \right)dy\\
+ \pi \int\limits_0^3 {\left( {9 - 1 - 2\sqrt {1 + y} - 1 - y} \right)dy} \\
= \pi \int \limits_0^1 4\sqrt {1 - y} dy + \pi \int \limits_0^3 \left( {7 - y - 2\sqrt {1 + y} } \right)dy\\
= 4\pi \int \limits_0^1 \sqrt {1 - y} dy + \pi \left[ {\left. {\left( {7y - \frac{{{y^2}}}{2}} \right)} \right|_0^3 - 2\int\limits_0^3 {\sqrt {1 + y} dy} } \right]\\
= 4\pi I + \pi (\frac{{33}}{2} - 2J)
\end{array}\)
Tính \(I = \int \limits_0^1 \sqrt {1 - y} dy\) ta có:
Đặt \(\sqrt {1 - y} = t \Rightarrow 1 - y = {t^2}\)
\(\begin{array}{l}
\Rightarrow - dy = 2tdt \Rightarrow dy = - 2tdt\\
\Rightarrow I = \int \limits_1^0 t.\left( { - 2tdt} \right) = \int\limits_0^1 {2{t^2}dt} \\
= \left. {\frac{2}{3}{t^3}} \right|_0^1 = \frac{2}{3}
\end{array}\)
Tính \(J = \int \limits_0^3 \sqrt {1 + y} dy\) ta có:
Đặt \(t = \sqrt {1 + y} \Rightarrow {t^2} = 1 + y\)
\(\Rightarrow 2tdt = dy\)
\( \Rightarrow J = \int\limits_1^2 {t.2tdt} = \left. {\frac{{2{t^3}}}{3}} \right|_1^2 = \frac{{14}}{3}\)
Vậy \(V = 4\pi .\frac{2}{3} + \pi \left( {\frac{{33}}{2} - 2.\frac{{14}}{3}} \right) = \frac{{59\pi }}{6}\).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.45 trang 181 SBT Toán 12
Bài tập 3.46 trang 181 SBT Toán 12
Bài tập 3.48 trang 181 SBT Toán 12
Bài tập 3.49 trang 182 SBT Toán 12
Bài tập 3.50 trang 182 SBT Toán 12
Bài tập 3.51 trang 182 SBT Toán 12
Bài tập 3.52 trang 182 SBT Toán 12
Bài tập 3.53 trang 183 SBT Toán 12
Bài tập 3.54 trang 183 SBT Toán 12
Bài tập 3.55 trang 183 SBT Toán 12
Bài tập 3.56 trang 183 SBT Toán 12
Bài tập 3.67 trang 183 SBT Toán 12
Bài tập 3.58 trang 184 SBT Toán 12
-


Cho hàm số f(x) thỏa mãn f(x) + 1/2.f'(x) = 1/e^2x, biết f(0) = 1. Tìm hàm số f(x)
bởi Đỗ Thành
 20/03/2021
Giúp em
20/03/2021
Giúp em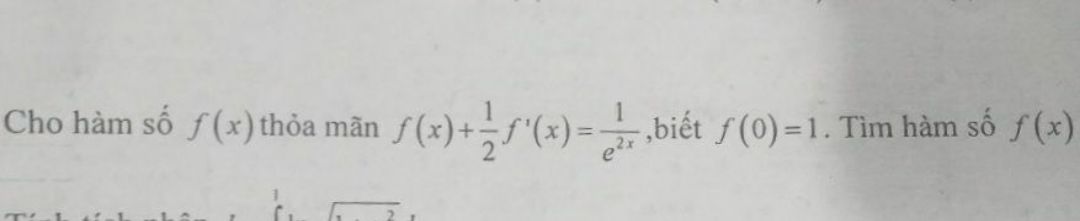 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

a)
. Tính P = a - b + c
b) Biết
. Tính
Theo dõi (0) 0 Trả lời -


Câu 39,40,41,42 help
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm F(x)?
bởi Trần Bảo
 18/06/2020
18/06/2020
Câu 6. Nguyên hàm f(x)=x 2018
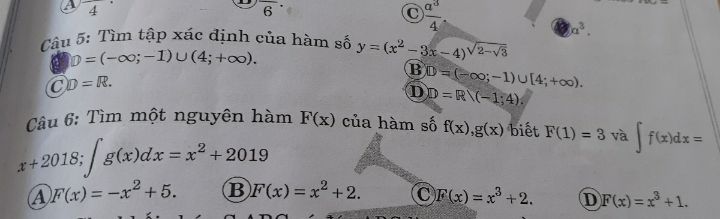 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Khẳng định nào sau đây sai, biết \(\int\limits_{ - 1}^0 {\left| {\frac{{x + 1}}{{x - 2}}} \right|} dx = a\ln \frac{b}{c} - 1\)?
bởi Trang Khuu
 03/06/2020
03/06/2020
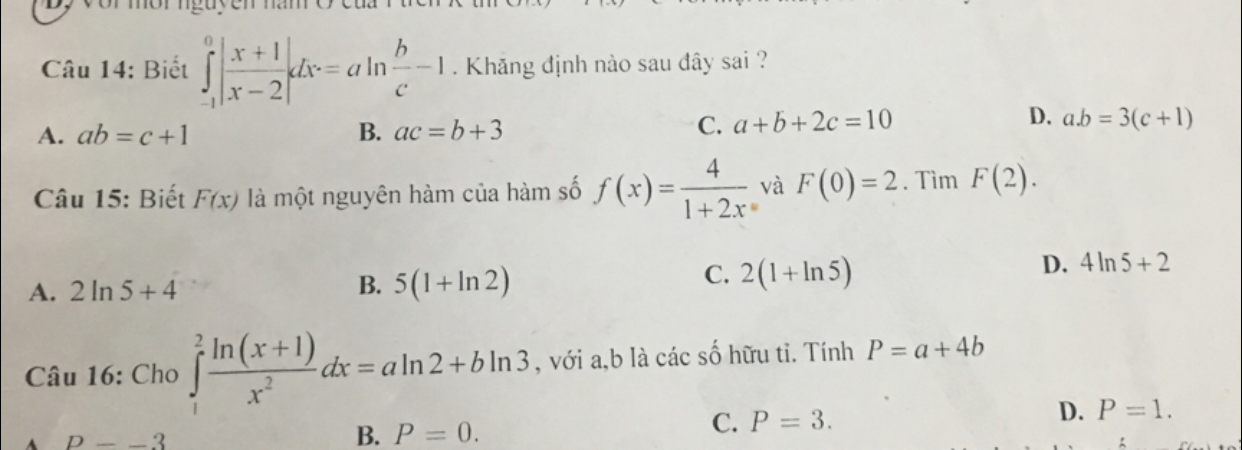 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của hàm số (f(x) = 2sin x)
bởi Mai Bảo Khánh
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời



