Bài tập 3.48 trang 181 SBT Toán 12
Hãy chỉ ra các kết quả đúng trong các kết quả sau:
a) \(\int \limits_0^1 {x^n}{(1 - x)^m}dx = \int \limits_0^1 {x^m}{(1 - x)^n}dx;m,n \in {N^ * }\)
b) \(\int \limits_{ - 1}^1 \frac{{{t^2}}}{{{e^t} + 1}}dt = \int \limits_0^1 {t^2}dt\)
c) \(\int \limits_0^1 {\sin ^3}x\cos xdx = \int \limits_0^1 {t^3}dt\)
Hướng dẫn giải chi tiết
a) Đúng vì trong tích phân \(\int \limits_0^1 {x^n}{(1 - x)^m}dx\), nếu đặt t = 1−x thì dx = −dt
\(\begin{array}{l}
\Rightarrow \int \limits_0^1 {x^n}{(1 - x)^m}dx = \int \limits_1^0 {\left( {1 - t} \right)^n}.{t^m}.\left( { - dt} \right)\\
= \int \limits_0^1 {t^m}.{\left( {1 - t} \right)^n}dt = \int \limits_0^1 {x^m}.{\left( {1 - x} \right)^n}dt
\end{array}\)
b) Ta có:
\(\int \limits_{ - 1}^1 \frac{{{t^2}dt}}{{{e^t} + 1}} = \int \limits_{ - 1}^0 \frac{{{t^2}dt}}{{{e^t} + 1}} + \int \limits_0^1 \frac{{{t^2}dt}}{{{e^t} + 1}}\) (*)
Dùng phương pháp đổi biến t = −x đối với tích phân \(\int \limits_{ - 1}^0 \frac{{{t^2}dt}}{{{e^t} + 1}}\), ta được:
\(\begin{array}{l}
\int \limits_{ - 1}^0 \frac{{{t^2}dt}}{{{e^t} + 1}} = \int \limits_0^1 \frac{{{x^2}dx}}{{{e^{ - x}} + 1}}\\
= \int \limits_0^1 \frac{{{t^2}dt}}{{{e^{ - t}} + 1}} = \int \limits_0^1 \frac{{{t^2}{e^t}}}{{1 + {e^t}}}dt
\end{array}\)
Thay vào (*) ta có:
\(\begin{array}{l}
\int \limits_{ - 1}^1 \frac{{{t^2}dt}}{{{e^t} + 1}} = \int \limits_0^1 \frac{{{t^2}{e^t}}}{{1 + {e^t}}}dt + \int \limits_0^1 \frac{{{t^2}dt}}{{{e^t} + 1}}\\
= \int \limits_0^1 \frac{{{t^2}{e^t} + {t^2}}}{{{e^t} + 1}}dt = \int \limits_0^1 \frac{{{t^2}\left( {{e^t} + 1} \right)}}{{{e^t} + 1}}dt\\
= \int \limits_0^1 {t^2}dt
\end{array}\)
Vậy \(\int \limits_{ - 1}^1 \frac{{{t^2}dt}}{{{e^t} + 1}} = \int \limits_0^1 {t^2}dt\)
c) Sai.
Đặt \(\sin x = t \Rightarrow \cos xdx = dt\)
\( \Rightarrow \int \limits_0^1 {\sin ^3}s\cos xdx = \int \limits_0^{\frac{\pi }{2}} {t^3}dt \ne \int \limits_0^1 {t^3}dt\)
Vậy c sai.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.46 trang 181 SBT Toán 12
Bài tập 3.47 trang 181 SBT Toán 12
Bài tập 3.49 trang 182 SBT Toán 12
Bài tập 3.50 trang 182 SBT Toán 12
Bài tập 3.51 trang 182 SBT Toán 12
Bài tập 3.52 trang 182 SBT Toán 12
Bài tập 3.53 trang 183 SBT Toán 12
Bài tập 3.54 trang 183 SBT Toán 12
Bài tập 3.55 trang 183 SBT Toán 12
Bài tập 3.56 trang 183 SBT Toán 12
Bài tập 3.67 trang 183 SBT Toán 12
Bài tập 3.58 trang 184 SBT Toán 12
-


A. \(\int {\cos 3x{\rm{d}}x = 3\sin 3x + C} \) .
B. \(\int {\cos 3x{\rm{d}}x = \frac{{\sin 3x}}{3} + C} \) .
C. \(\int {\cos 3x{\rm{d}}x = - \frac{{\sin 3x}}{3} + C} \) .
D. \(\int {\cos 3x{\rm{d}}x = \sin 3x + C} \) .
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của hàm số (fleft( x ight) = {x^2} + frac{2}{{{x^2}}})?
bởi Nguyễn Thanh Trà
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của hàm số (fleft( x ight) = cos 2x)
bởi Lê Gia Bảo
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời -


Tính \(\int\limits_0^1 {\frac{1}{{{x^2} - x + 1}}dx} \)?
bởi Gia Bảo
 10/05/2020
10/05/2020
tính tích phân
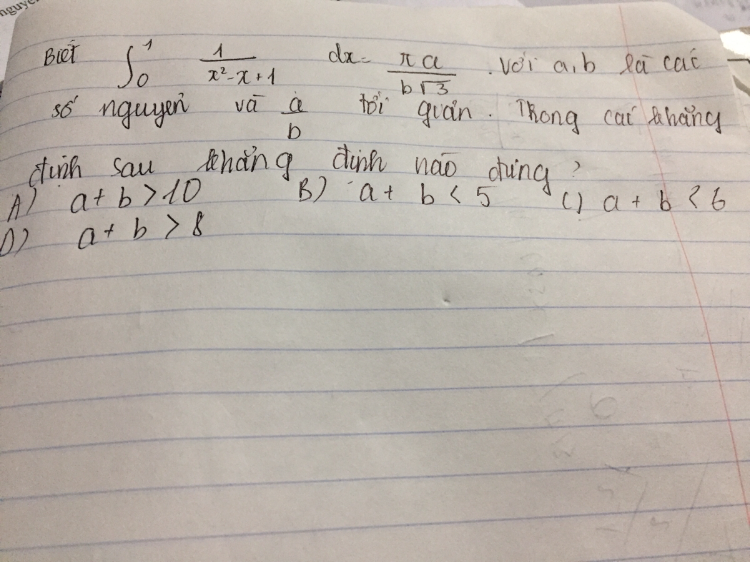 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -
ADMICRO


Tính các tích phân sau?
bởi vu vu
 08/05/2020
Tính các tích phân sau(bằng tự luận).
08/05/2020
Tính các tích phân sau(bằng tự luận).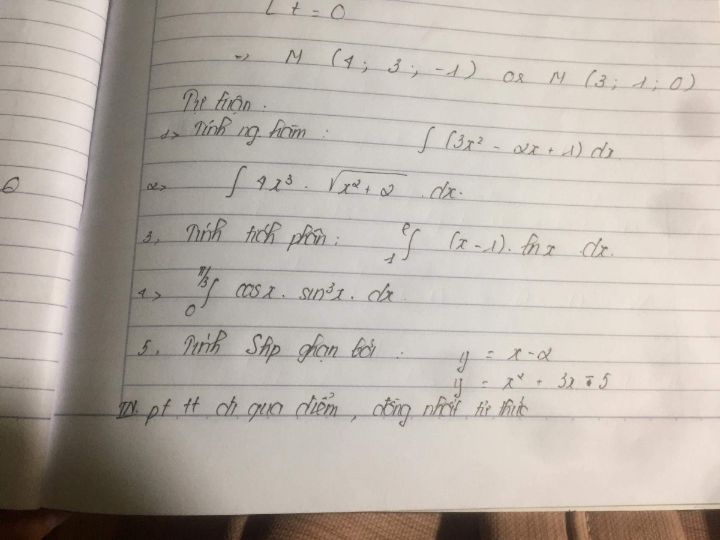 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


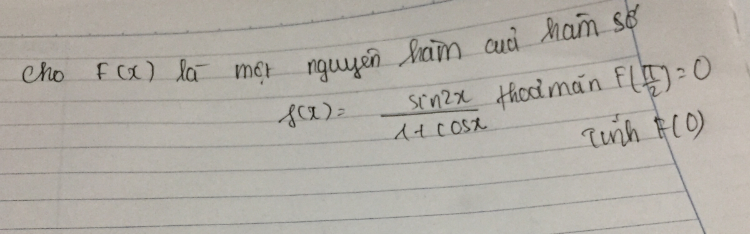 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tích phân từ 0 đến 1 của x(x+3)^4dx
bởi Nguyễn Trí Thành
 19/04/2020
Tính tích phân
19/04/2020
Tính tích phân Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời



