Bài tập 3.51 trang 182 SBT Toán 12
Tìm khẳng định sai trong các khẳng định sau:
A. \(\int \limits_0^1 \sin \left( {1 - x} \right)dx = \mathop \smallint \limits_0^1 \sin xdx\)
B. \(\int \limits_0^\pi \sin \frac{x}{2}dx = 2\mathop \smallint \limits_0^{\frac{\pi }{2}} \sin xdx\)
C. \(\int \limits_0^1 {\left( {1 + x} \right)^x}dx = 0\)
D. \(\int \limits_{ - 1}^1 {x^{2007}}\left( {1 + x} \right)dx = \frac{2}{{2009}}\)
Hướng dẫn giải chi tiết
Đáp án A:
Đặt \(t = 1 - x \Rightarrow dt = - dx\)
\( \Rightarrow \int \limits_0^1 \sin \left( {1 - x} \right)dx = \int \limits_1^0 \sin t\left( { - dt} \right)\)
\(\int \limits_0^1 \sin \left( {1 - x} \right)dx = \int \limits_0^1 \sin tdt = \int \limits_0^1 \sin xdx\) n
Nên A đúng.
Đáp án B:
Ta có:
\(\int\limits_2^\pi {\sin \frac{x}{2}dx = - 2\left. {\cos \frac{x}{2}} \right|_0^\pi = 2} \)
\(2\int\limits_2^{\frac{\pi }{2}} {\sin xdx = - 2\left. {\cos x} \right|_0^{\frac{\pi }{2}} = 2} \)
Nên \(\int \limits_0^\pi \sin \frac{x}{2}dx = 2\int \limits_0^{\frac{\pi }{2}} \sin xdx\) h
Hay B đúng.
Đáp án D:
\(\begin{array}{l}
\int \limits_{ - 1}^1 {x^{2007}}\left( {1 + x} \right)dx\\
= \int \limits_{ - 1}^1 \left( {{x^{2007}} + {x^{2008}}} \right)dx\\
= \left. {\left( {\frac{{{x^{2008}}}}{{2008}} + \frac{{{x^{2009}}}}{{2009}}} \right)} \right|_{ - 1}^1\\
= \frac{1}{{2008}} + \frac{1}{{2009}} - \frac{1}{{2008}} + \frac{1}{{2009}}\\
= \frac{2}{{2009}}
\end{array}\)
Hay D đúng.
Chọn C.
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.49 trang 182 SBT Toán 12
Bài tập 3.50 trang 182 SBT Toán 12
Bài tập 3.52 trang 182 SBT Toán 12
Bài tập 3.53 trang 183 SBT Toán 12
Bài tập 3.54 trang 183 SBT Toán 12
Bài tập 3.55 trang 183 SBT Toán 12
Bài tập 3.56 trang 183 SBT Toán 12
Bài tập 3.67 trang 183 SBT Toán 12
Bài tập 3.58 trang 184 SBT Toán 12
-


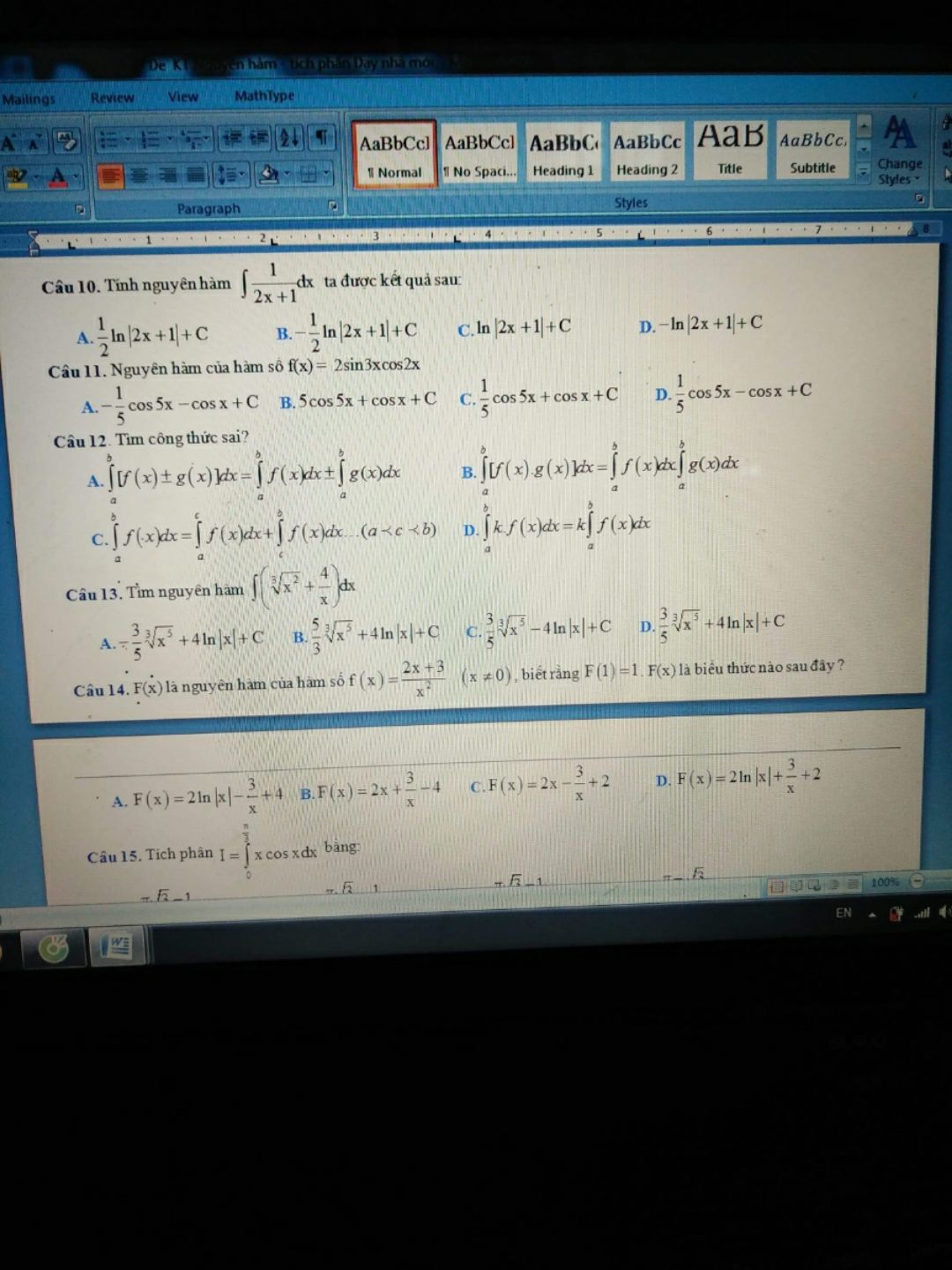
Tìm nguyên hàm (căn bậc 3 của x^2+4/x)dx
bởi Luân Trương Nhất
 17/02/2020
17/02/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


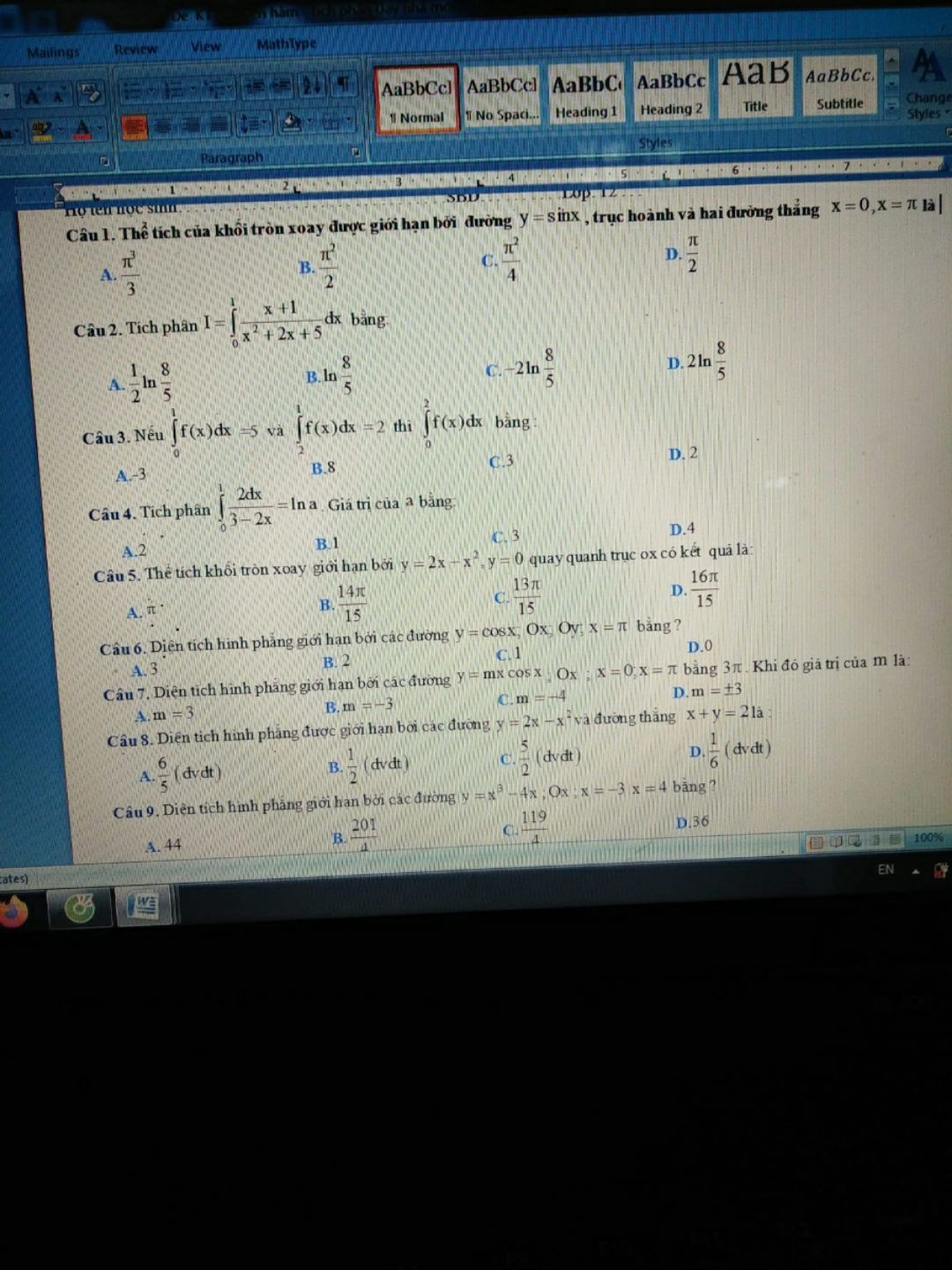
Diện tích hình phẳng giới hạn bởi các đường y=cosx, Ox, Oy, x=pi bằng?
bởi Luân Trương Nhất
 17/02/2020
17/02/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính giá trị của tích phân I=tích phân từ 0 đến 2 f(x)dx biết f(x) liên tục trên [0;2]
bởi hoàng trí bảo
 17/02/2020
Câu 37 ạ
17/02/2020
Câu 37 ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính diện tích hình phẳng được đánh dấu trên hình bên
bởi pino
 16/02/2020
Câu 25
16/02/2020
Câu 25 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -
ADMICRO


Tìm nguyên hàm f(x)=1+sin3x
bởi Cao Thị Huỳnh My
 11/02/2020
Tìm nguyên hàm f(x)=1 sin3xTheo dõi (0) 3 Trả lời
11/02/2020
Tìm nguyên hàm f(x)=1 sin3xTheo dõi (0) 3 Trả lời -


Tìm nguyên hàm của x(2cos^2 x-1)dx
bởi Huỳnh Ngọc
 10/02/2020
10/02/2020
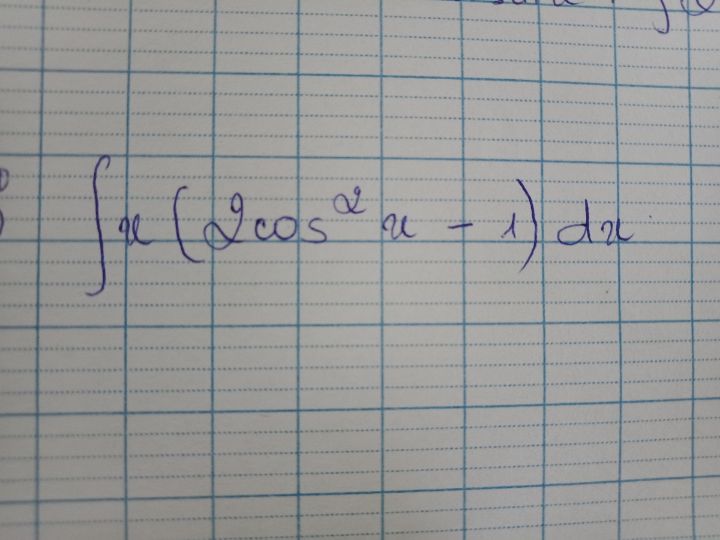 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tích phân từ 0 đến pi/2 của cos^5 x/(1+sin x)dx
bởi Huỳnh Ngọc
 10/02/2020
10/02/2020
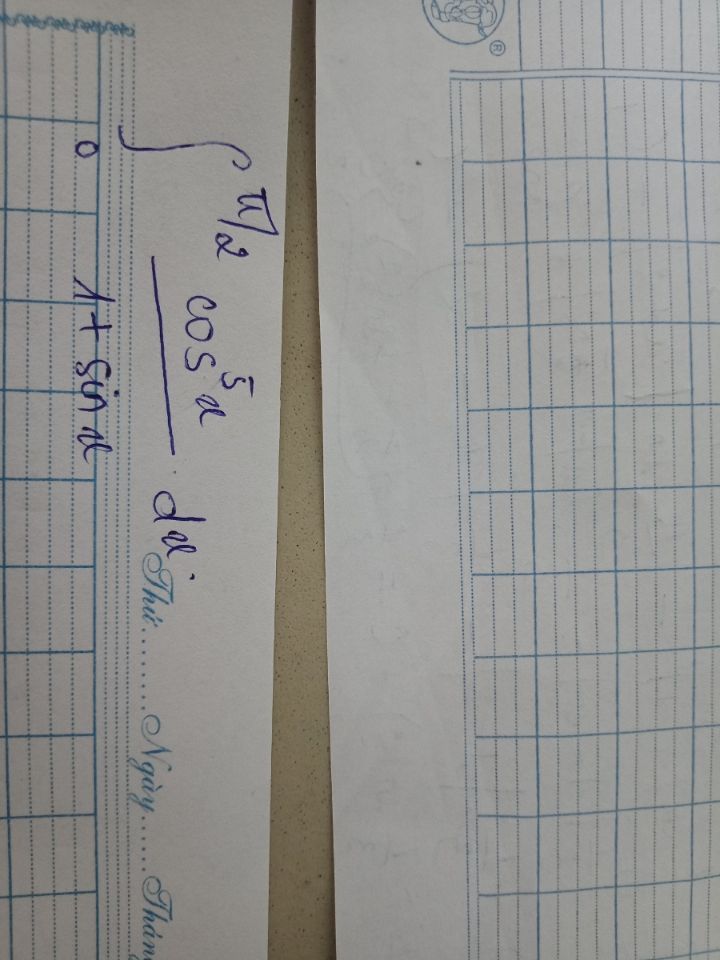 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời



