Bài tập 50 trang 176 SGK Toán 12 NC
Tính các tích phân sau:
\(\begin{array}{l}
a)\int_0^{\frac{\pi }{2}} {{x^2}sin2xdx} \\
b)\int_1^2 {x(2{x^2} + 1)dx} \\
c)\int_2^3 {(x - 1){e^{{x^2} - 2x}}dx}
\end{array}\)
Hướng dẫn giải chi tiết
a) Đặt \(\left\{ \begin{array}{l}
u = {x^2}\\
dv = \sin 2xdx
\end{array} \right. \)
\(\Rightarrow \left\{ \begin{array}{l}
du = 2xdx\\
v = - \frac{1}{2}\cos 2x
\end{array} \right.\)
Do đó:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\int_0^{\frac{\pi }{2}} {{x^2}\sin 2xdx} \\
= \left. { - \frac{1}{2}{x^2}\cos 2x} \right|_0^{\frac{\pi }{2}} + \int_0^{\frac{\pi }{2}} {{x^2}\cos 2xdx}
\end{array}\\
{ = \frac{{{\pi ^2}}}{8} + \int_0^{\frac{\pi }{2}} {x\cos 2xdx\left( 1 \right)} }
\end{array}\)
Đặt \(\left\{ \begin{array}{l}
u = x\\
dv = \cos 2xdx
\end{array} \right. \)
\(\Rightarrow \left\{ \begin{array}{l}
du = dx\\
v = \frac{1}{2}\sin 2x
\end{array} \right.\)
Do đó:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\int_0^{\frac{\pi }{2}} {x\cos 2xxdx} \\
= \left. {\frac{1}{2}x\sin 2x} \right|_0^{\frac{\pi }{2}} - \frac{1}{2}\int_0^{\frac{\pi }{2}} {\sin 2xdx}
\end{array}\\
{ = \left. {\frac{1}{4}\cos 2x} \right|_0^{\frac{\pi }{2}} = - \frac{1}{2}\left( 2 \right)}
\end{array}\)
Thay (2) vào (1) ta được:
\(\int_0^{\frac{\pi }{2}} {{x^2}\sin 2xdx} = \frac{{{\pi ^2}}}{8} - \frac{1}{2}\)
b) Đặt \(u = 2{x^2} + 1\)
\(\Rightarrow du = 4xdx \Rightarrow xdx = \frac{{du}}{4}\)
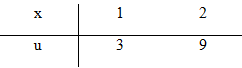
\(\begin{array}{l}
\int_1^2 {x(2{x^2} + 1)dx} \\
= \frac{1}{4}\int_3^9 {udu} = \left. {\frac{1}{8}{u^2}} \right|_3^9 = 9
\end{array}\)
c) Đặt \(u = {x^2} - 2x \)
\(\Rightarrow du = 2(x - 1)dx \Rightarrow (x - 1)dx = \frac{{du}}{2}\)
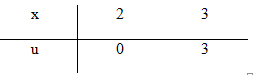
\(\begin{array}{l}
\int_2^3 {(x - 1){e^{{x^2} - 2x}}dx} \\
= \frac{1}{2}\int_0^3 {{e^u}du} \\
= \left. {\frac{1}{2}{e^u}} \right|_0^3 = \frac{1}{2}({e^3} - 1)
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 48 trang 176 SGK Toán 12 NC
Bài tập 49 trang 176 SGK Toán 12 NC
Bài tập 51 trang 176 SGK Toán 12 NC
Bài tập 52 trang 177 SGK Toán 12 NC
Bài tập 53 trang 177 SGK Toán 12 NC
Bài tập 54 trang 177 SGK Toán 12 NC
Bài tập 55 trang 177 SGK Toán 12 NC
Bài tập 56 trang 177 SGK Toán 12 NC
Bài tập 57 trang 177 SGK Toán 12 NC
Bài tập 58 trang 177 SGK Toán 12 NC
Bài tập 59 trang 177 SGK Toán 12 NC
Bài tập 60 trang 178 SGK Toán 12 NC
Bài tập 61 trang 178 SGK Toán 12 NC
Bài tập 62 trang 178 SGK Toán 12 NC
Bài tập 63 trang 178 SGK Toán 12 NC
Bài tập 64 trang 178 SGK Toán 12 NC
Bài tập 65 trang 178 SGK Toán 12 NC
Bài tập 66 trang 179 SGK Toán 12 NC
Bài tập 67 trang 179 SGK Toán 12 NC
Bài tập 3.43 trang 180 SBT Toán 12
Bài tập 3.44 trang 180 SBT Toán 12
Bài tập 3.45 trang 181 SBT Toán 12
Bài tập 3.46 trang 181 SBT Toán 12
Bài tập 3.47 trang 181 SBT Toán 12
Bài tập 3.48 trang 181 SBT Toán 12
Bài tập 3.49 trang 182 SBT Toán 12
Bài tập 3.50 trang 182 SBT Toán 12
Bài tập 3.51 trang 182 SBT Toán 12
Bài tập 3.52 trang 182 SBT Toán 12
Bài tập 3.53 trang 183 SBT Toán 12
Bài tập 3.54 trang 183 SBT Toán 12
Bài tập 3.55 trang 183 SBT Toán 12
Bài tập 3.56 trang 183 SBT Toán 12
Bài tập 3.67 trang 183 SBT Toán 12
Bài tập 3.58 trang 184 SBT Toán 12
-


Tính nguyên hàm sau: \(\int {{{\left( {5x + 3} \right)}^3}\,dx} \) ta được kết quả:
bởi Bao Chau
 06/05/2021
06/05/2021
A. \(\dfrac{1}{{20}}{\left( {5x + 3} \right)^4} + C\).
B. \(\dfrac{1}{{20}}{\left( {5x + 3} \right)^4}\).
C. \(\dfrac{1}{4}{\left( {5x + 3} \right)^4} + C\).
D. \(\dfrac{1}{5}{\left( {5x + 3} \right)^4} + C\).
Theo dõi (0) 1 Trả lời -


Cho biết hàm số nào dưới đây không là nguyên hàm của \(f(x) = \dfrac{{2x\left( {x + 3} \right)}}{{{{\left( {x + 1} \right)}^2}}}\) ?
bởi Nguyễn Thanh Thảo
 05/05/2021
05/05/2021
A. \(2\ln |x + 1| + \dfrac{{2{x^2} + 2x + 4}}{{x + 1}}\).
B. \(\ln \left( {x + 1} \right) + \dfrac{{2{x^2} + 2x + 4}}{{x + 1}}\).
C. \(\ln {\left( {x + 1} \right)^2} + \dfrac{{2{x^2} + 3x + 5}}{{x + 1}}\).
D. \(\dfrac{{2{x^2} + 3x + 5}}{{x + 1}} + \ln {e^2}{\left( {x + 1} \right)^2}\).
Theo dõi (0) 1 Trả lời -


Đặt \(F(x) = \int\limits_1^x {t\,dt} \). Khi đó F’(x) là hàm số nào bên dưới đây?
bởi Nguyễn Thanh Thảo
 05/05/2021
05/05/2021
A . F’(x) = x.
B. F’(x) = 1.
C. F’(x) = x – 1.
D. F’(x) = \(\dfrac{{{x^2}}}{2} - \dfrac{1}{2}\).
Theo dõi (0) 1 Trả lời -


A. \(I = \sin \left( {4x + 2} \right) + C\).
B. \(I = - \sin \left( {4x + 3} \right) + C\).
C. \(I = \dfrac{1}{4}\sin \left( {4x + 3} \right) + C\).
D. \(I = 4\sin \left( {4x + 3} \right) + C\).
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho biết thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y = \tan x,\,\,y = 0,\,\,x = \dfrac{\pi }{3}\) quanh Ox là:
bởi Hoa Hong
 06/05/2021
06/05/2021
A. \(\sqrt 3 - \dfrac{\pi }{3}\)
B. \(\dfrac{\pi }{3} - 3\)
C. \(\dfrac{{{\pi ^2}}}{3} - \pi \sqrt 3 \)
D. \(\pi \sqrt 3 - \dfrac{{{\pi ^2}}}{3}\).
Theo dõi (0) 1 Trả lời -


A. \(I = \ln |x - 3| - \dfrac{{16}}{{x - 3}} + C\).
B. \(I = \dfrac{1}{5}\ln |x - 3| - \dfrac{{16}}{{x - 3}} + C\).
C. \(I = \ln |x - 3| + \dfrac{{16}}{{x - 3}} + C\).
D. \(I = 5\ln |x - 3| - \dfrac{{16}}{{x - 3}} + C\).
Theo dõi (0) 1 Trả lời -


A. \(\int {\dfrac{{dx}}{{6x - 2}} = 6\ln |6x - 2| + C} \).
B. \(\int {\dfrac{{dx}}{{6x - 2}} = \dfrac{1}{6}\ln |6x - 2| + C} \).
C. \(\int {\dfrac{{dx}}{{6x - 2}} = \dfrac{1}{2}\ln |6x - 2| + C} \).
D. \(\int {\dfrac{{dx}}{{6x - 2}} = \ln |6x - 2| + C} \).
Theo dõi (0) 1 Trả lời




