Giải bài 3 tr 51 sách GK Toán Hình lớp 12
Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, có SA vuông góc với (ABC) và có SA = a, AB = b và AC = c. Mặt cầu đi qua các đỉnh A,B,C,S có bán kính r bằng
(A) \(\frac{2(a+b+c)}{3}\) (B) \(2\sqrt{a^2+b^2+c^2}\)
(C) \(\frac{1}{2}\sqrt{a^2+b^2+c^2}\) (D) \(\sqrt{a^2+b^2+c^2}\)
Gợi ý trả lời bài 3
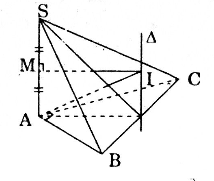
Gọi O là trung điểm của BC ⇒ O là tâm đường tròn ngoại tiếp tam giác ABC. Đường thẳng \(\Delta\) là trục của đường tròn tâm O.
Gọi I là giao điểm của mặt phẳng trung trực của SA và \(\Delta\). Khi đó I là tâm của mặt cầu đi qua A, B, C, S và r = IA.
Bán kính mặt cầu này là
\(r=IA=\sqrt{OA^2+IO^2} =\sqrt{\left (\frac{BC}{2} \right )^2+\left (\frac{SA}{2} \right )^2}\)
\(= \frac{1}{2}\sqrt{a^2+b^2+c^2}\)
⇒ Chọn đáp án C
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1 trang 51 SGK Hình học 12
Bài tập 2 trang 51 SGK Hình học 12
Bài tập 4 trang 51 SGK Hình học 12
Bài tập 5 trang 51 SGK Hình học 12
Bài tập 6 trang 51 SGK Hình học 12
Bài tập 7 trang 52 SGK Hình học 12
Bài tập 8 trang 52 SGK Hình học 12
Bài tập 9 trang 52 SGK Hình học 12
Bài tập 10 trang 52 SGK Hình học 12
Bài tập 11 trang 53 SGK Hình học 12
Bài tập 12 trang 53 SGK Hình học 12
Bài tập 13 trang 53 SGK Hình học 12
Bài tập 14 trang 53 SGK Hình học 12
Bài tập 15 trang 54 SGK Hình học 12
Bài tập 16 trang 54 SGK Hình học 12
Bài tập 17 trang 54 SGK Hình học 12
Bài tập 18 trang 54 SGK Hình học 12
Bài tập 2.25 trang 62 SBT Hình học 12
Bài tập 2.26 trang 62 SBT Hình học 12
Bài tập 2.27 trang 62 SBT Hình học 12
Bài tập 2.28 trang 62 SBT Hình học 12
Bài tập 2.29 trang 63 SBT Hình học 12
Bài tập 2.30 trang 63 SBT Hình học 12
Bài tập 2.31 trang 63 SBT Hình học 12
Bài tập 2.32 trang 63 SBT Hình học 12
Bài tập 2.33 trang 64 SBT Hình học 12
Bài tập 2.34 trang 64 SBT Hình học 12
Bài tập 2.35 trang 64 SBT Hình học 12
Bài tập 2.36 trang 64 SBT Hình học 12
Bài tập 2.37 trang 64 SBT Hình học 12
Bài tập 3.38 trang 64 SBT Hình học 12
Bài tập 2.39 trang 65 SBT Hình học 12
Bài tập 2.40 trang 65 SBT Hình học 12
Bài tập 2.41 trang 65 SBT Hình học 12
Bài tập 2.42 trang 65 SBT Hình học 12
Bài tập 2.43 trang 65 SBT Hình học 12
Bài tập 2.44 trang 66 SBT Hình học 12
Bài tập 2.45 trang 66 SBT Hình học 12
Bài tập 2.46 trang 66 SBT Hình học 12
Bài tập 2.47 trang 66 SBT Hình học 12
Bài tập 2.48 trang 66 SBT Hình học 12
Bài tập 2.49 trang 66 SBT Hình học 12
Bài tập 1 trang 63 SGK Hình học 12 NC
Bài tập 2 trang 63 SGK Hình học 12 NC
Bài tập 3 trang 63 SGK Hình học 12 NC
Bài tập 4 trang 63 SGK Hình học 12 NC
Bài tập 5 trang 63 SGK Hình học 12 NC
Bài tập 6 trang 63 SGK Hình học 12 NC
Bài tập 1 trang 63 SGK Hình học 12 NC
Bài tập 2 trang 64 SGK Hình học 12 NC
Bài tập 3 trang 64 SGK Hình học 12 NC
Bài tập 4 trang 64 SGK Hình học 12 NC
Bài tập 5 trang 64 SGK Hình học 12 NC
Bài tập 6 trang 65 SGK Hình học 12 NC
Bài tập 7 trang 65 SGK Hình học 12 NC
Bài tập 8 trang 65 SGK Hình học 12 NC
Bài tập 9 trang 65 SGK Hình học 12 NC
Bài tập 10 trang 65 SGK Hình học 12 NC
Bài tập 11 trang 66 SGK Hình học 12 NC
Bài tập 12 trang 66 SGK Hình học 12 NC
Bài tập 13 trang 66 SGK Hình học 12 NC
Bài tập 14 trang 66 SGK Hình học 12 NC
Bài tập 15 trang 66 SGK Hình học 12 NC
Bài tập 16 trang 67 SGK Hình học 12 NC
Bài tập 17 trang 67 SGK Hình học 12 NC
Bài tập 18 trang 67 SGK Hình học 12 NC
Bài tập 19 trang 67 SGK Hình học 12 NC
Bài tập 20 trang 67 SGK Hình học 12 NC
Bài tập 21 trang 67 SGK Hình học 12 NC
Bài tập 22 trang 68 SGK Hình học 12 NC
Bài tập 23 trang 68 SGK Hình học 12 NC
Bài tập 24 trang 68 SGK Hình học 12 NC
-


Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh \(2a\) có diện tích xung quanh là \({S_1}\) và một mặt cầu có đường kính bằng chiều cao hình nón có diện tích \({S_2}\). Khi đó hệ thức giữa \({S_1}\) và \({S_2}\) là đáp án?
bởi My Hien
 07/06/2021
07/06/2021
A. \({S_1} = {S_2}\)
B. \({S_1} = 4{S_2}\)
C. \({S_2} = 2{S_1}\)
D. \(2{S_2} = 3{S_1}\)
Theo dõi (0) 1 Trả lời -


Tam giác \(ABC\) vuông tại \(A\) có \(BC = 2a\) và \(\widehat B = {30^0}\). Quay tam giác vuông này quanh trục \(AB\), ta được một hình nón đỉnh \(B\). Gọi \({S_1}\) là diện tích toàn phân của hình nón đó và \({S_2}\) là diện tích mặt cầu có đường kính \(AB\). Khi đó, tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\) là:
bởi Trieu Tien
 07/06/2021
07/06/2021
A. \(1\)
B. \(\dfrac{1}{2}\)
C. \(\dfrac{2}{3}\)
D. \(\dfrac{3}{2}\)
Theo dõi (0) 1 Trả lời -


Mặt cầu \(S\left( {O;R} \right)\) và mặt phẳng \(\left( \alpha \right)\). Gọi \(d\) là khoảng cách từ \(O\) tới \(\left( \alpha \right)\). Khi \(d < R\) thì mặt phẳng \(\left( \alpha \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là đường tròn có bán kính bằng:
bởi Lê Minh
 07/06/2021
07/06/2021
A. \(\sqrt {{R^2} + {d^2}} \)
B. \(\sqrt {{R^2} - {d^2}} \)
C. \(\sqrt {Rd} \)
D. \(\sqrt {{R^2} - 2{d^2}} \)
Theo dõi (0) 1 Trả lời -


Cho một hình hộp chữ nhật có ba kích thước lần lượt là \(a,b,c\). Gọi \(\left( S \right)\) là mặt cầu đi qua \(8\) đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu \(\left( S \right)\) theo \(a,b,c\) là:
bởi Mai Linh
 06/06/2021
06/06/2021
A. \(\pi \left( {{a^2} + {b^2} + {c^2}} \right)\)
B. \(2\pi \left( {{a^2} + {b^2} + {c^2}} \right)\)
C. \(4\pi \left( {{a^2} + {b^2} + {c^2}} \right)\)
D. \(\dfrac{\pi }{2}\left( {{a^2} + {b^2} + {c^2}} \right)\)
Theo dõi (0) 1 Trả lời


