Giải bài 16 tr 54 sách GK Toán Hình lớp 12
Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính quả bóng bàn. Gọi S1 là tổng diện tích của ba quả bóng bàn, S2 là diện tích xung quanh của hình trụ. Tỉ số S1/S2 bằng:
(A) 1
(B) 2
(C) 1,5
(D) 1,2
Gợi ý trả lời bài 16
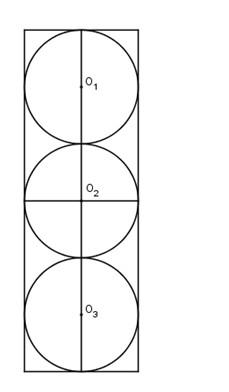
Gọi bán kính của quả cầu là \(r\) thì \(r\) cũng là bán kính đáy của hình trụ.
Chiều cao của hình trụ là \(h=3.2r=6r\)
Diện tích ba quả bóng bàn là: \({S_1} = 3.4\pi {r^2} = 12\pi {r^2}\)
Diện tích xung quanh của hình trụ là: \({S_2} =2\pi r.6r= 12\pi {r^2}\)
Vậy \(\dfrac{{{S_1}}}{{{S_2}}} = 1\).
Chọn (A).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 14 trang 53 SGK Hình học 12
Bài tập 15 trang 54 SGK Hình học 12
Bài tập 17 trang 54 SGK Hình học 12
Bài tập 18 trang 54 SGK Hình học 12
Bài tập 2.25 trang 62 SBT Hình học 12
Bài tập 2.26 trang 62 SBT Hình học 12
Bài tập 2.27 trang 62 SBT Hình học 12
Bài tập 2.28 trang 62 SBT Hình học 12
Bài tập 2.29 trang 63 SBT Hình học 12
Bài tập 2.30 trang 63 SBT Hình học 12
Bài tập 2.31 trang 63 SBT Hình học 12
Bài tập 2.32 trang 63 SBT Hình học 12
Bài tập 2.33 trang 64 SBT Hình học 12
Bài tập 2.34 trang 64 SBT Hình học 12
Bài tập 2.35 trang 64 SBT Hình học 12
Bài tập 2.36 trang 64 SBT Hình học 12
Bài tập 2.37 trang 64 SBT Hình học 12
Bài tập 3.38 trang 64 SBT Hình học 12
Bài tập 2.39 trang 65 SBT Hình học 12
Bài tập 2.40 trang 65 SBT Hình học 12
Bài tập 2.41 trang 65 SBT Hình học 12
Bài tập 2.42 trang 65 SBT Hình học 12
Bài tập 2.43 trang 65 SBT Hình học 12
Bài tập 2.44 trang 66 SBT Hình học 12
Bài tập 2.45 trang 66 SBT Hình học 12
Bài tập 2.46 trang 66 SBT Hình học 12
Bài tập 2.47 trang 66 SBT Hình học 12
Bài tập 2.48 trang 66 SBT Hình học 12
Bài tập 2.49 trang 66 SBT Hình học 12
Bài tập 1 trang 63 SGK Hình học 12 NC
Bài tập 2 trang 63 SGK Hình học 12 NC
Bài tập 3 trang 63 SGK Hình học 12 NC
Bài tập 4 trang 63 SGK Hình học 12 NC
Bài tập 5 trang 63 SGK Hình học 12 NC
Bài tập 6 trang 63 SGK Hình học 12 NC
Bài tập 1 trang 63 SGK Hình học 12 NC
Bài tập 2 trang 64 SGK Hình học 12 NC
Bài tập 3 trang 64 SGK Hình học 12 NC
Bài tập 4 trang 64 SGK Hình học 12 NC
Bài tập 5 trang 64 SGK Hình học 12 NC
Bài tập 6 trang 65 SGK Hình học 12 NC
Bài tập 7 trang 65 SGK Hình học 12 NC
Bài tập 8 trang 65 SGK Hình học 12 NC
Bài tập 9 trang 65 SGK Hình học 12 NC
Bài tập 10 trang 65 SGK Hình học 12 NC
Bài tập 11 trang 66 SGK Hình học 12 NC
Bài tập 12 trang 66 SGK Hình học 12 NC
Bài tập 13 trang 66 SGK Hình học 12 NC
Bài tập 14 trang 66 SGK Hình học 12 NC
Bài tập 15 trang 66 SGK Hình học 12 NC
Bài tập 16 trang 67 SGK Hình học 12 NC
Bài tập 17 trang 67 SGK Hình học 12 NC
Bài tập 18 trang 67 SGK Hình học 12 NC
Bài tập 19 trang 67 SGK Hình học 12 NC
Bài tập 20 trang 67 SGK Hình học 12 NC
Bài tập 21 trang 67 SGK Hình học 12 NC
Bài tập 22 trang 68 SGK Hình học 12 NC
Bài tập 23 trang 68 SGK Hình học 12 NC
Bài tập 24 trang 68 SGK Hình học 12 NC
-


Xét mệnh đề sau đúng hay sai: Mọi tứ diện luôn có cạnh bên bằng nhau đều có mặt cầu ngoại tiếp.
bởi Hoai Hoai
 06/06/2021
06/06/2021
Xét mệnh đề sau đúng hay sai: Mọi tứ diện luôn có cạnh bên bằng nhau đều có mặt cầu ngoại tiếp.
Theo dõi (0) 1 Trả lời -


Xét mệnh đề sau đúng hay sai: Mặt cầu, khối cầu đều có vô số mặt phẳng đối xứng.
bởi Kim Ngan
 06/06/2021
06/06/2021
Xét mệnh đề sau đúng hay sai: Mặt cầu, khối cầu đều có vô số mặt phẳng đối xứng.
Theo dõi (0) 1 Trả lời -


Cho tam giác \(ABC\) vuông tại \(A, AB = c, AB = b\). Hãy tính thể tích của khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi quay quanh đường thẳng \(BC\).
bởi Nhat nheo
 06/06/2021
06/06/2021
Cho tam giác \(ABC\) vuông tại \(A, AB = c, AB = b\). Hãy tính thể tích của khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi quay quanh đường thẳng \(BC\).
Theo dõi (0) 1 Trả lời -


Một mặt cầu gọi là nội tiếp hình nón nếu nó tiếp xúc với mặt đáy của hình nón và tiếp xúc với mọi đường sinh của hình nón. Khi đó hình nón được gọi là ngoại tiếp mặt cầu. Chứng minh mọi hình nón đều có một mặt cầu nội tiếp duy nhất.
bởi Nguyễn Thanh Thảo
 07/06/2021
07/06/2021
Một mặt cầu gọi là nội tiếp hình nón nếu nó tiếp xúc với mặt đáy của hình nón và tiếp xúc với mọi đường sinh của hình nón. Khi đó hình nón được gọi là ngoại tiếp mặt cầu. Chứng minh mọi hình nón đều có một mặt cầu nội tiếp duy nhất.
Theo dõi (0) 1 Trả lời


