Bài tập 6 trang 63 SGK Hình học 12 NC
Một hình thang cân ABCD có các cạnh đáy AB = 2a, BD = 4a, cạnh bên AD = BC = 3a. Hãy tính thể tích và diện tích toàn phần của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó.
Hướng dẫn giải chi tiết
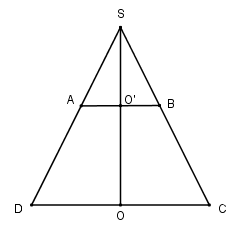
Gọi S là giao điểm của hai cạnh bên AD và BC của hình thang. Đường cao SO của tam giác cân SCD là trục đối xứng của hình thang, do đó SO cắt AB tại trung điểm O′ của AB.
Khi quay quanh SO, tam giác SCD sinh ra khối nón (N1) có thể tích V1, tam giác SAB sinh ra khối nón (N2) có thể tích V2, còn hình thang ABCD sinh ra một khối tròn xoay (H) có thể tích V = V1 − V2.
Vì \(AB = \frac{1}{2}CD\) nên AB là đường trung bình của tam giác SCD nên SB = BC = 3a.
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
SO\prime = \sqrt {S{B^2} - O\prime {B^2}} \\
= \sqrt {9{a^2} - {a^2}} = 2\sqrt 2 a
\end{array}\\
{SO = 2SO\prime = 4\sqrt 2 a}\\
\begin{array}{l}
V = {V_1} - {V_2} = \frac{1}{3}\pi O{C^2}.SO - \frac{1}{3}\pi O\prime {B^2}.SO\prime \\
= \frac{1}{3}\pi 4{a^2}.SO - \frac{1}{3}\pi {a^2}SO\prime
\end{array}\\
\begin{array}{l}
= \frac{1}{4}\pi {a^2}(4SO - SO\prime )\\
= \frac{1}{3}\pi {a^2}(16\sqrt 2 a - 2\sqrt 2 a) = \frac{{14\sqrt 2 }}{3}\pi {a^3}
\end{array}
\end{array}\)
Diện tích xung quanh của khối tròn xoay (H) là
\(\begin{array}{*{20}{l}}
\begin{array}{l}
{S_{xq}} = {S_1} - {S_2}\\
= \pi OC.SC - \pi O\prime B.SB = 9\pi {a^2}
\end{array}\\
\begin{array}{l}
{S_{tp}} = {S_{xq}} + {S_d}\\
= 9\pi {a^2} + \pi {a^2} + 4\pi {a^2} = 14\pi {a^2}
\end{array}
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 4 trang 63 SGK Hình học 12 NC
Bài tập 5 trang 63 SGK Hình học 12 NC
Bài tập 1 trang 63 SGK Hình học 12 NC
Bài tập 2 trang 64 SGK Hình học 12 NC
Bài tập 3 trang 64 SGK Hình học 12 NC
Bài tập 4 trang 64 SGK Hình học 12 NC
Bài tập 5 trang 64 SGK Hình học 12 NC
Bài tập 6 trang 65 SGK Hình học 12 NC
Bài tập 7 trang 65 SGK Hình học 12 NC
Bài tập 8 trang 65 SGK Hình học 12 NC
Bài tập 9 trang 65 SGK Hình học 12 NC
Bài tập 10 trang 65 SGK Hình học 12 NC
Bài tập 11 trang 66 SGK Hình học 12 NC
Bài tập 12 trang 66 SGK Hình học 12 NC
Bài tập 13 trang 66 SGK Hình học 12 NC
Bài tập 14 trang 66 SGK Hình học 12 NC
Bài tập 15 trang 66 SGK Hình học 12 NC
Bài tập 16 trang 67 SGK Hình học 12 NC
Bài tập 17 trang 67 SGK Hình học 12 NC
Bài tập 18 trang 67 SGK Hình học 12 NC
Bài tập 19 trang 67 SGK Hình học 12 NC
Bài tập 20 trang 67 SGK Hình học 12 NC
Bài tập 21 trang 67 SGK Hình học 12 NC
Bài tập 22 trang 68 SGK Hình học 12 NC
Bài tập 23 trang 68 SGK Hình học 12 NC
Bài tập 24 trang 68 SGK Hình học 12 NC
-


Cho hình lăng trụ tứ giác ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và thể tích bằng 3\({a^3}\). Tính chiều cao h của hình lăng trụ đã cho.
bởi Lê Bảo An
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời -


Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với đáy và AB=a, AC=2a,SA=3a. Tính thể tích khối chóp S.ABC.
bởi Lê Gia Bảo
 24/05/2020
Theo dõi (0) 1 Trả lời
24/05/2020
Theo dõi (0) 1 Trả lời -


Tìm mệnh đề sai:
bởi Nguyễn Thanh Trà
 24/05/2020
24/05/2020
A. Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau
B. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau
C. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau
D. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau
Theo dõi (0) 1 Trả lời -


Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
bởi Nguyễn Sơn Ca
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời





