Bài tập 5 trang 63 SGK Hình học 12 NC

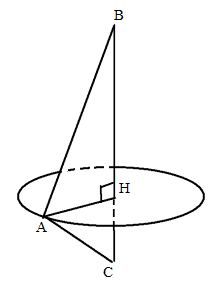
a) Khi quay tam giác ABC quanh AB ta được khối nón có chiều cao AB = c và bán kính đáy AC = b nên có thể tích \({V_1} = \frac{1}{3}\pi c{b^2}\)

Tương tự khi quay tam giác ABC quanh AC ta được khối nón có thể tích \({V_2} = \frac{1}{3}\pi b{c^2}\)

Gọi AH là chiều cao của tam giác ABC. Khi quay tam giác ABC quanh BC ta được hai khối nón sinh bởi hai tam giác ABH và ACH.

Khi đó ta có 

\(\begin{array}{*{20}{l}}
\begin{array}{l}
{V_3} = \frac{1}{3}\pi A{H^2}.BH + \frac{1}{3}\pi A{H^2}.CH\\
 = \frac{1}{3}\pi AH.BC
\end{array}\\
\begin{array}{l}
 = \frac{1}{3}\pi {(bc\sqrt {{b^2} + {c^2}} )^2}\sqrt {{b^2} + {c^2}} \\
 = \frac{1}{3}\frac{{\pi {b^2}{c^2}}}{{\sqrt {{b^2} + {c^2}} }}
\end{array}
\end{array}\)

b) Ta có:

\(\begin{array}{*{20}{l}}
{\frac{1}{{V_3^2}} = \frac{{9({b^2} + {c^2})}}{{\pi {b^4}{c^4}}}}\\
\begin{array}{l}
\frac{1}{{V_1^2}} + \frac{1}{{V_2^2}} = \frac{9}{{\pi {c^2}{b^4}}} + \frac{9}{{\pi {b^2}{c^4}}}\\
 = \frac{{9({b^2} + {c^2})}}{{\pi {b^4}{c^4}}} = \frac{1}{{V_3^2}}
\end{array}
\end{array}\)

-- Mod Toán 12 HỌC247