Giải bài 1.35 tr 21 SBT Toán 12
Tìm giá trị lớn nhất, nhỏ nhất của các hàm số sau:
a) \(y = \frac{x}{{4 + {x^2}}}\) trên khoảng \(( - \infty ; + \infty )\);
b) \(y = \frac{1}{{\cos x}}\) trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\);
Hướng dẫn giải chi tiết
a) \(y\prime = \frac{{4 - {x^2}}}{{{{\left( {4 + {x^2}} \right)}^2}}};y\prime = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 2\\
x = 2
\end{array} \right.\)
Bảng biến thiên:
.png)
Từ đó ta có \(\mathop {\max }\limits_R y = \frac{1}{4};\,\,\mathop {\min }\limits_R y = - \frac{1}{4}.\)
b) \(y' = \frac{{\sin x}}{{{{\cos }^2}x}};y' = 0 \Leftrightarrow x = \pi \)
Bảng biến thiên:
.png)
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là
\(\mathop {\max }\limits_{\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)} y = y\left( \pi \right) = - 1\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1.34 trang 21 SBT Toán 12
Bài tập 1.36 trang 21 SBT Toán 12
Bài tập 1.37 trang 21 SBT Toán 12
Bài tập 1.38 trang 21 SBT Toán 12
Bài tập 1.39 trang 21 SBT Toán 12
Bài tập 1.40 trang 21 SBT Toán 12
Bài tập 1.41 trang 21 SBT Toán 12
Bài tập 1.42 trang 22 SBT Toán 12
Bài tập 1.43 trang 22 SBT Toán 12
Bài tập 1.44 trang 22 SBT Toán 12
Bài tập 1.45 trang 22 SBT Toán 12
Bài tập 1.46 trang 22 SBT Toán 12
Bài tập 16 trang 22 SGK Toán 12 NC
Bài tập 17 trang 22 SGK Toán 12 NC
Bài tập 18 trang 22 SGK Toán 12 NC
Bài tập 19 trang 22 SGK Toán 12 NC
Bài tập 20 trang 22 SGK Toán 12 NC
Bài tập 21 trang 22 SGK Toán 12 NC
Bài tập 22 trang 23 SGK Toán 12 NC
Bài tập 23 trang 23 SGK Toán 12 NC
Bài tập 24 trang 23 SGK Toán 12 NC
Bài tập 25 trang 23 SGK Toán 12 NC
Bài tập 26 trang 23 SGK Toán 12 NC
-


Khu chung cư Royal City có 250 căn hộ cho thuê. Nếu người ta cho thuê x căn hộ thì lợi nhuận hàng tháng, tính theo triệu đồng, được cho bởi: \(P\left( x \right) = - 8{x^2} + 3200x - 80000\). Hỏi lợi nhuận tối đa họ có thể đạt được là bao nhiêu?
bởi Ngoc Nga
 25/01/2021
25/01/2021
A. 150000
B. 220000
C. 292000
D. 250000
Theo dõi (0) 1 Trả lời -


Cho hàm số y = f(x) xác định và liên tục trên R và có bảng biến thiên. Khẳng định nào sau đây là khẳng định đúng?
bởi Mai Rừng
 25/01/2021
25/01/2021
.png)
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.
D. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 1
Theo dõi (0) 1 Trả lời -


A. 11
B. 4
C. 7
D. 2
Theo dõi (0) 1 Trả lời -


Một công ti quản lí chuẩn bị xây dựng một khu chung cư mới. Họ tính toán nếu tòa nhà có x căn hộ thì chi phí bảo trì của tòa nhà là: \(C\left( x \right) = 4000 - 14x + 0,04{x^2}\). Khu đất của họ có thể xây được tòa nhà chứa tối đa 300 căn hộ. Hỏi họ nên xây dựng tòa nhà có bao nhiêu căn hộ để chi phí bảo trì của tòa nhà là nhỏ nhất?
bởi Thùy Trang
 25/01/2021
25/01/2021
A. 150
B.175
C. 300
D.225
Theo dõi (0) 1 Trả lời -
ADMICRO


Tìm giá trị nhỏ nhất của hàm số y= |x+2| trên đoạn [-3;3]?
Mọi người giải giúp mình với ạ, mình cảm ơn ạ
Theo dõi (0) 5 Trả lời -


 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm \(M +m\) trên đoạn [0,2] với M, m lần lượt là GTLN, GTNN của hàm số \(y=\dfrac{3x-1}{x-3}\)?
bởi Đặng Linh
 25/08/2020
25/08/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm giá trị lớn nhất của hàm số \(y=(x-6)\sqrt {x^2+3}\) trên đoạn [1;2]?
bởi Nguyễn Thơm
 23/08/2020
23/08/2020
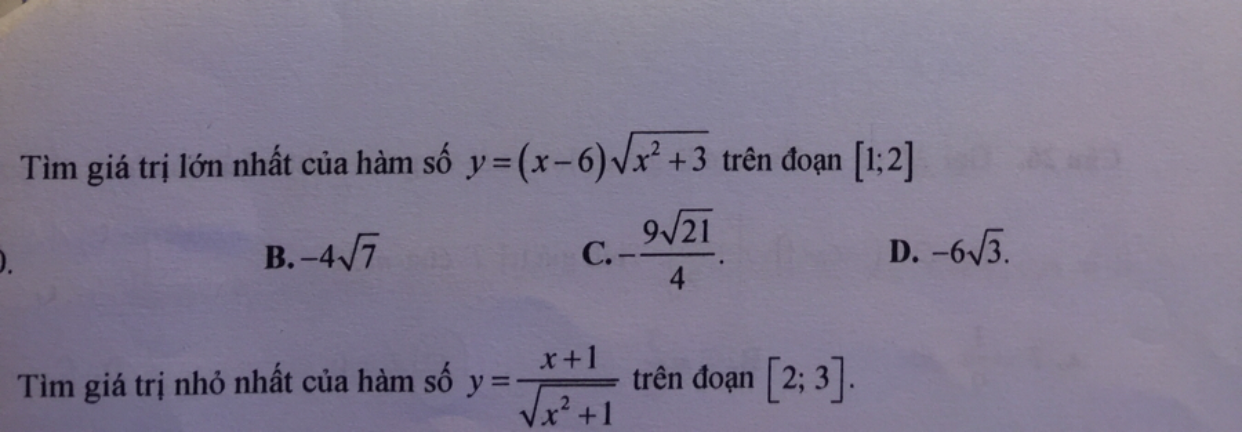 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tìm GTLN,GTNN của hàm số y=1+√9-x^2 và \(y= \cos ^4x+\sin ^4x+\sin x.\cos x+1\)?
bởi Diệu Nguyễn
 18/08/2020
Theo dõi (0) 0 Trả lời
18/08/2020
Theo dõi (0) 0 Trả lời -


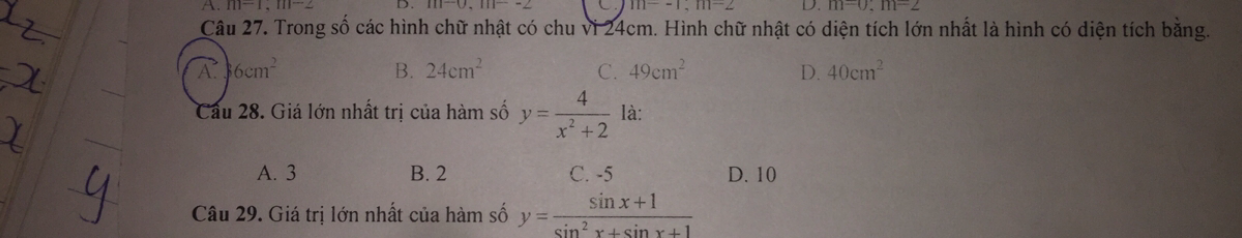 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình \(a^2-2ma+M=0\)?
bởi Nguyễn Thị Hồng Thư
 12/08/2020
12/08/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm giá trị nhỏ nhất của hàm số?
bởi Bùi Thị Hường
 06/07/2020
06/07/2020
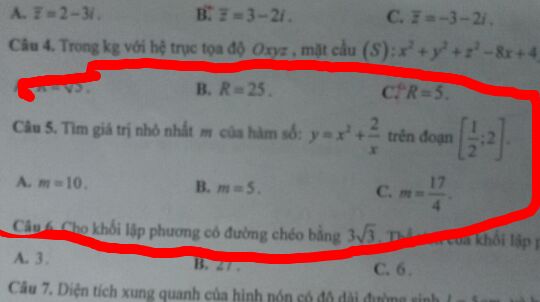 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính \(M^2+m^2\)?
bởi wibu
 03/07/2020
03/07/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là GTLN – GTNN của hàm số \(g\left( x \right) = f\left[ {2\left( {{{\sin }^4}x + {{\cos }^4}x} \right)} \right].\)
bởi Nguyễn Lệ Diễm
 30/05/2020
30/05/2020
.png)
Tổng M + m bằng
Theo dõi (0) 1 Trả lời -


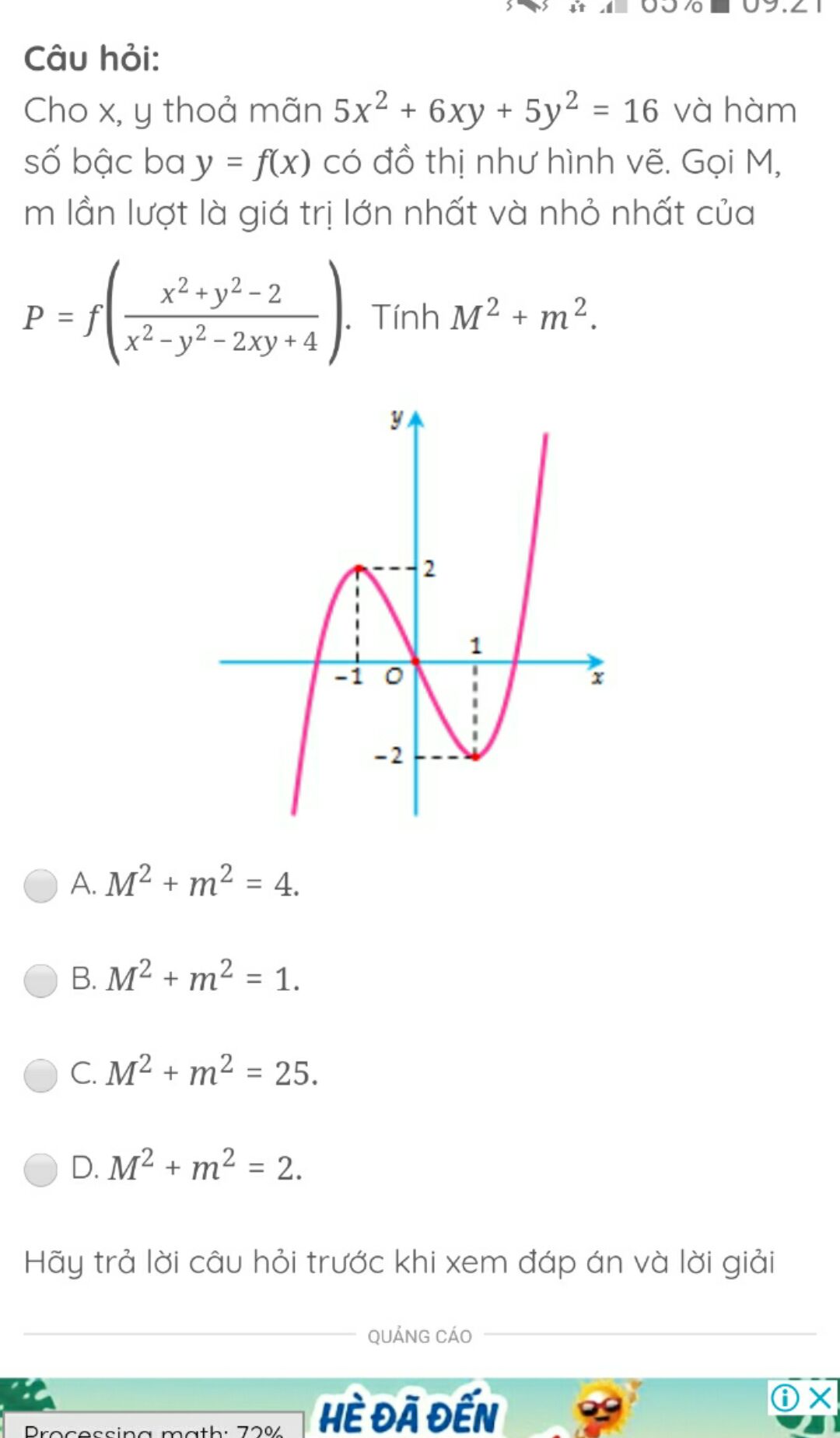
Cho x, y thoả mãn \(5{x^2} + 6xy + 5{y^2} = 16\) và hàm số bậc ba y = f(x) có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của \(P = f\left( {\frac{{{x^2} + {y^2} - 2}}{{{x^2} - {y^2} - 2xy + 4}}} \right).\) Tính \({M^2} + {m^2}.\)
bởi Trần Bảo Việt
 30/05/2020
30/05/2020
A. \({M^2} + {m^2}.=4\)
B. \({M^2} + {m^2}=1\)
C. \({M^2} + {m^2}=25\)
D. \({M^2} + {m^2}=2\)
Theo dõi (0) 1 Trả lời





.PNG)
