Giải bài 1.36 tr 21 SBT Toán 12
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x) = x + \frac{9}{x}\) trên đoạn [2;4].
Hướng dẫn giải chi tiết
TXĐ: \(D = R\backslash \left\{ 0 \right\}\)
\(\begin{array}{l}
f'\left( x \right) = 1 - \frac{9}{{{x^2}}} = \frac{{{x^2} - 9}}{{{x^2}}}\\
f'\left( x \right) = 0 \Leftrightarrow x = \pm 3
\end{array}\)
Hàm số nghịch biến trên các khoảng và đồng biến trên các khoảng
Bảng biến thiên:
.png)
Ta có \(\left[ {2;4} \right]\, \subset \left( {0; + \infty } \right);f\left( 2 \right) = 6,5;\)
\(f\left( 3 \right) = 6;f\left( 4 \right) = 6,25\)
Suy ra
\(\mathop {\max }\limits_{\left[ {2;4} \right]} f\left( x \right) = 6,5;\mathop {\min }\limits_{\left[ {2;4} \right]} f\left( x \right) = f\left( 3 \right) = 6\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1.34 trang 21 SBT Toán 12
Bài tập 1.35 trang 21 SBT Toán 12
Bài tập 1.37 trang 21 SBT Toán 12
Bài tập 1.38 trang 21 SBT Toán 12
Bài tập 1.39 trang 21 SBT Toán 12
Bài tập 1.40 trang 21 SBT Toán 12
Bài tập 1.41 trang 21 SBT Toán 12
Bài tập 1.42 trang 22 SBT Toán 12
Bài tập 1.43 trang 22 SBT Toán 12
Bài tập 1.44 trang 22 SBT Toán 12
Bài tập 1.45 trang 22 SBT Toán 12
Bài tập 1.46 trang 22 SBT Toán 12
Bài tập 16 trang 22 SGK Toán 12 NC
Bài tập 17 trang 22 SGK Toán 12 NC
Bài tập 18 trang 22 SGK Toán 12 NC
Bài tập 19 trang 22 SGK Toán 12 NC
Bài tập 20 trang 22 SGK Toán 12 NC
Bài tập 21 trang 22 SGK Toán 12 NC
Bài tập 22 trang 23 SGK Toán 12 NC
Bài tập 23 trang 23 SGK Toán 12 NC
Bài tập 24 trang 23 SGK Toán 12 NC
Bài tập 25 trang 23 SGK Toán 12 NC
Bài tập 26 trang 23 SGK Toán 12 NC
-
Cho x, y thoả mãn \(5{x^2} + 6xy + 5{y^2} = 16\) và hàm số bậc ba y = f(x) có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của \(P = f\left( {\frac{{{x^2} + {y^2} - 2}}{{{x^2} - {y^2} - 2xy + 4}}} \right).\) Tính \({M^2} + {m^2}.\)
bởi Trần Bảo Việt
30/05/2020
.PNG)
A. \({M^2} + {m^2}.=4\)
B. \({M^2} + {m^2}=1\)
C. \({M^2} + {m^2}=25\)
D. \({M^2} + {m^2}=2\)
Theo dõi (0) 1 Trả lời -
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Biết rằng \(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) và \(g\left( x \right) = f\left( {f\left( x \right)} \right)\). Tìm giá trị lớn nhất của hàm số g(x) trên đoạn [-3;-1].
bởi Trịnh Lan Trinh
31/05/2020
.png)
A. - 2 . B. 2 . C. 1 . D. \( - \frac{4}{3}\) .
Theo dõi (0) 1 Trả lời -
ADMICRO
Cho hàm số y = f(x) có đồ thị như hình vẽ. Khi đó hàm số \(y = f\left( {2 - {x^2}} \right)\) đạt GTLN trên \(\left[ {0;\sqrt 2 } \right]\) bằng
bởi Trần Bảo Việt
31/05/2020
.png)
A. f(0). B. f(1).
C. \(f\left( {\sqrt 2 } \right)\). D. f(2).
Theo dõi (0) 1 Trả lời -
Biết hàm số y = f(x) liên tục trên R có M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0;2]. Hàm số \(y = f\left( {\frac{{4x}}{{{x^2} + 1}}} \right)\) có tổng giá trị lớn nhất và nhỏ nhất là
bởi Nguyễn Lệ Diễm
30/05/2020
A. M + m. B.2M + m .
C. M + 2m. D. 2M + 2m.
Theo dõi (0) 1 Trả lời -
ADMICRO
Tìm giá trị nhỏ nhất của hàm số \(y = x + \dfrac{1}{x})trên ((0; +\infty)\)?
bởi Thời Tit
25/05/2020
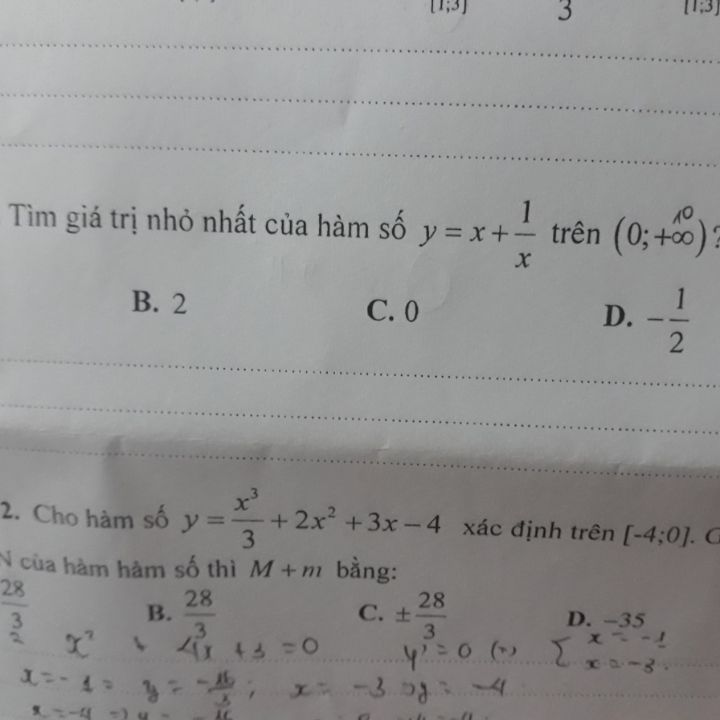Theo dõi (0) 1 Trả lời -
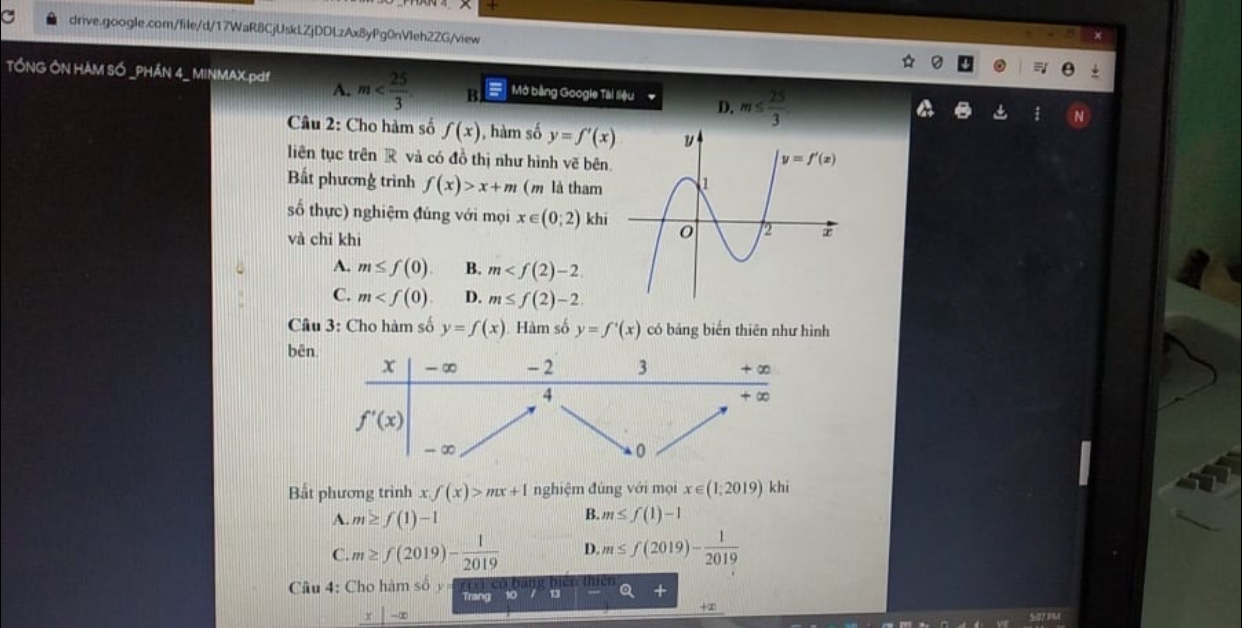
Tìm m để BPT đúng với mọi \(x \in (0;2)\)?
bởi Sơn Tới
06/05/2020
Câu 2 ạ
Theo dõi (0) 0 Trả lời -
Theo dõi (0) 7 Trả lời -
Tìm GTLN của hàm số cos^3x+2sinx+cosx
bởi Phạm Phương Thảo
17/04/2020
Tìm giá trị lớn nhất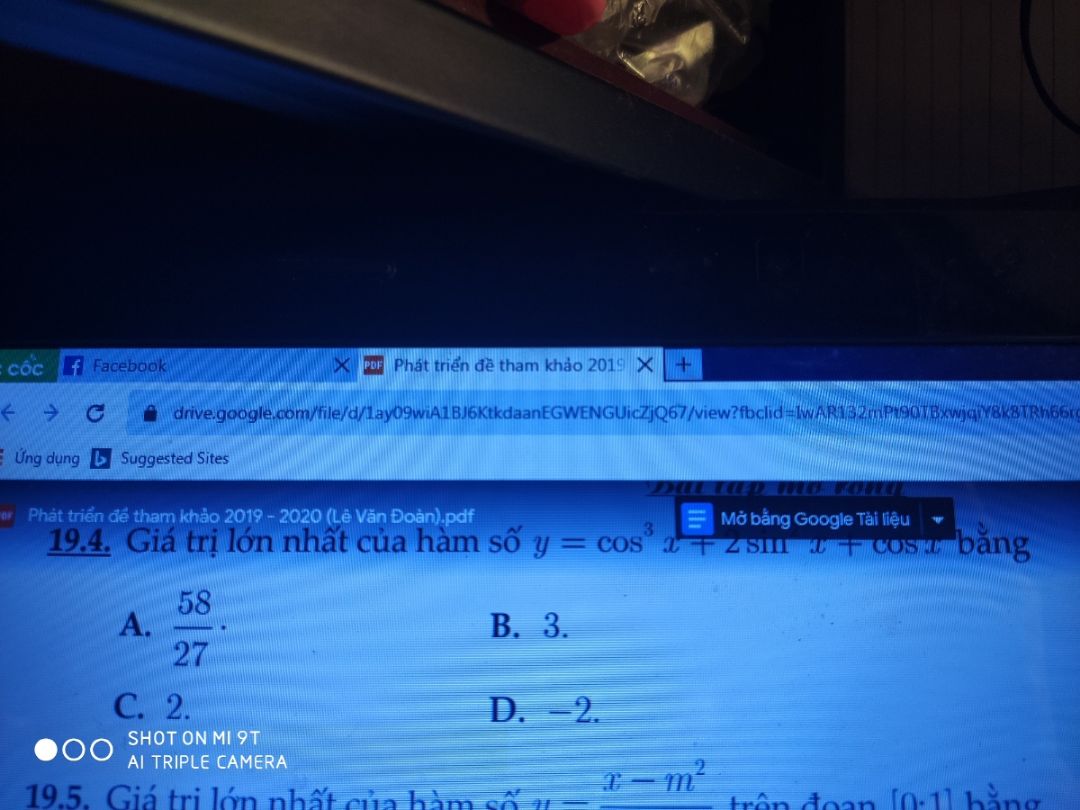
Theo dõi (1) 9 Trả lời -
Cho hàm số y=f(x) liên tục trên đoạn [-2;3] có đồ thị như hình bên khẳng định nào sai
bởi Đoàn Thị Phương
14/04/2020
Jjh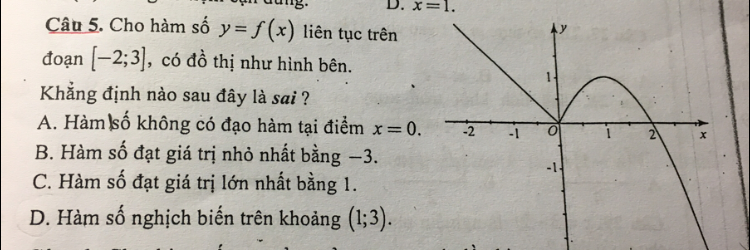
Theo dõi (0) 0 Trả lời -
Tìm GTLN, GTNN của hàm số f(x)
bởi lâm hữu thái
08/04/2020
Câu hỏi mức độ3,4 . Giải mình với các bạn
Theo dõi (0) 4 Trả lời -
Theo dõi (0) 3 Trả lời -
Tích của GTNN và GTLN của hs f(x)=x+4/x trên đoạn [1;3] bằng ?
Theo dõi (0) 2 Trả lời -
Gọi M, m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y= . Tính M - m.
bởi Trần Long
10/03/2020
gọi M, m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y=
. Tính M - m.
- M-m=3
- M-m=2
- M-m=4
- M-m=0
Theo dõi (0) 2 Trả lời -
Tìm giá trị nhỏ nhất của hàm số y=x-2/x-1 trên [2,4]
bởi tuong vi
25/02/2020
Tìm giá trị nhỏ nhất của hàm số y=x-2/x-1 trên [2,4]Theo dõi (0) 2 Trả lời -
Tìm giá trị nhỏ nhất GTLN của hàm số y = (5cos2x +1)/ 2
bởi Ana Đỗ
15/02/2020
Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y = 5 cos 2x 1 chia 2Theo dõi (0) 0 Trả lời -
Tìm gtln, gtnn của hàm số 1/3x+7
bởi Thu Thảo
29/12/2019
Tìm gtln gtnn của hàm số 1/3x 7Theo dõi (0) 0 Trả lời
