PhαΚßn hΤΑαΜ¦ng dαΚΪn giαΚΘi bΟ†i tαΚ≠p SGK bΟ†i Οîn tαΚ≠p chΤΑΤΓng III sαΚΫ giΟΚp cΟΓc em nαΚ·m ΡëΤΑαΜΘc phΤΑΤΓng phΟΓp vΟ† rΟ®n luyαΜ΅n kΡ© nΡÉng cΟΓc giαΚΘi bΟ†i tαΚ≠p vαΜ¹ VectΤΓ vΟ† quan hαΜ΅ vuΟ¥ng gΟ≥c trong khΟ¥ng gian tαΜΪ SGK HΟ§nh hαΜçc 11 CΤΓ bαΚΘn vΟ† NΟΔng cao.
-
BΟ†i tαΚ≠p 1 trang 120 SGK HΟ§nh hαΜçc 11
NhαΚ·c lαΚΓi ΡëαΜ΄nh nghΡ©a vectΤΓ khΟ¥ng gian. Cho hΟ§nh lΡÉng trαΜΞ tam giΟΓc ABC.A'B'C'. HΟΘy kαΜÉ tΟΣn nhαΜ·ng vectΤΓ bαΚ±ng \(\overrightarrow{AA'}\) cΟ≥ ΡëiαΜÉm ΡëαΚßu vΟ† ΡëiαΜÉm cuαΜëi lΟ† ΡëαΜânh cαΜßa hΟ§nh lΡÉng trαΜΞ.
-
BΟ†i tαΚ≠p 2 trang 120 SGK HΟ§nh hαΜçc 11
Trong khΟ¥ng gian cho ba vectΤΓ \(\vec{a}, \vec{b},\vec{c}\) ΡëαΜ¹u khΟΓc vectΤΓ khΟ¥ng . Khi nΟ†o ba vΟ©c tΤΓ ΡëΟ≥ ΡëαΜ™ng phαΚ≥ng?
-
BΟ†i tαΚ≠p 3 trang 120 SGK HΟ§nh hαΜçc 11
Trong khΟ¥ng gian, hai ΡëΤΑαΜùng thαΚ≥ng khΟ¥ng cαΚ·t nhau cΟ≥ thαΜÉ vuΟ¥ng gΟ≥c nhau khΟ¥ng? GiαΚΘ sαΜ≠ hai ΡëΤΑαΜùng thαΚ≥ng a, b lαΚßn lΤΑαΜΘt cΟ≥ vectΤΓ chαΜâ phΤΑΤΓng lΟ† \(\vec u\) vΟ† \(\vec v\). Khi nΟ†o ta cΟ≥ thαΜÉ kαΚΩt luαΚ≠n a vΟ† b vuΟ¥ng gΟ≥c nhau?
-
BΟ†i tαΚ≠p 4 trang 120 SGK HΟ§nh hαΜçc 11
MuαΜën chαΜ©ng minh ΡëΤΑαΜùng thαΚ≥ng a vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng \((\alpha )\) cΟ≥ cαΚßn chαΜ©ng minh a vuΟ¥ng gΟ≥c vαΜ¦i mαΜçi ΡëΤΑαΜùng thαΚ≥ng cαΜßa \((\alpha )\) hay khΟ¥ng?
- VIDEOYOMEDIA
-
BΟ†i tαΚ≠p 5 trang 120 SGK HΟ§nh hαΜçc 11
NhαΚ·c lαΚΓi nαΜôi dung ΡëαΜ΄nh lΟ≠ ba ΡëΤΑαΜùng thαΚ≥ng vuΟ¥ng gΟ≥c.
-
BΟ†i tαΚ≠p 6 trang 120 SGK HΟ§nh hαΜçc 11
NhαΚ·c lαΚΓi ΡëαΜ΄nh nghΡ©a:
a) GΟ≥c giαΜ·a ΡëΤΑαΜùng thαΚ≥ng vΟ† mαΚΖt phαΚ≥ng.
b) GΟ≥c giαΜ·a hai mαΚΖt phαΚ≥ng.
-
BΟ†i tαΚ≠p 7 trang 120 SGK HΟ§nh hαΜçc 11
MuαΜën chαΜ©ng minh mαΚΖt phαΚ≥ng \((\alpha )\) vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng \((\beta )\) thΟ§ phαΚΘi chαΜ©ng minh nhΤΑ thαΚΩ nΟ†o?
-
BΟ†i tαΚ≠p 8 trang 120 SGK HΟ§nh hαΜçc 11
HΟΘy nΟΣu cΟΓch tΟ≠nh khoαΚΘng cΟΓch:
a) TαΜΪ mαΜôt ΡëiαΜÉm ΡëαΚΩn mαΜôt ΡëΤΑαΜùng thαΚ≥ng;
b) TαΜΪ ΡëΤΑαΜùng thαΚ≥ng a ΡëαΚΩn mαΚΖt phαΚ≥ng \((\alpha )\) song song vαΜ¦i a;
c) GiαΜ·a hai mαΚΖt phαΚ≥ng song song.
-
BΟ†i tαΚ≠p 9 trang 120 SGK HΟ§nh hαΜçc 11
Cho a vΟ† b lΟ† hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau. CΟ≥ thαΜÉ tΟ≠nh khoαΚΘng cΟΓch giαΜ·a hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau nΟ†y bαΚ±ng nhαΜ·ng cΟΓch nΟ†o?
-
BΟ†i tαΚ≠p 10 trang 120 SGK HΟ§nh hαΜçc 11
ChαΜ©ng minh rαΚ±ng tαΚ≠p hαΜΘp cΟΓc ΡëiαΜÉm cΟΓch ΡëαΜ¹u ba ΡëαΜânh cαΜßa mαΜôt tam giΟΓc ABC lΟ† ΡëΤΑαΜùng vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (ABC) vΟ† Ρëi qua tΟΔm ΡëΤΑαΜùng trΟ≤n ngoαΚΓi tiαΚΩp tam giΟΓc ABC.
-
BΟ†i tαΚ≠p 1 trang 121 SGK HΟ§nh hαΜçc 11
Trong cΟΓc mαΜ΅nh ΡëαΜ¹ sau ΡëΟΔy, mαΜ΅nh ΡëαΜ¹ nΟ†o lΟ† ΡëΟΚng?
a) Hai ΡëΤΑαΜùng thαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng thΟ§ chΟΚng song song;
b) Hai mαΚΖt phαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ chΟΚng song song;
c) MαΚΖt phαΚ≥ng (\(\alpha\)) vuΟ¥ng gΟ≥c vαΜ¦i ΡëΤΑαΜùng thαΚ≥ng b vΟ† b vuΟ¥ng gΟ≥c vαΜ¦i thαΚ≥ng a, thΟ§ a song song vαΜ¦i (\(\alpha\)βÄ΄).
d) Hai mαΚΖt phαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng thΟ§ chΟΚng song song.
e) Hai ΡëΤΑαΜùng thαΚ≥ng cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ chΟΚng song song.
-
BΟ†i tαΚ≠p 2 trang 121 SGK HΟ§nh hαΜçc 11
CΟΓc ΡëiαΜ¹u khαΚ≥ng ΡëαΜ΄nh sau ΡëΟΔy, ΡëiαΜ¹u nΟ†o ΡëΟΚng?
a) KhoαΚΘng cΟΓch cαΜßa hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau lΟ† ΡëoαΚΓn ngαΚ·n nhαΚΞt trong cΟΓc ΡëoαΚΓn thαΚ≥ng nαΜëi hai ΡëiαΜÉm bαΚΞt kΟ§ nαΚ±m trΟΣn hai ΡëΤΑαΜùng thαΚ≥ng αΚΞy vΟ† ngΤΑαΜΘc lαΚΓi.
b) Qua mαΜôt ΡëiαΜÉm cΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng cho trΤΑαΜ¦c.
c) Qua mαΜôt ΡëΤΑαΜùng thαΚ≥ng cΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng khΟΓc cho trΤΑαΜ¦c.
d) ΡêΤΑαΜùng thαΚ≥ng nΟ†o vuΟ¥ng gΟ≥c vαΜ¦i cαΚΘ hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau cho trΤΑαΜ¦c lΟ† ΡëΤΑαΜùng vuΟ¥ng gΟ≥c chung cαΜßa hai ΡëΤΑαΜùng thαΚ≥ng ΡëΟ≥.
-
BΟ†i tαΚ≠p 3 trang 121 SGK HΟ§nh hαΜçc 11
HΟ§nh chΟ≥p S.ABCD cΟ≥ ΡëΟΓy ABCD lΟ† hΟ§nh vuΟ¥ng cαΚΓnh a, cαΚΓnh SA = a vΟ† vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (ABCD).
a) ChαΜ©ng minh rαΚ±ng cΟΓc mαΚΖt bΟΣn cαΜßa hΟ§nh chΟ≥p lΟ† nhαΜ·ng tam giΟΓc vuΟ¥ng.
b) MαΚΖt phαΚ≥ng (\(\alpha\)) Ρëi qua A vΟ† vuΟ¥ng gΟ≥c vαΜ¦i cαΚΓnh SC lαΚßn lΤΑαΜΘt cαΚ·t SB, AC, SD tαΚΓi B', C', D'. ChαΜ©ng minh B'D' song song vαΜ¦i BD vΟ† AB' vuΟ¥ng gΟ≥c vαΜ¦i SB.
-
BΟ†i tαΚ≠p 4 trang 121 SGK HΟ§nh hαΜçc 11
HΟ§nh chΟ≥p S.ABCD cΟ≥ ΡëΟΓy ABCD lΟ† hΟ§nh thoi cαΚΓnh a vΟ† cΟ≥ gΟ≥c \(\widehat{BAD} = 60^o\). GαΜçi O lΟ† giao ΡëiαΜÉm cαΜßa AC vΟ† BD. ΡêΤΑαΜùng thαΚ≥ng SO vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (ABCD) vΟ† \(SO = \frac{3a}{4}\). GαΜçi E lΟ† trung ΡëiαΜÉm cαΜßa ΡëoαΚΓn BC vΟ† F lΟ† trung ΡëiαΜÉm cαΜßa ΡëoαΚΓn BE.
a) ChαΜ©ng minh mαΚΖt phαΚ≥ng (SOF) vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (SBC).
b) TΟ≠nh cΟΓc khoαΚΘng cΟΓch tαΜΪ O vΟ† A ΡëαΚΩn mαΚΖt phαΚ≥ng (SBC).
-
BΟ†i tαΚ≠p 5 trang 121 SGK HΟ§nh hαΜçc 11
Cho tαΜ© diαΜ΅n ABCD cΟ≥ hai mαΚΖt ABC vΟ† ADC nαΚ±m trong hai mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i nhau. Tam giΟΓc ABC vuΟ¥ng tαΚΓi A cΟ≥ A vuΟ¥ng tαΚΓi D cΟ≥ CD = a.
a) ChαΜ©ng minh cΟΓc tam giΟΓc BAD vΟ† BDC lΟ† cΟΓc tam giΟΓc vuΟ¥ng.
b) GαΜçi I vΟ† K lαΚßn lΤΑαΜΘt lΟ† trung ΡëiαΜÉm cαΜßa Ad vΟ† BC. ChαΜ©ng minh IK lΟ† ΡëΤΑαΜùng vuΟ¥ng gΟ≥c chung cαΜßa hai ΡëΤΑαΜùng thαΚ≥ng AD vΟ† BC.
-
BΟ†i tαΚ≠p 6 trang 122 SGK HΟ§nh hαΜçc 11
Cho khαΜëi lαΚ≠p phΤΑΤΓng ABCD.A'B'C'D'cαΚΓnh a.
a) ChαΜ©ng minh BC' vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (A'B'CD).
b) XΟΓc ΡëαΜ΄nh vΟ† tΟ≠nh ΡëαΜô dΟ†i ΡëoαΚΓn vuΟ¥ng gΟ≥c chung cαΜßa AB' vΟ† BC'.
-
BΟ†i tαΚ≠p 7 trang 122 SGK HΟ§nh hαΜçc 11
Cho hΟ§nh chΟ≥p S.ABCD cΟ≥ ΡëΟΓy ABCD lΟ† hΟ§nh thoi cαΚΓnh a cΟ≥ gΟ≥c \(\widehat{BAD}=60^0\) vΟ† \(SA=SB=SD=\frac{a\sqrt{3}}{2}\).
a) TΟ≠nh khoαΚΘng cΟΓch tαΜΪ S ΡëαΚΩn mαΚΖt phαΚ≥ng (ABCD) vΟ† ΡëαΜô dΟ†i cαΚΓnh SC.
b) ChαΜ©ng minh mαΚΖt phαΚ≥ng (SAC) vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (ABCD).
c) ChαΜ©ng minh SB vuΟ¥ng gΟ≥c vαΜ¦i SC.
d) GαΜçi œÜ lΟ† gΟ≥c giαΜ·a hai mαΚΖt phαΚ≥ng (SBD) vΟ† (ABCD). TΟ≠nh tan œÜ.
-
BΟ†i tαΚ≠p 3.41 trang 161 SBT HΟ§nh hαΜçc 11
Trong cΟΓc khαΚ≥ng ΡëαΜ΄nh sau ΡëΟΔy khαΚ≥ng ΡëαΜ΄nh nΟ†o ΡëΟΚng? khαΚ≥ng ΡëαΜ΄nh nΟ†o sai?
a) Cho hai ΡëΤΑαΜùng thαΚ≥ng a vΟ† b song song vαΜ¦i nhau. NαΚΩu cΟ≥ mαΜôt ΡëΤΑαΜùng thαΚ≥ng d vuΟ¥ng gΟ≥c vαΜ¦i a thΟ§ d vuΟ¥ng gΟ≥c vαΜ¦i b.
b) Hai ΡëΤΑαΜùng thαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng thΟ§ chΟΚng song song vαΜ¦i nhau.
c) MαΜôt mαΚΖt phαΚ≥ng (Έ±) vΟ† mαΜôt ΡëΤΑαΜùng thαΚ≥ng a cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i ΡëΤΑαΜùng thαΚ±ng b thΟ§ a // (Έ±).
d) Hai mαΚΖt phαΚ≥ng (Έ±) vΟ† (Έ≤) phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng (Έ≥) thΟ§ (Έ±) // (Έ≤).
e) Hai ΡëΤΑαΜùng thαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ chΟΚng song song vαΜ¦i nhau.
f) Hai mαΚΖt phαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ chΟΚng song song.
-
BΟ†i tαΚ≠p 3.42 trang 161 SBT HΟ§nh hαΜçc 11
XΟ©t cΟΓc khαΚ≥ng ΡëαΜ΄nh sau ΡëΟΔy xem khαΚ≥ng ΡëαΜ΄nh nΟ†o ΡëΟΚng, khαΚ≥ng ΡëαΜ΄nh nΟ†o sai?
a) Qua mαΜôt ΡëiαΜÉm, cΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng cho trΤΑαΜ¦c.
b) Qua mαΜôt ΡëΤΑαΜùng thαΚ≥ng, cΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng cho trΤΑαΜ¦c.
c) Qua mαΜôt ΡëiαΜÉm, cΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng cho trΤΑαΜ¦c.
d) Cho hai ΡëΤΑαΜùng thαΚ≥ng a vΟ† b. NαΚΩu cΟ≥ mαΚΖt phαΚ≥ng (Έ±) khΟ¥ng chαΜ©a cαΚΘ a vΟ† b thΟ§ a vΟ† b chΟ©o nhau.
-
BΟ†i tαΚ≠p 3.43 trang 161 SBT HΟ§nh hαΜçc 11
TrΟΣn mαΚΖt phαΚ≥ng (Έ±) cho hΟ§nh vuΟ¥ng ABCD. CΟΓc tia Ax, By, Cz, Dt vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (Έ±) vΟ† nαΚ±m vαΜ¹ mαΜôt phΟ≠a ΡëαΜëi vαΜ¦i mαΚΖt phαΚ≥ng (Έ±). MαΜôt mαΚΖt phαΚ≥ng (Έ≤) lαΚßn lΤΑαΜΘt cαΚ·t Ax, By, Cz, Dt tαΚΓi A', B', C', D'.
a) TαΜ© giΟΓc A'B'C'D' lΟ† hΟ§nh gΟ§? ChαΜ©ng minh rαΚ±ng AAβÄ≤ + CCβÄ≤ = BBβÄ≤ + DDβÄ≤ = 2OOβÄ≤.
b) ChαΜ©ng minh rαΚ±ng ΡëiαΜ¹u kiαΜ΅n ΡëαΜÉ tαΜ© giΟΓc A'B'C'D' lΟ† hΟ§nh thoi lΟ† nΟ≥ cΟ≥ hai ΡëαΜânh ΡëαΜëi diαΜ΅n cΟΓch ΡëαΜ¹u mαΚΖt phαΚ≥ng (Έ±).
c) ChαΜ©ng minh rαΚ±ng ΡëiαΜ¹u kiαΜ΅n ΡëαΜÉ tαΜ© giΟΓc A'B'C'D' lΟ† hΟ§nh chαΜ· nhαΚ≠t lΟ† nΟ≥ cΟ≥ hai ΡëαΜânh kαΜ¹ nhau cΟΓch ΡëαΜ¹u mαΚΖt phαΚ≥ng (Έ±).
-
BΟ†i tαΚ≠p 3.44 trang 162 SBT HΟ§nh hαΜçc 11
HΟ§nh chΟ≥p tam giΟΓc S.ABC cΟ≥ ΡëΟΓy lΟ† tam giΟΓc ΡëαΜ¹u ABC cαΚΓnh 7a, cΟ≥ cαΚΓnh SC vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng ΡëΟΓy (ABC) vΟ† SC = 7a.
a) TΟ≠nh gΟ≥c giαΜ·a SA vΟ† BC.
b) TΟ≠nh khoαΚΘng cΟΓch giαΜ·a hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau SA vΟ† BC.
-
BΟ†i tαΚ≠p 3.45 trang 162 SBT HΟ§nh hαΜçc 11
Cho tαΜ© diαΜ΅n ABCD. ChαΜ©ng minh rαΚ±ng AB vuΟ¥ng gΟ≥c vαΜ¦i CD khi vΟ† chαΜâ khi AC2 + BD2 = AD2 + BC2
-
BΟ†i tαΚ≠p 3.46 trang 162 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh lαΚ≠p phΤΑΤΓng ABCD.A'B'C'D'. HΟΘy tΟ≠nh gΟ≥c cαΜßa cΟΓc cαΚΖp ΡëΤΑαΜùng thαΚ≥ng sau ΡëΟΔy:
a) AB' vφ BC'
b) AC' vφ CD'
-
BΟ†i tαΚ≠p 3.47 trang 162 SBT HΟ§nh hαΜçc 11
Cho hai tia Ax vΟ† By vuΟ¥ng gΟ≥c vαΜ¦i nhau nhαΚ≠n AB lΟ†m ΡëoαΚΓn vuΟ¥ng gΟ≥c chung. GαΜçi M vΟ† N lΟ† hai ΡëiαΜÉm di ΡëαΜông lαΚßn lΤΑαΜΘt trΟΣn Ax vΟ† By sao cho AM + BN = MN.
ΡêαΚΖt AB = 2a, gαΜçi O lΟ† trung ΡëiαΜÉm cαΜßa AB vΟ† H lΟ† hΟ§nh chiαΚΩu vuΟ¥ng gΟ≥c ΡëiαΜÉm O trΟΣn ΡëΤΑαΜùng thαΚ≥ng MN
a) ChαΜ©ng minh rαΚ±ng OH = a, HM = AN, HN = BN.
b) GαΜçi Bx' lΟ† tia song song vΟ† cΟΙng chiαΜ¹u vαΜ¦i tia Ax vΟ† K lΟ† hΟ§nh chiαΚΩu vuΟ¥ng gΟ≥c cαΜßa H trΟΣn mαΚΖt phαΚ≥ng (Bx'; By). ChαΜ©ng minh BK lΟ† phΟΔn giΟΓc cαΜßa gΟ≥c βà†x'By.
c) ChαΜ©ng minh ΡëiαΜÉm H nαΚ±m trΟΣn mαΜôt ΡëΤΑαΜùng trΟ≤n cαΜë ΡëαΜ΄nh.
-
BΟ†i tαΚ≠p 3.49 trang 163 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh chΟ≥p tαΜ© giΟΓc ΡëαΜ¹u S.ABCD. GαΜçi M, N lαΚßn lΤΑαΜΘt lΟ† trung ΡëiαΜÉm cαΜßa SA vΟ† SC.
a) ChαΜ©ng minh AC βäΞ SD
b) ChαΜ©ng minh MN βäΞ (SBD)
c) Cho AB = SA = a. TΟ≠nh cΟ¥sin cαΜßa gΟ≥c giαΜ·a (SBC) vΟ† (ABCD).
-
BΟ†i tαΚ≠p 3.50 trang 163 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh chΟ≥p S.ABC cΟ≥ ΡëΟΓy ABC lΟ† tam giΟΓc vuΟ¥ng tαΚΓi B, SA vuΟ¥ng gΟ≥c vαΜ¦i ΡëΟΓy.
a) ChαΜ©ng minh tam giΟΓc SBC vuΟ¥ng
b) GαΜçi H lΟ† chΟΔn ΡëΤΑαΜùng cao vαΚΫ tαΜΪ B cαΜßa tam giΟΓc ABC.
ChαΜ©ng minh (SAC) βäΞ (SBH)
c) Cho AB = a, BC = 2a. TΟ≠nh khoαΚΘng cΟΓch tαΜΪ B ΡëαΚΩn mαΚΖt phαΚ≥ng (SAC)
-
BΟ†i tαΚ≠p 3.51 trang 163 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh chΟ≥p S.ABCD, ΡëΟΓy ABCD lΟ† hΟ§nh thoi cαΚΓnh a, \(BAD = {60^0}\), SA = SB = SD = a.
a) ChαΜ©ng minh (SAC) vuΟ¥ng gΟ≥c vαΜ¦i (ABCD).
b) ChαΜ©ng minh tam giΟΓc SAC vuΟ¥ng.
c) TΟ≠nh khoαΚΘng cΟΓch tαΜΪ S ΡëαΚΩn (ABCD).
-
BΟ†i tαΚ≠p 3.52 trang 163 SBT HΟ§nh hαΜçc 11
Cho tαΜ© diαΜ΅n O.ABC cΟ≥ OA, OB, OC ΡëΟ¥i mαΜôt vuΟ¥ng gΟ≥c vΟ† cΟΓc cαΚΓnh OA = OB = OC = a, gαΜçi I lΟ† trung ΡëiαΜÉm BC.
a) ChαΜ©ng minh rαΚ±ng: BC βäΞ (AOI), (OAI) βäΞ (ABC).
b) TΟ≠nh gΟ≥c giαΜ·a AB vΟ† mαΚΖt phαΚ≥ng (AOI).
c) TΟ≠nh gΟ≥c giαΜ·a cΟΓc ΡëΤΑαΜùng thαΚ≥ng AI vΟ† OB.
-
BΟ†i tαΚ≠p 3.53 trang 163 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh chΟ≥p S.ABCD cΟ≥ ΡëΟΓy ABCD lΟ† hΟ§nh vuΟ¥ng cαΚΓnh bαΚ±ng a vΟ† SA βäΞ (ABCD).
a) ChαΜ©ng minh BD βäΞ SC.
b) ChαΜ©ng minh (SAB) βäΞ (SBC).
c) Cho \(SA = \frac{{a\sqrt 6 }}{3}\). TΟ≠nh gΟ≥c giαΜ·a SC vΟ† mαΚΖt phαΚ≥ng (ABCD).
-
BΟ†i tαΚ≠p 3.54 trang 164 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh hαΜôp ABCD.A'B'C'D' vαΜ¦i tΟΔm O. ΡêαΚ≥ng thαΜ©c nΟ†o sau ΡëΟΔy lΟ† Sai?
A. \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \)
B. \(\overrightarrow {AB} + \overrightarrow {BC'} + \overrightarrow {CD} + \overrightarrow {D'A} = \overrightarrow 0 \)
C. \(\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AD} + \overrightarrow {DD'} \)
D. \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC'} = \overrightarrow {AD'} + \overrightarrow {D'O} + \overrightarrow {OC'} \)
-
BΟ†i tαΚ≠p 3.55 trang 164 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh lΡÉng trαΜΞ tam giΟΓc ABC.A'B'C', ΡêαΚΖt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c ,\overrightarrow {BC} = \overrightarrow d \). ΡêαΚ≥ng thαΜ©c nΟ†o sau ΡëΟΔy ΡëΟΚng?
A. \(\overrightarrow a = \overrightarrow b + \overrightarrow c \)
B. \(\overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow d = \overrightarrow 0 \)
C. \(\overrightarrow b + \overrightarrow d - \overrightarrow c = \overrightarrow 0 \)
D. \(\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow d \)
-
BΟ†i tαΚ≠p 3.56 trang 164 SBT HΟ§nh hαΜçc 11
Cho tαΜ© diαΜ΅n ΡëαΜ¹u ABCD cΟ≥ cαΚΓnh bαΚ±ng a. KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy Sai?
A. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}\)
B. \(AB\bot CD\) hay \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow 0 \)
C. \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
D. \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \)
-
BΟ†i tαΚ≠p 3.57 trang 164 SBT HΟ§nh hαΜçc 11
KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. Cho hΟ§nh chΟ≥p S.ABCD. NαΚΩu cΟ≥ \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thΟ§ tαΜ© giΟΓc ABCD lΟ† hΟ§nh bΟ§nh hΟ†nh.
B. TαΜ© giΟΓc ABCD lΟ† hΟ§nh bΟ§nh hΟ†nh nαΚΩu \(\overrightarrow {AB} = \overrightarrow {CD} \).
C. TαΜ© giΟΓc ABCD lΟ† hΟ§nh bΟ§nh hΟ†nh nαΚΩu \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \)
D. TαΜ© giΟΓc ABCD lΟ† hΟ§nh bΟ§nh hΟ†nh nαΚΩu \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
-
BΟ†i tαΚ≠p 3.58 trang 164 SBT HΟ§nh hαΜçc 11
KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† Sai?
A. Ba vectΤΓ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) ΡëαΜ™ng phαΚ≥ng nαΚΩu cΟ≥ mαΜôt trong ba vectΤΓ ΡëΟ≥ bαΚ±ng vectΤΓ \(\overrightarrow 0\).
B. Ba vectΤΓ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) ΡëαΜ™ng phαΚ≥ng nαΚΩu cΟ≥ hai trong ba vectΤΓ ΡëΟ≥ cΟΙng phΤΑΤΓng.
C. Trong hΟ§nh hαΜôp ABCD.A'B'C'D' ba vectΤΓ \(\overrightarrow {AB'} ,\overrightarrow {C'A'} ,\overrightarrow {DA'} \) ΡëαΜ™ng phαΚ≥ng.
D. VectΤΓ \(\overrightarrow x = \overrightarrow a + \overrightarrow b + \overrightarrow c \) luΟ¥n ΡëαΜ™ng phαΚ≥ng vαΜ¦i hai vectΤΓ \(\overrightarrow a\) vΟ† \(\overrightarrow b\).
-
BΟ†i tαΚ≠p 3.59 trang 165 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh lαΚ≠p phΤΑΤΓng ABCD.A'B'C'D' cΟ≥ cαΚΓnh bαΚ±ng a. KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† Sai?
A. \(\overrightarrow {AC'} = a\sqrt 3 \)
B. \(\overrightarrow {AD'} .\overrightarrow {AB'} = {a^2}\)
C. \(\overrightarrow {AB'} .\overrightarrow {CD'} = 0\)
D. \(2\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {CD} + \overrightarrow {D'A'} = \overrightarrow 0 \)
-
BΟ†i tαΚ≠p 3.60 trang 165 SBT HΟ§nh hαΜçc 11
KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† Sai?
A. Cho hai vectΤΓ khΟ¥ng cΟΙng phΤΑΤΓng aβÜ£ vΟ† bβÜ£. Khi ΡëΟ≥ ba vectΤΓ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) ΡëαΜ™ng phαΚ≥ng khi vΟ† chαΜâ khi cΟ≥ cαΚΖp sαΜë m, n sao cho \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \), ngoΟ†i ra cαΚΖp sαΜë m, n lΟ† duy nhαΚΞt.
B. NαΚΩu cΟ≥ \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) vΟ† mαΜôt trong ba sαΜë m, n, p khΟΓc 0 thΟ§ ba vectΤΓ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) ΡëαΜ™ng phαΚ≥ng.
C. Ba vectΤΓ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) ΡëαΜ™ng phαΚ≥ng khi vΟ† chαΜâ khi ba vectΤΓ ΡëΟ≥ cΟΙng cΟ≥ giΟΓ trαΜ΄ thuαΜôc mαΜôt mαΚΖt phαΚ≥ng.
D. Ba tia Ox, Oy, Oz vuΟ¥ng gΟ≥c vαΜ¦i nhau tαΜΪng ΡëΟ¥i mαΜôt thΟ§ ba tia ΡëΟ≥ khΟ¥ng ΡëαΜ™ng phαΚ≥ng.
-
BΟ†i tαΚ≠p 3.61 trang 165 SBT HΟ§nh hαΜçc 11
Cho hai ΡëiαΜÉm phΟΔn biαΜ΅t A, B vΟ† mαΜôt ΡëiαΜÉm O bαΚΞt kΟ§. KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. ΡêiαΜÉm M thuαΜôc ΡëΤΑαΜùng thαΚ≥ng AB khi vΟ† chαΜâ khi \(\overrightarrow {OM} = \overrightarrow {OB} = k\overrightarrow {BA} \)
B. ΡêiαΜÉm M thuαΜôc ΡëΤΑαΜùng thαΚ≥ng AB khi vΟ† chαΜâ khi \(\overrightarrow {OM} = \overrightarrow {OB} = k\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right)\)
C. ΡêiαΜÉm M thuαΜôc ΡëΤΑαΜùng thαΚ≥ng AB khi vΟ† chαΜâ khi \(\overrightarrow {OM} = k\overrightarrow {OA} + \left( {1 - k} \right)\overrightarrow {OB} \)
D. ΡêiαΜÉm M thuαΜôc ΡëΤΑαΜùng thαΚ≥ng AB khi vΟ† chαΜâ khi \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \)
-
BΟ†i tαΚ≠p 3.62 trang 165 SBT HΟ§nh hαΜçc 11
KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. Hai ΡëΤΑαΜùng thαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng thΟ§ song song vαΜ¦i nhau.
B. Hai ΡëΤΑαΜùng thαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thαΜ© ba thΟ§ song song vαΜ¦i nhau.
C. Hai ΡëΤΑαΜùng thαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng thαΜ© ba thΟ§ song song vαΜ¦i nhau.
D. MαΚΖt phαΚ≥ng (Έ±) vΟ† ΡëΤΑαΜùng thαΚ≥ng a cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i ΡëΤΑαΜùng thαΚ≥ng b thΟ§ song song vαΜ¦i nhau.
-
BΟ†i tαΚ≠p 3.63 trang 165 SBT HΟ§nh hαΜçc 11
VαΜ¦i a, b, c lΟ† cΟΓc ΡëΤΑαΜùng thαΚ≥ng, khαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† Sai?
A. NαΚΩu a βäΞ b vΟ† b βäΞ c thΟ§ a // c;
B. NαΚΩu a// b vΟ† b βäΞ c thΟ§ a βäΞ c;
C. NαΚΩu a vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (Έ±) vΟ† b song song vαΜ¦i mαΚΖt phαΚ≥ng (Έ±) thΟ§ a βäΞ b;
D. NαΚΩu a βäΞ b, c βäΞ b vΟ† a cαΚ·t c thΟ§ b vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (a, c)
-
BΟ†i tαΚ≠p 3.64 trang 165 SBT HΟ§nh hαΜçc 11
Cho cΟΓc mαΜ΅nh ΡëαΜ¹ sau vαΜ¦i (Έ±) vΟ† (Έ≤) lΟ† hai mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i nhau vαΜ¦i giao tuyαΚΩn m = (Έ±) βà© (Έ≤) vΟ† a, b, c, d lΟ† cΟΓc ΡëΤΑαΜùng thαΚ≥ng. KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. NαΚΩu a βä² (Έ±) vΟ† a βäΞ m thΟ§ a βäΞ (Έ≤).
B. NαΚΩu b βäΞ m thΟ§ b βä² (Έ±) hoαΚΖc b βä² (Έ≤).
C. NαΚΩu c // m thΟ§ c // (Έ±) hoαΚΖc c // (Έ≤).
D. NαΚΩu d βäΞ m thΟ§ d βäΞ (Έ±)
-
BΟ†i tαΚ≠p 3.65 trang 165 SBT HΟ§nh hαΜçc 11
Cho a, b, c lΟ† cΟΓc ΡëΤΑαΜùng thαΚ≥ng. KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. NαΚΩu a βäΞ b vΟ† mαΚΖt phαΚ≥ng (Έ±) chαΜ©a a; mαΚΖt phαΚ≥ng (Έ≤) chαΜ©a b thΟ§ (Έ±) βäΞ (Έ≤)
B. Cho a βäΞ b vΟ† b nαΚ±m trong mαΚΖt phαΚ≥ng (Έ±). MαΜçi mαΚΖt phαΚ≥ng (Έ≤) chαΜ©a a vΟ† vuΟ¥ng gΟ≥c vαΜ¦i b thΟ§ (Έ≤) βäΞ (Έ±)
C. Cho a βäΞ b. MαΜçi mαΚΖt phαΚ≥ng chαΜ©a b ΡëαΜ¹u vuΟ¥ng gΟ≥c vαΜ¦i a.
D. Cho a // b. MαΜçi mαΚΖt phαΚ≥ng (Έ±) chαΜ©a c trong ΡëΟ≥ c βäΞ a vΟ† c βäΞ b thΟ§ ΡëαΜ¹u vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (a, b).
-
BΟ†i tαΚ≠p 3.66 trang 166 SBT HΟ§nh hαΜçc 11
KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. Qua mαΜôt ΡëΤΑαΜùng thαΚ≥ng, cΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng khΟΓc.
B. Qua mαΜôt ΡëiαΜÉm duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng cho trΤΑαΜ¦c.
C. Cho hai ΡëΤΑαΜùng thαΚ≥ng a vΟ† b vuΟ¥ng gΟ≥c vαΜ¦i nhau. NαΚΩu mαΚΖt phαΚ≥ng (Έ±) chαΜ©a a vΟ† mαΚΖt phαΚ≥ng (Έ≤) chαΜ©a b thΟ§ (Έ±) βäΞ (Έ≤).
D. Cho hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau a vΟ† b ΡëαΜ™ng thαΜùi a βäΞ b. LuΟ¥n cΟ≥ mαΚΖt phαΚ≥ng (Έ±) chαΜ©a a ΡëαΜÉ (Έ±) βäΞ b.
-
BΟ†i tαΚ≠p 3.67 trang 166 SBT HΟ§nh hαΜçc 11
KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. Cho hai ΡëΤΑαΜùng thαΚ≥ng a vΟ† b vuΟ¥ng gΟ≥c vαΜ¦i nhau, nαΚΩu mαΚΖt phαΚ≥ng (Έ±) chαΜ©a a vΟ† mαΚΖt phαΚ≥ng (Έ≤) chαΜ©a b thΟ§ (Έ±) βäΞ (Έ≤)
B. Cho ΡëΤΑαΜùng thαΚ≥ng a vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng (Έ±), mαΜçi mαΚΖt phαΚ≥ng (Έ≤) chαΜ©a a thΟ§ (Έ≤)βäΞ(Έ±)
C. Cho hai ΡëΤΑαΜùng thαΚ≥ng a vΟ† b vuΟ¥ng gΟ≥c vαΜ¦i nhau, mαΚΖt phαΚ≥ng nΟ†o vuΟ¥ng gΟ≥c vαΜ¦i ΡëΤΑαΜùng nΟ†y thΟ§ song song vαΜ¦i ΡëΤΑαΜùng kia.
D. Cho hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau a vΟ† b, luΟ¥n luΟ¥n cΟ≥ mαΜôt mαΚΖt phαΚ≥ng chαΜ©a ΡëΤΑαΜùng nΟ†y vΟ† vuΟ¥ng gΟ≥c vαΜ¦i ΡëΤΑαΜùng thαΚ≥ng kia.
-
BΟ†i tαΚ≠p 3.68 trang 166 SBT HΟ§nh hαΜçc 10
Cho tαΜ© diαΜ΅n ΡëαΜ¹u ABCD. KhoαΚΘng cΟΓch tαΜΪ ΡëiαΜÉm D tαΜ¦i mαΚΖt phαΚ≥ng (ABC) KHΟîNG BαΚΑNG ΡëαΜô dΟ†i ΡëoαΚΓn thαΚ≥ng nΟ†o dΤΑαΜ¦i ΡëΟΔy?
A. ΡêoαΚΓn nαΜëi tαΜΪ D ΡëαΚΩn trαΜçng tΟΔm cαΜßa tam giΟΓc ABC
B. ΡêoαΚΓn nαΜëi tαΜΪ D ΡëαΚΩn hΟ§nh chiαΚΩu vuΟ¥ng gΟ≥c cαΜßa ΡëiαΜÉm D trΟΣn mαΚΖt phαΚ≥ng (ABC)
C. ΡêoαΚΓn nαΜëi tαΜΪ D ΡëαΚΩn tΟΔm ΡëΤΑαΜùng trΟ≤n ngoαΚΓi tiαΚΩp tam giΟΓc ABC
D. ΡêoαΚΓn nαΜëi tαΜΪ D ΡëαΚΩn trung ΡëiαΜÉm cαΜßa ΡëoαΚΓn AM vαΜ¦i M lΟ† trung ΡëiαΜÉm cαΜßa ΡëoαΚΓn BC.
-
BΟ†i tαΚ≠p 3.69 trang 166 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh lαΚ≠p phΤΑΤΓng ABCD.A'B'C'D' cαΚΓnh a. KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. KhoαΚΘng cΟΓch tαΜΪ ΡëiαΜÉm A ΡëαΚΩn mαΚΖt phαΚ≥ng (A'BD) bαΚ±ng \(\frac{a}{3}\)
B. ΡêαΜô dΟ†i ΡëoαΚΓn AC' bαΚ±ng \(a\sqrt 3 \)
C. KhoαΚΘng cΟΓch tαΜΪ ΡëiαΜÉm A ΡëαΚΩn mαΚΖt phαΚ≥ng (CDD'C') bαΚ±ng \(a\sqrt 2 \)
D. KhoαΚΘng cΟΓch tαΜΪ ΡëiαΜÉm A ΡëαΚΩn mαΚΖt phαΚ≥ng (BCC'B') bαΚ±ng \(\frac{{3a}}{2}\).
-
BΟ†i tαΚ≠p 3.70 trang 167 SBT HΟ§nh hαΜçc 11
KhoαΚΘng cΟΓch giαΜ·a hai cαΚΓnh ΡëαΜëi trong mαΜôt tαΜ© diαΜ΅n ΡëαΜ¹u cαΚΓnh a lΟ†
A. \(\frac{{a\sqrt 2 }}{2}\) B. \(\frac{{a\sqrt 3 }}{3}\)
C. \(\frac{{2a}}{3}\) D. 2a
-
BΟ†i tαΚ≠p 3.71 trang 167 SBT HΟ§nh hαΜçc 11
HΟ§nh chΟ≥p tam giΟΓc ΡëαΜ¹u S.ABC cΟ≥ cαΚΓnh ΡëΟΓy bαΚ±ng 3a, cαΚΓnh bΟΣn bαΚ±ng 2a. KhoαΚΘng cΟΓch tαΜΪ ΡëαΜânh S tαΜ¦i mαΚΖt phαΚ≥ng ΡëΟΓy lΟ†
A. 1,5a B. a C. \({a\sqrt 2 }\) D. \({a\sqrt 3 }\)
-
BΟ†i tαΚ≠p 3.72 trang 167 SBT HΟ§nh hαΜçc 11
KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng?
A. ΡêΤΑαΜùng thαΚ≥ng vuΟ¥ng gΟ≥c chung cαΜßa hai ΡëΤΑαΜùng thαΚ≥ng a vΟ† b chΟ©o nhau lΟ† mαΜôt ΡëΤΑαΜùng thαΚ≥ng d vαΜΪa vuΟ¥ng gΟ≥c vαΜ¦i a vΟ† vαΜΪa vuΟ¥ng gΟ≥c vαΜ¦i b.
B. ΡêoαΚΓn vuΟ¥ng gΟ≥c chung cαΜßa hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau lΟ† ΡëoαΚΓn ngαΚ·n nhαΚΞt trong cΟΓc ΡëoαΚΓn nαΜëi hai ΡëiαΜÉm bαΚΞt kΟ§ lαΚßn lΤΑαΜΘt nαΚ±m trΟΣn hai ΡëΤΑαΜùng αΚΞy lΟ† ngΤΑαΜΘc lαΚΓi.
C. Cho hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau a vΟ† b. ΡêΤΑαΜùng vuΟ¥ng gΟ≥c chung luΟ¥n luΟ¥n nαΚ±m trong mαΚΖt phαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i a vΟ† chαΜ©a ΡëΤΑαΜùng thαΚ≥ng b.
D. Hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau lΟ† hai ΡëΤΑαΜùng thαΚ≥ng khΟ¥ng song song vαΜ¦i nhau.
-
BΟ†i tαΚ≠p 3.73 trang 168 SBT HΟ§nh hαΜçc 11
Cho hΟ§nh hαΜôp ABCD.A'B'C'D' cΟ≥ ba kΟ≠ch thΤΑαΜ¦c AB = a, AD = b, AA' = c. KhαΚ≥ng ΡëαΜ΄nh nΟ†o sau ΡëΟΔy lΟ† SAI?
A. ΡêαΜô dΟ†i ΡëΤΑαΜùng chΟ©o BD' bαΚ±ng \(\sqrt {{a^2} + {b^2} + {c^2}}\)
B. KhoαΚΘng cΟΓch giαΜ·a hai ΡëΤΑαΜùng thαΚ≥ng AB vΟ† CC' bαΚ±ng b.
C. KhoαΚΘng cΟΓch giαΜ·a hai ΡëΤΑαΜùng thαΚ≥ng BB' vΟ† DD' bαΚ±ng \(\sqrt {{a^2} + {b^2}} \)
D. KhoαΚΘng cΟΓch tαΜΪ A ΡëαΚΩn mαΚΖt phαΚ≥ng (A'BD) bαΚ±ng \(\frac{1}{3}\sqrt {{a^2} + {b^2} + {c^2}}\)
-
BΟ†i tαΚ≠p 1 trang 120 SGK HΟ§nh hαΜçc 11 NC
TαΜ© diαΜ΅n OABC cΟ≥ OA = OB = OC = a vΟ† \(\widehat {AOB} = \widehat {AOC} = {60^0},\widehat {BOC} = {90^0}\)
a. ChαΜ©ng tαΜè rαΚ±ng ABC lΟ† tam giΟΓc vuΟ¥ng vΟ† OA βäΞ BC
b. TΟ§m ΡëΤΑαΜùng vuΟ¥ng gΟ≥c chung IJ cαΜßa OA vΟ† BC ; tΟ≠nh khoαΚΘng cΟΓch giαΜ·a hai ΡëΤΑαΜùng thαΚ≥ng OA vΟ† BC.
c. ChαΜ©ng minh rαΚ±ng hai mαΚΖt phαΚ≥ng (ABC) vΟ† (OBC) vuΟ¥ng gΟ≥c vαΜ¦i nhau.
-
BΟ†i tαΚ≠p 2 trang 120 SGK HΟ§nh hαΜçc 11 NC
Cho hΟ§nh chΟ≥p S.ABC cΟ≥ SA = SB = SC = a, \(\widehat {ASB} = {120^ \circ },\widehat {BSC} = {60^ \circ },\widehat {CSA} = {90^ \circ }\)
a. ChαΜ©ng tαΜè rαΚ±ng ABC lΟ† tam giΟΓc vuΟ¥ng
b. TΟ≠nh khoαΚΘng cΟΓch tαΜΪ S ΡëαΚΩn mαΚΖt phαΚ≥ng (ABC)
-
BΟ†i tαΚ≠p 3 trang 120 SGK HΟ§nh hαΜçc 11 NC
Cho hΟ§nh chΟ≥p S.ABCD cΟ≥ ΡëΟΓy lΟ† hΟ§nh vuΟ¥ng cαΚΓnh a, SA βäΞ (ABCD). Hai ΡëiαΜÉm M vΟ† N lαΚßn lΤΑαΜΘt thay ΡëαΜïi trΟΣn cαΚΓnh CB vΟ† CD, ΡëαΚΖt CM = x, CN = y. TΟ§m hαΜ΅ thαΜ©c liΟΣn hαΜ΅ giαΜ·a x vΟ† y ΡëαΜÉ :
a. Hai mαΚΖt phαΚ≥ng (SAM) vΟ† (SAN) tαΚΓo vαΜ¦i nhau gΟ≥c 450
b. Hai mαΚΖt phαΚ≥ng (SAM) vΟ† (SMN) vuΟ¥ng gΟ≥c vαΜ¦i nhau.
-
BΟ†i tαΚ≠p 4 trang 120 SGK HΟ§nh hαΜçc 11 NC
Tam giΟΓc ABC vuΟ¥ng cΟ≥ cαΚΓnh huyαΜ¹n BC nαΚ±m trong mp(P), cαΚΓnh AB vΟ† AC lαΚßn lΤΑαΜΘt tαΚΓo vαΜ¦i mp(P) cΟΓc gΟ≥c Έ≤ vΟ† Έ≥. GαΜçi Έ± lΟ† gΟ≥c tαΚΓo bαΜüi mp(P) vΟ† mp(ABC).
ChαΜ©ng minh rαΚ±ng \(si{n^2}\alpha = si{n^2}\beta + si{n^2}\gamma \)
-
BΟ†i tαΚ≠p 5 trang 120 SGK HΟ§nh hαΜçc 11 NC
Cho tαΜ© diαΜ΅n OABC cΟ≥ OA, OB, OC ΡëΟ¥i mαΜôt vuΟ¥ng gΟ≥c vαΜ¦i nhau vΟ† OA = a, OB = b, OC = c. GαΜçi H lΟ† hΟ§nh chiαΚΩu cαΜßa O trΟΣn mαΚΖt phαΚ≥ng (ABC). TΟ≠nh diαΜ΅n tΟ≠ch cΟΓc tam giΟΓc HAB, HBC vΟ† HCA.
-
BΟ†i tαΚ≠p 6 trang 120 SGK HΟ§nh hαΜçc 11 NC
Cho hΟ§nh lΡÉng trαΜΞ ΡëαΜ©ng ABC.AβÄôBβÄôCβÄô cΟ≥ ΡëΟΓy ABC lΟ† tam giΟΓc vuΟ¥ng tαΚΓi ΡëαΜânh C, CA = a, CB = b ; mαΚΖt bΟΣn ABBβÄôAβÄô lΟ† hΟ§nh vuΟ¥ng. GαΜçi P lΟ† mαΚΖt phαΚ≥ng Ρëi qua C vΟ† vuΟ¥ng gΟ≥c vαΜ¦i ABβÄô.
a. XΟΓc ΡëαΜ΄nh thiαΚΩt diαΜ΅n cαΜßa hΟ§nh lΡÉng trαΜΞ ΡëΟΘ cho khi cαΚ·t bαΜüi (P). ThiαΚΩt diαΜ΅n lΟ† hΟ§nh gΟ§ ?
b. TΟ≠nh diαΜ΅n tΟ≠ch thiαΚΩt diαΜ΅n nΟ≥i trΟΣn.
-
BΟ†i tαΚ≠p 7 trang 121 SGK HΟ§nh hαΜçc 11 NC
MαΜôt tαΜ© diαΜ΅n ΡëΤΑαΜΘc gαΜçi lΟ† gαΚßn ΡëαΜ¹u nαΚΩu cΟΓc cαΚΓnh ΡëαΜëi bαΚ±ng nhau tαΜΪng ΡëΟ¥i mαΜôt. VαΜ¦i tαΜ© diαΜ΅n ABCD, chαΜ©ng tαΜè cΟΓc tΟ≠nh chαΚΞt sau lΟ† tΤΑΤΓng ΡëΤΑΤΓng :
a. TαΜ© diαΜ΅n ABCD lΟ† gαΚßn ΡëαΜ¹u ;
b. CΟΓc ΡëoαΚΓn thαΚ≥ng nαΜëi trung ΡëiαΜÉm cαΚΖp cαΚΓnh ΡëαΜëi diαΜ΅n ΡëΟ¥i mαΜôt vuΟ¥ng gΟ≥c vαΜ¦i nhau ;
c. CΟΓc trαΜçng tuyαΚΩn (ΡëoαΚΓn thαΚ≥ng nαΜëi ΡëαΜânh vαΜ¦i trαΜçng tΟΔm cαΜßa mαΚΖt ΡëαΜëi diαΜ΅n) bαΚ±ng nhau ;
d. TαΜïng cΟΓc gΟ≥c tαΚΓi mαΜ½i ΡëαΜânh bαΚ±ng 1800
-
BΟ†i tαΚ≠p 8 trang 121 SGK HΟ§nh hαΜçc 11 NC
Cho tαΜ© diαΜ΅n ABCD. CαΚ·t tαΜ© diαΜ΅n ΡëΟ≥ theo cΟΓc cαΚΓnh ΡëΟ≥ theo cΟΓc cαΚΓnh AB, AC, AD vΟ† trαΚΘi cΟΓc mαΚΖt ABC, ACD, ADB lΟΣn mαΚΖt phαΚ≥ng (BCD) (xem hΟ§nh 133). HΟ§nh phαΚ≥ng gαΜ™m cΟΓc tam giΟΓc BCD, A1BC, A2CD, A3BD gαΜçi lΟ† hΟ§nh khai triαΜÉn cαΜßa tαΜ© diαΜ΅n ABCD trΟΣn mαΚΖt phαΚ≥ng (BCD).
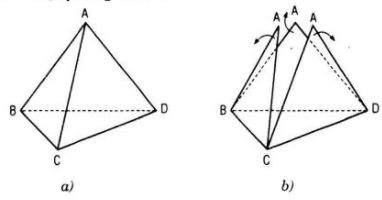
-
BΟ†i tαΚ≠p 1 trang 122 SGK HΟ§nh hαΜçc 11 NC
Cho tαΜ© diαΜ΅n ABCD cΟ≥ trαΜçng tΟΔm G. MαΜ΅nh ΡëαΜ¹ nΟ†o sau ΡëΟΔy lΟ† sai ?
A. \(\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\)
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\)
C. \(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\)
D. \(\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\)
-
BΟ†i tαΚ≠p 2 trang 122 SGK HΟ§nh hαΜçc 11 NC
MαΜ΅nh ΡëαΜ¹ nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng ?
A. Hai ΡëΤΑαΜùng thαΚ≥ng cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ song song vαΜ¦i nhau ;
B. Hai ΡëΤΑαΜùng thαΚ≥ng cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ vuΟ¥ng gΟ≥c vαΜ¦i nhau ;
C. MαΜôt ΡëΤΑαΜùng thαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt trong hai ΡëΤΑαΜùng thαΚ≥ng song song thΟ§ vuΟ¥ng gΟ≥c vαΜ¦i ΡëΤΑαΜùng thαΚ≥ng kia ;
D. MαΜôt ΡëΤΑαΜùng thαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt trong hai ΡëΤΑαΜùng thαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i nhau thΟ§ song song vαΜ¦i ΡëΤΑαΜùng thαΚ≥ng cΟ≤n lαΚΓi.
-
BΟ†i tαΚ≠p 3 trang 122 SGK HΟ§nh hαΜçc 11 NC
Cho hai ΡëΤΑαΜùng thαΚ≥ng phΟΔn biαΜ΅t a, b vΟ† mαΚΖt phαΚ≥ng (P), trong ΡëΟ≥ a βäΞ (P). MαΜ΅nh ΡëαΜ¹ nΟ†o sau ΡëΟΔy lΟ† sai ?
A. NαΚΩu b // (P) thΟ§ b βäΞ a
B. NαΚΩu b βäΞ (P) thΟ§ b // a
C. NαΚΩu b // a thΟ§ b βäΞ (P)
D. NαΚΩu b βäΞ a thΟ§ b // (P)
-
BΟ†i tαΚ≠p 4 trang 122 SGK HΟ§nh hαΜçc 11 NC
TΟ§m mαΜ΅nh ΡëαΜ¹ ΡëΟΚng trong cΟΓc mαΜ΅nh ΡëαΜ¹ sau :
A. Hai ΡëΤΑαΜùng thαΚ≥ng cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ song song ;
B. Hai ΡëΤΑαΜùng thαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ song song ;
C. Hai mαΚΖt phαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng thΟ§ song song ;
D. Hai mαΚΖt phαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng thΟ§ song song.
-
BΟ†i tαΚ≠p 5 trang 122 SGK HΟ§nh hαΜçc 11 NC
MαΜ΅nh ΡëαΜ¹ nΟ†o sau ΡëΟΔy lΟ† ΡëΟΚng ?
A. Hai ΡëΤΑαΜùng thαΚ≥ng vuΟ¥ng gΟ≥c vαΜ¦i nhau thΟ§ mαΜçi ΡëΤΑαΜùng thαΚ≥ng nαΚ±m trong mαΚΖt phαΚ≥ng nΟ†y sαΚΫ vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng kia ;
B. Hai mαΚΖt phαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng thΟ§ vuΟ¥ng gΟ≥c vαΜ¦i nhau ;
C. Hai mαΚΖt phαΚ≥ng phΟΔn biαΜ΅t cΟΙng vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng thΟ§ song song vαΜ¦i nhau ;
D. Ba mαΜ΅nh ΡëαΜ¹ trΟΣn ΡëαΜ¹u sai.
-
BΟ†i tαΚ≠p 6 trang 123 SGK HΟ§nh hαΜçc 11 NC
Trong cΟΓc mαΜ΅nh ΡëαΜ¹ sau, mαΜ΅nh ΡëαΜ¹ nΟ†o ΡëΟΚng ?
A. CΟ≥ duy nhαΚΞt mαΜôt ΡëΤΑαΜùng thαΚ≥ng Ρëi qua mαΜôt ΡëiαΜÉm cho trΤΑαΜ¦c vΟ† vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng cho trΤΑαΜ¦c ;
B. CΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng Ρëi qua mαΜôt ΡëΤΑαΜùng thαΚ≥ng cho trΤΑαΜ¦c vΟ† vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng cho trΤΑαΜ¦c ;
C. CΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng Ρëi qua mαΜôt ΡëiαΜÉm cho trΤΑαΜ¦c vΟ† vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt mαΚΖt phαΚ≥ng cho trΤΑαΜ¦c ;
D. CΟ≥ duy nhαΚΞt mαΜôt mαΚΖt phαΚ≥ng Ρëi qua mαΜôt ΡëiαΜÉm cho trΤΑαΜ¦c vΟ† vuΟ¥ng gΟ≥c vαΜ¦i mαΜôt ΡëΤΑαΜùng thαΚ≥ng cho trΤΑαΜ¦c.
-
BΟ†i tαΚ≠p 7 trang 123 SGK HΟ§nh hαΜçc 11 NC
TΟ§m mαΜ΅nh ΡëαΜ¹ ΡëΟΚng trong cΟΓc mαΜ΅nh ΡëαΜ¹ sau :
A. NαΚΩu hΟ§nh hαΜôp cΟ≥ hai mαΚΖt lΟ† hΟ§nh chαΜ· nhαΚ≠t thΟ§ nΟ≥ lΟ† hΟ§nh hαΜôp chαΜ· nhαΚ≠t ;
B. NαΚΩu hΟ§nh hαΜôp cΟ≥ ba mαΚΖt lΟ† hΟ§nh chαΜ· nhαΚ≠t thΟ§ nΟ≥ lΟ† hΟ§nh hαΜôp chαΜ· nhαΚ≠t ;
C. NαΚΩu hΟ§nh hαΜôp cΟ≥ bαΜën mαΚΖt lΟ† hΟ§nh chαΜ· nhαΚ≠t thΟ§ nΟ≥ lΟ† hΟ§nh hαΜôp chαΜ· nhαΚ≠t ;
D. NαΚΩu hΟ§nh hαΜôp cΟ≥ nΡÉm mαΚΖt lΟ† hΟ§nh chαΜ· nhαΚ≠t thΟ§ nΟ≥ lΟ† hΟ§nh hαΜôp chαΜ· nhαΚ≠t.
-
BΟ†i tαΚ≠p 8 trang 123 SGK HΟ§nh hαΜçc 11 NC
Trong cΟΓc mαΜ΅nh ΡëαΜ¹ sau, mαΜ΅nh ΡëαΜ¹ nΟ†o ΡëΟΚng ?
A. NαΚΩu hΟ§nh hαΜôp cΟ≥ hai mαΚΖt lΟ† hΟ§nh vuΟ¥ng thΟ§ nΟ≥ lΟ† hΟ§nh lαΚ≠p phΤΑΤΓng ;
B. NαΚΩu hΟ§nh hαΜôp cΟ≥ ba mαΚΖt chung mαΜôt ΡëαΜânh lΟ† hΟ§nh vuΟ¥ng thΟ§ nΟ≥ lΟ† hΟ§nh lαΚ≠p phΤΑΤΓng ;
C. NαΚΩu hΟ§nh hαΜôp cΟ≥ sΟΓu mαΚΖt bαΚ±ng nhau thΟ§ nΟ≥ lΟ† hΟ§nh lαΚ≠p phΤΑΤΓng ;
D. NαΚΩu hΟ§nh hαΜôp cΟ≥ bαΜën ΡëΤΑαΜùng chΟ©o bαΚ±ng nhau thΟ§ nΟ≥ lΟ† hΟ§nh lαΚ≠p phΤΑΤΓng.
-
BΟ†i tαΚ≠p 9 trang 123 SGK HΟ§nh hαΜçc 11 NC
Cho hΟ§nh chΟ≥p S.ABC cΟ≥ ΡëΟΓy lΟ† tam giΟΓc ΡëαΜ¹u. TΟ§m mαΜ΅nh ΡëαΜ¹ ΡëΟΚng trong cΟΓc mαΜ΅nh ΡëαΜ¹ sau :
A. S.ABC lΟ† hΟ§nh chΟ≥p ΡëαΜ¹u nαΚΩu cΟΓc mαΚΖt bΟΣn cαΜßa nΟ≥ lΟ† tam giΟΓc cΟΔn ;
B. S.ABC lΟ† hΟ§nh chΟ≥p ΡëαΜ¹u nαΚΩu cΟΓc mαΚΖt bΟΣn cαΜßa nΟ≥ lΟ† tam giΟΓc cΟΔn vαΜ¦i ΡëαΜânh S ;
C. S.ABC lΟ† hΟ§nh chΟ≥p ΡëαΜ¹u nαΚΩu gΟ≥c giαΜ·a cΟΓc mαΚΖt phαΚ≥ng chαΜ©a cΟΓc mαΚΖt bΟΣn vΟ† mαΚΖt phαΚ≥ng chαΜ©a ΡëΟΓy bαΚ±ng nhau ;
D. S.ABC lΟ† hΟ§nh chΟ≥p ΡëαΜ¹u nαΚΩu cΟΓc mαΚΖt bΟΣn cΟ≥ diαΜ΅n tΟ≠ch bαΚ±ng nhau.
-
BΟ†i tαΚ≠p 10 trang 123 SGK HΟ§nh hαΜçc 11 NC
TΟ§m mαΜ΅nh ΡëαΜ¹ ΡëΟΚng trong cΟΓc mαΜ΅nh ΡëαΜ¹ sau :
A. ΡêΤΑαΜùng vuΟ¥ng gΟ≥c chung cαΜßa hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau thΟ§ nαΚ±m trong mαΚΖt phαΚ≥ng chαΜ©a ΡëΤΑαΜùng thαΚ≥ng nΟ†y vΟ† vuΟ¥ng gΟ≥c vαΜ¦i ΡëΤΑαΜùng thαΚ≥ng kia ;
B. ΡêΤΑαΜùng vuΟ¥ng gΟ≥c chung cαΜßa hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau thΟ§ vuΟ¥ng gΟ≥c vαΜ¦i mαΚΖt phαΚ≥ng chαΜ©a ΡëΤΑαΜùng thαΚ≥ng nΟ†y vΟ† song song vαΜ¦i ΡëΤΑαΜùng thαΚ≥ng kia ;
C. MαΜôt ΡëΤΑαΜùng thαΚ≥ng lΟ† ΡëΤΑαΜùng vuΟ¥ng gΟ≥c chung cαΜßa hai ΡëΤΑαΜùng thαΚ≥ng chΟ©o nhau nαΚΩu nΟ≥ vuΟ¥ng gΟ≥c vαΜ¦i cαΚΘ hai ΡëΤΑαΜùng thαΚ≥ng ΡëΟ≥ ;
D. CΟΓc mαΜ΅nh ΡëαΜ¹ trΟΣn ΡëαΜ¹u sai.
-
BΟ†i tαΚ≠p 11 trang 124 SGK HΟ§nh hαΜçc 11 NC
HΟ§nh tαΜ© diαΜ΅n ABCD cΟ≥ AB, AC, AD ΡëΟ¥i mαΜôt vuΟ¥ng gΟ≥c lΟ† AB = AC = AD = 3.
DiαΜ΅n tΟ≠ch tam giΟΓc BCD bαΚ±ng
A. \(\frac{{9\sqrt 3 }}{2}\)
B. \(\frac{{9\sqrt 2 }}{3}\)
C. 27
D. \(\frac{{27}}{2}\)
-
BΟ†i tαΚ≠p 12 trang 124 SGK HΟ§nh hαΜçc 11 NC
HΟ§nh hαΜôp ABCD.AβÄôBβÄôCβÄôDβÄô cΟ≥ AB = AAβÄô = AD = a vΟ† \(\widehat {A'AB} = \widehat {A'AD} = \widehat {BAD} = {60^ \circ }\) Khi ΡëΟ≥, khoαΚΘng cΟΓch giαΜ·a cΟΓc ΡëΤΑαΜùng thαΚ≥ng chαΜ©a cΟΓc cαΚΓnh ΡëαΜëi diαΜ΅n cαΜßa tαΜ© diαΜ΅n AAβÄôBD bαΚ±ng :
A. \(\frac{{a\sqrt 2 }}{2}\)
B. \(\frac{{a\sqrt 3 }}{2}\)
C. \(a\sqrt 2 \)
D. \(\frac{{3a}}{2}\)


