Giải bài 1 tr 120 sách GK Toán Hình lớp 11
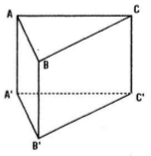
Nhắc lại định nghĩa vectơ không gian. Cho hình lăng trụ tam giác ABC.A'B'C'. Hãy kể tên những vectơ bằng \(\overrightarrow{AA'}\) có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
Gợi ý trả lời bài 1
Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
Vì các cạnh bên của hình lăng trụ là các đoạn thẳng song song và bằng nhau nên các vectơ bằng \(\overrightarrow{AA'}\) và có điểm đầu và điểm cuối là đỉnh của hình lăng trụ là: các vectơ \(\overrightarrow {BB'} ;\overrightarrow {CC'} ;\overrightarrow {DD'.}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 2 trang 120 SGK Hình học 11
Bài tập 3 trang 120 SGK Hình học 11
Bài tập 4 trang 120 SGK Hình học 11
Bài tập 5 trang 120 SGK Hình học 11
Bài tập 6 trang 120 SGK Hình học 11
Bài tập 7 trang 120 SGK Hình học 11
Bài tập 8 trang 120 SGK Hình học 11
Bài tập 9 trang 120 SGK Hình học 11
Bài tập 10 trang 120 SGK Hình học 11
Bài tập 1 trang 121 SGK Hình học 11
Bài tập 2 trang 121 SGK Hình học 11
Bài tập 3 trang 121 SGK Hình học 11
Bài tập 4 trang 121 SGK Hình học 11
Bài tập 5 trang 121 SGK Hình học 11
Bài tập 6 trang 122 SGK Hình học 11
Bài tập 7 trang 122 SGK Hình học 11
Bài tập 3.41 trang 161 SBT Hình học 11
Bài tập 3.42 trang 161 SBT Hình học 11
Bài tập 3.43 trang 161 SBT Hình học 11
Bài tập 3.44 trang 162 SBT Hình học 11
Bài tập 3.45 trang 162 SBT Hình học 11
Bài tập 3.46 trang 162 SBT Hình học 11
Bài tập 3.47 trang 162 SBT Hình học 11
Bài tập 3.49 trang 163 SBT Hình học 11
Bài tập 3.50 trang 163 SBT Hình học 11
Bài tập 3.51 trang 163 SBT Hình học 11
Bài tập 3.52 trang 163 SBT Hình học 11
Bài tập 3.53 trang 163 SBT Hình học 11
Bài tập 3.54 trang 164 SBT Hình học 11
Bài tập 3.55 trang 164 SBT Hình học 11
Bài tập 3.56 trang 164 SBT Hình học 11
Bài tập 3.57 trang 164 SBT Hình học 11
Bài tập 3.58 trang 164 SBT Hình học 11
Bài tập 3.59 trang 165 SBT Hình học 11
Bài tập 3.60 trang 165 SBT Hình học 11
Bài tập 3.61 trang 165 SBT Hình học 11
Bài tập 3.62 trang 165 SBT Hình học 11
Bài tập 3.63 trang 165 SBT Hình học 11
Bài tập 3.64 trang 165 SBT Hình học 11
Bài tập 3.65 trang 165 SBT Hình học 11
Bài tập 3.66 trang 166 SBT Hình học 11
Bài tập 3.67 trang 166 SBT Hình học 11
Bài tập 3.68 trang 166 SBT Hình học 10
Bài tập 3.69 trang 166 SBT Hình học 11
Bài tập 3.70 trang 167 SBT Hình học 11
Bài tập 3.71 trang 167 SBT Hình học 11
Bài tập 3.72 trang 167 SBT Hình học 11
Bài tập 3.73 trang 168 SBT Hình học 11
Bài tập 1 trang 120 SGK Hình học 11 NC
Bài tập 2 trang 120 SGK Hình học 11 NC
Bài tập 3 trang 120 SGK Hình học 11 NC
Bài tập 4 trang 120 SGK Hình học 11 NC
Bài tập 5 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC
-


Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA vuông góc với đáy và SA = a√3. Gọi AE, AH lần lượt là các đường cao của ΔSAB và ΔSAD
bởi Quân Đỗ
 22/04/2023
22/04/2023
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA vuông góc với đáy và SA = a√3a3. Gọi AE, AH lần lượt là các đường cao của ΔSAB và ΔSAD
1) Chứng minh rằng: BC ⊥ (SAB), BD ⊥ (SAC)
2) Chứng minh rằng: (SAD) ⊥ (SDC)
3) Chứng minh rằng: AE ⊥ SC và AH ⊥ SC
4) Tính góc giữa: đường thẳng SC và mặt phẳng (SAB), đường thẳng SB và mặt phẳng (SAC)
5) Tính góc giữa (SBD) và (ABCD)
6) Tính khoảng cách từ điểm O đến mặt phẳng (SCD)
Theo dõi (0) 0 Trả lời -


Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC= a, AD=2a; Cạnh bên SA vuông góc với mặt đáy và SA=a. Chứng minh BC vuông góc với mặt phẳng (SAB). Từ đó suy ra tam giác SBC vuông tại B.
bởi Lam Van
 17/03/2023
17/03/2023
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B,
AB=BC= a, AD=2a; Cạnh bên SA vuông góc với mặt đáy và SA=a.
a) Chứng minh BC vuông góc với mặt phẳng (SAB). Từ đó suy ra tam giác SBC vuông tại B.
b) Xác định và tính góc giữa SC và mặt phẳng (SAD).
Theo dõi (0) 1 Trả lời -


Cho hình chóp tam giác đều, cạnh đáy bằng a, cạnh bên bằng 2a.Tính góc giữa các cạnh bên
bởi Tên
 25/04/2022
Nhanh giúp mk vsTheo dõi (1) 0 Trả lời
25/04/2022
Nhanh giúp mk vsTheo dõi (1) 0 Trả lời -


Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc, SA=a, SB=2a, SC=3a. H là hình chiếu của S trên mặt phẳng (ABC). Tính: 1. (SB,(SAC)) 2. (AH,(SBC))
bởi Linh
 13/05/2021
Cho hình chóp S.ABC có SA SB SC đôi một vuông góc SA=a SB=2a SC=3a H là hình chiếu của S trên măt phăng (ABC) Tính: 1.(sb;(sac)) 2.(AH;(SBC)) (AH,(ABC)) 3.((sbc));(abc)) ((sac);(sbc))Theo dõi (0) 0 Trả lời
13/05/2021
Cho hình chóp S.ABC có SA SB SC đôi một vuông góc SA=a SB=2a SC=3a H là hình chiếu của S trên măt phăng (ABC) Tính: 1.(sb;(sac)) 2.(AH;(SBC)) (AH,(ABC)) 3.((sbc));(abc)) ((sac);(sbc))Theo dõi (0) 0 Trả lời


