Bài tập 6 trang 120 SGK Hình học 11 NC

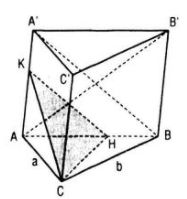
a) Kẻ đường cao CH của tam giác vuông ABC thì CH ⊥ AB’ (định lí ba đường vuông góc).

Trong mp(ABB’A’) kẻ đường thẳng Ht vuông góc với AB’.

Khi đó (P) chính là mp(CHt).

Chú ý rằng do ABB’A’ là hình vuông nên AB’ ⊥ A’B. Vậy Ht // A’B, từ đó Ht cắt AA’ tại điểm K thuộc đoạn AA’.

Như vậy, thiết diện của hình lăng trụ ABC.A’B’C’ khi cắt bởi mp(P) là tam giác CHK.

Do CH ⊥ AB, mp(ABB’A’) ⊥ mp(ABC) nên CH ⊥ (ABB’A’), từ đó tam giác CHK vuông tại H.

b)

\(\begin{array}{*{20}{l}}
{{S_{CHK}} = \frac{1}{2}CH.HK}\\
\begin{array}{l}
CH.AB = CA.CB\\
 \Rightarrow CH = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}
\end{array}\\
{AH.AB = {a^2} \Rightarrow AH = \frac{{{a^2}}}{{AB}}}\\
{\frac{{HK}}{{A\prime B}} = \frac{{AH}}{{AB}}}\\
{ \Rightarrow HK = A\prime B.\frac{{{a^2}}}{{A{B^2}}}}\\
{ = \frac{{\sqrt {{a^2} + {b^2}} .\sqrt 2 {a^2}}}{{{a^2} + {b^2}}} = \frac{{{a^2}\sqrt 2 }}{{\sqrt {{a^2} + {b^2}} }}}
\end{array}\)

Từ đó: 

\(\begin{array}{l}
{S_{CHK}} = \frac{1}{2}\frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}.\frac{{{a^2}\sqrt 2 }}{{\sqrt {{a^2} + {b^2}} }}\\
 = \frac{{{a^3}b\sqrt 2 }}{{2\left( {{a^2} + {b^2}} \right)}}
\end{array}\)

-- Mod Toán 11 HỌC247