Bài tập 5 trang 120 SGK Hình học 11 NC
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
Hướng dẫn giải chi tiết
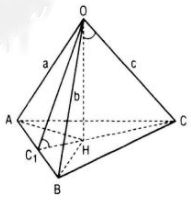
Vì OA, OB, OC đôi một vuông góc và H là hình chiếu của O trên mp(ABC) nên H là trực tâm tam giác ABC.
Từ đó HC1 ⊥ AB (C1 là giao điểm của CH và AB), suy ra OC1 ⊥ AB.
Như vậy \(\widehat {O{C_1}H}\) là góc giữa mp(OAB) và mp(ABC).
Ta có: \({S_{HAB}} = {S_{OAB}}cos\widehat {O{C_1}H}\)
Mà \(\widehat {O{C_1}H} = \widehat {HOC}\)
Nên \({S_{HAB}} = {S_{OAB}}cos\widehat {HOC}\)
Ta lại có:
\(\begin{array}{l}
\cos \widehat {HOC} = \frac{{OH}}{{OC}},\\
\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}
\end{array}\)
Từ đó:
\(cos\widehat {HOC} = \frac{{ab}}{{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Mặt khác \({S_{OAB}} = \frac{1}{2}ab\)
Vậy \({S_{HAB}} = \frac{{{a^2}{b^2}}}{{2\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Tương tự như trên, ta có
\({S_{HBC}} = \frac{{{b^2}{c^2}}}{{2\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
\({S_{HAC}} = \frac{{{b^2}{c^2}}}{{2\sqrt {{c^2}{a^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3 trang 120 SGK Hình học 11 NC
Bài tập 4 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC
-


Cm A,C',M,N thẳng hàng, biết M, N là trọng tâm của tam giác BDA', B'D'C'
bởi Phạm Khánh Ngọc
 25/10/2018
25/10/2018
Cho hình hộp ABCD.A'B'C'D'. Gọi M. N theo thứ tự là trọng tâm của cá tam giác BDA', B'D'C'. Chứng minh rằng A,C',M,N thẳng hàng.
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD. Gọi M và N theo thứ tự là trung điểm của các cạnh AB và CD. Lấy P thuộc CM và Q thuộc AN sao cho AQ : QN = CP:PM=2:1. Chứng minh rằng B,D,P và Q thẳng hàng.
Theo dõi (0) 1 Trả lời -


Cm E,F,M,N cùng nằm trên 1 đường thẳng biết M, N là trung điểm AB, CD
bởi Nguyễn Thanh Hà
 01/11/2018
01/11/2018
Cho tứ giác ABCD có AB song song với CD. Các đường thẳng AC, BD cắt nhau ở E và các đường thẳng AD, BC cắt nhau ở F. Gọi M, N theo thứ tự là trung điểm cạnh AB, CD. Chứng minh rằng E, F, M, N cùng nằm trên một đường thẳng.
Theo dõi (0) 1 Trả lời -


Cm MN là đoạn vuông góc chung của CA và BD
bởi can chu
 01/11/2018
01/11/2018
Cho tứ diện ABCD có AB=CD, BC=DA. Gọi M, N theo thứ tự là trung điểm của CA, BD.
Chứng minh rằng MN là đoạn vuông góc chung của các đường thẳng CA và BD
Theo dõi (0) 1 Trả lời





