Bài tập 3 trang 120 SGK Hình học 11 NC
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM = x, CN = y. Tìm hệ thức liên hệ giữa x và y để :
a. Hai mặt phẳng (SAM) và (SAN) tạo với nhau góc 450
b. Hai mặt phẳng (SAM) và (SMN) vuông góc với nhau.
Hướng dẫn giải chi tiết
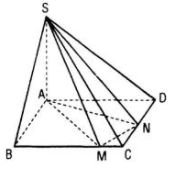
a) Ta có: AM, AN cùng vuông góc với SA mà \(\widehat {MAN} \le {90^0}\) nên \(\widehat {MAN}\) là góc giữa hai mặt phẳng (SAM) và (SAN). Hai mặt phẳng đó tạo với nhau góc 45˚ khi và chỉ khi \(\widehat {MAN} = {45^0}\)
Mặt khác, \(M \in BC,N \in CD,\widehat {BAD} = {90^ \circ }\) n
nên điều đó xảy ra khi \(\widehat {BAM} + \widehat {DAN} = {45^0}\)
Từ đó ta có:
\(1 = \frac{{\tan \widehat {BAM} + \tan \widehat {DAN}}}{{1 - \tan \widehat {BAM}.\tan \widehat {DAN}}}\left( * \right)\)
(\(\tan \left( {x + y} \right) = \frac{{\tan x + \tan y}}{{1 - \tan x\tan y}}\))
Vì \(tan\widehat {BAM} = \frac{{a - x}}{a},tan\widehat {DAN} = \frac{{a - y}}{a}\)
Nên (∗) \( \Leftrightarrow 2{a^2} + xy = 2a(x + y)\)
\( \Leftrightarrow 2a^2+xy = 2a(x+y)\)
Đó là hệ thức liên hệ giữa x và y để các mặt phẳng (SAM) và (SAN) tạo với nhau góc 450
B) Ta có: (SAM) ⊥ (ABCD), từ đó nếu (SMN) ⊥ (SAM) thì giao tuyến MN của (SMN) và (ABCD) sẽ vuông góc với (SAM), tức MN ⊥ AM.
Ngược lại, nếu có MN ⊥ AM thì do SA ⊥ MN nên MN ⊥ (SAM), suy ra (SMN) ⊥ (SAM).
Vậy (SAM) ⊥ (SMN) khi và chỉ khi \(\widehat {AMN} = {90^0}\)
\( \Leftrightarrow {a^2} + {(a - x)^2} + {x^2} + {y^2} = {a^2} + {(a - y)^2}\)
\( \Leftrightarrow ay = x(a - x)0\) với \(0 \le x \le a,0 \le y \le a\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 1 trang 120 SGK Hình học 11 NC
Bài tập 2 trang 120 SGK Hình học 11 NC
Bài tập 4 trang 120 SGK Hình học 11 NC
Bài tập 5 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC
-


Chứng minh AB^2+BC^2+CD^2+DA^2=AC^2+BD^2+4IJ^2
bởi Mai Anh
 01/11/2018
01/11/2018
Cho tứ giác ABCD. Gọi I. J theo thứ tự là trung điểm AC, BD
1. Chứng minh rằng \(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2+4ỊJ^2\)
2. Chứng minh rằng \(AB^2+BC^2+CD^2+DA^2\ge AC^2+BD^2\)
Theo dõi (0) 1 Trả lời -


Tìm tập hợp tất cả các điểm M để MA/MB=k biết k là số thực dương khác 0
bởi Trần Phương Khanh
 01/11/2018
01/11/2018
Trong mặt phẳng cho trước hai điểm A, B và k là một số thực dương khác 1 cho trước. Tìm tập hợp tất cả các điểm M (của mặt phẳng) sao cho \(\frac{MA}{MB}=k\)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC. Xét các điểm M thuộc BC, N thuộc CA và P thuộc AB sao cho tứ giác APMN là một hình bình hành. Gọi O là giao điểm của các đường thẳng BN và CP. Xác định vị trí hình học của điểm M trên cạnh BC sao cho góc PMO= góc OMP
Theo dõi (0) 1 Trả lời -


Cho hình lăng trụ ABC.A'B'C'. Gọi M. N theo thứ tự là trung điểm các cạnh BB', C'A' và P là điểm trên cạnh B'C' sao cho C'P = 2PB'.
Chứng minh rằng A, M, N và P đồng phẳng.
Theo dõi (0) 1 Trả lời



