Giải bài 3.44 tr 162 SBT Hình học 11
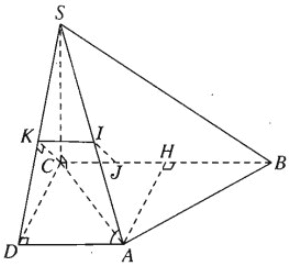
Hình chóp tam giác S.ABC có đáy là tam giác đều ABC cạnh 7a, có cạnh SC vuông góc với mặt phẳng đáy (ABC) và SC = 7a.
a) Tính góc giữa SA và BC.
b) Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
Hướng dẫn giải chi tiết
a) Gọi H là trung điểm của đoạn BC. Qua A vẽ AD song song với BC và bằng HC thì góc giữa BC và SA là góc \(\widehat {SAD}\).
Theo định lí ba đường vuông góc, ta có SD ⊥ DA và khi đó:
\(\cos \widehat {SAD} = \frac{{AD}}{{SA}} = \frac{{HC}}{{SA}} = \frac{{\frac{{7a}}{2}}}{{7a\sqrt 2 }} = \frac{{\sqrt 2 }}{4}\)
Vậy góc giữa BC và SA được xác định sao cho \(\cos \widehat {SAD} = \frac{{\sqrt 2 }}{4}\).
b) Vì BC // AD nên BC // mp(SAD). Do đó \(d\left( {SA,BC} \right) = d\left( {BC,\left( {SAD} \right)} \right)\).
Kẻ CK ⊥ SD ⇒ CK ⊥ (SAD), do đó CK chính là khoảng cách nói trên.
Xét tam giác vuông SCD với đường cao CK xuất phát từ đỉnh góc vuông C ta có hệ thức:
\(\frac{1}{{C{K^2}}} = \frac{1}{{S{C^2}}} + \frac{1}{{C{D^2}}} = \frac{1}{{{{\left( {7a} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{7a\sqrt 3 }}{2}} \right)}^2}}}\)
(vì \(CD = AH = \frac{{BC\sqrt 3 }}{2} = \frac{{7a\sqrt 3 }}{2}\))
Do đó \(\frac{1}{{C{K^2}}} = \frac{1}{{21{a^2}}} \Rightarrow C{K^2} = a\sqrt {21} \)
Vậy \(d\left( {SA,BC} \right) = a\sqrt {21} \).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3.42 trang 161 SBT Hình học 11
Bài tập 3.43 trang 161 SBT Hình học 11
Bài tập 3.45 trang 162 SBT Hình học 11
Bài tập 3.46 trang 162 SBT Hình học 11
Bài tập 3.47 trang 162 SBT Hình học 11
Bài tập 3.49 trang 163 SBT Hình học 11
Bài tập 3.50 trang 163 SBT Hình học 11
Bài tập 3.51 trang 163 SBT Hình học 11
Bài tập 3.52 trang 163 SBT Hình học 11
Bài tập 3.53 trang 163 SBT Hình học 11
Bài tập 3.54 trang 164 SBT Hình học 11
Bài tập 3.55 trang 164 SBT Hình học 11
Bài tập 3.56 trang 164 SBT Hình học 11
Bài tập 3.57 trang 164 SBT Hình học 11
Bài tập 3.58 trang 164 SBT Hình học 11
Bài tập 3.59 trang 165 SBT Hình học 11
Bài tập 3.60 trang 165 SBT Hình học 11
Bài tập 3.61 trang 165 SBT Hình học 11
Bài tập 3.62 trang 165 SBT Hình học 11
Bài tập 3.63 trang 165 SBT Hình học 11
Bài tập 3.64 trang 165 SBT Hình học 11
Bài tập 3.65 trang 165 SBT Hình học 11
Bài tập 3.66 trang 166 SBT Hình học 11
Bài tập 3.67 trang 166 SBT Hình học 11
Bài tập 3.68 trang 166 SBT Hình học 10
Bài tập 3.69 trang 166 SBT Hình học 11
Bài tập 3.70 trang 167 SBT Hình học 11
Bài tập 3.71 trang 167 SBT Hình học 11
Bài tập 3.72 trang 167 SBT Hình học 11
Bài tập 3.73 trang 168 SBT Hình học 11
Bài tập 1 trang 120 SGK Hình học 11 NC
Bài tập 2 trang 120 SGK Hình học 11 NC
Bài tập 3 trang 120 SGK Hình học 11 NC
Bài tập 4 trang 120 SGK Hình học 11 NC
Bài tập 5 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC
-


Cho hình lập phương \(ABCD.EFGH\), góc giữa đường thẳng \(EG\) và mặt phẳng \((BCGF)\) là:
bởi Nguyễn Trung Thành
 26/02/2021
26/02/2021
A. 00
B. 450
C. 900
D. 300
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S. ABCD\), đáy là hình thoi tâm \(O\) và \(SA =SC, SB = SD\). Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
bởi Ha Ku
 25/02/2021
25/02/2021
A. AC.
B. SA.
C. SO.
D. SD.
Theo dõi (0) 1 Trả lời -


Cho hình lăng trụ \(ABC.A’B’C’\) với \(G\) là trọng tâm của tam giác \(A’B’C’\). Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\,\overrightarrow {AB} = \overrightarrow b ,\,\overrightarrow {AC} = \overrightarrow c \) . Vec tơ \(\overrightarrow {B'C} \) bằng:
bởi Nguyễn Vân
 26/02/2021
26/02/2021
A. \(\overrightarrow a - \overrightarrow b - \overrightarrow c \).
B. \(\overrightarrow c - \overrightarrow a - \overrightarrow b \).
C. \(\overrightarrow b - \overrightarrow a - \overrightarrow c \).
D. \(\overrightarrow a + \overrightarrow b + \overrightarrow c \).
Theo dõi (0) 1 Trả lời -


Trong không gian cho hai hình vuông \(ABCD\) và \(A’B’C’D’\) có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O’. Tứ giác CDD’C’ là hình gì?
bởi Truc Ly
 26/02/2021
26/02/2021
A. Hình bình hành.
B. Hình vuông.
C. Hình thang.
D. Hình chữ nhật.
Theo dõi (0) 1 Trả lời