Giải bài 3.43 tr 161 SBT Hình học 11
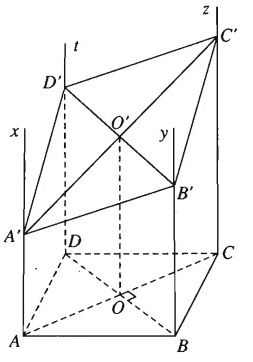
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A', B', C', D'.
a) Tứ giác A'B'C'D' là hình gì? Chứng minh rằng AA′ + CC′ = BB′ + DD′ = 2OO′.
b) Chứng minh rằng điều kiện để tứ giác A'B'C'D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).
c) Chứng minh rằng điều kiện để tứ giác A'B'C'D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
Hướng dẫn giải chi tiết
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC). Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên A′D′ // B′C′.
Tương tự, A′B′ // D′C′. Vậy A'B'C'D' là hình bình hành.
Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình với O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A'B'C'D'.
Do đó AA′ + CC′ = BB′ + DD′ = 2OO′
b) Để hình bình hành A'B'C'D' là hình thoi ta cần phải có A'C' ⊥ B'D'.
Ta có AC ⊥ BD, A'B'C'D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.
c) Để hình bình hành A'B'C'D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α).
Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A'B'C'D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3.41 trang 161 SBT Hình học 11
Bài tập 3.42 trang 161 SBT Hình học 11
Bài tập 3.44 trang 162 SBT Hình học 11
Bài tập 3.45 trang 162 SBT Hình học 11
Bài tập 3.46 trang 162 SBT Hình học 11
Bài tập 3.47 trang 162 SBT Hình học 11
Bài tập 3.49 trang 163 SBT Hình học 11
Bài tập 3.50 trang 163 SBT Hình học 11
Bài tập 3.51 trang 163 SBT Hình học 11
Bài tập 3.52 trang 163 SBT Hình học 11
Bài tập 3.53 trang 163 SBT Hình học 11
Bài tập 3.54 trang 164 SBT Hình học 11
Bài tập 3.55 trang 164 SBT Hình học 11
Bài tập 3.56 trang 164 SBT Hình học 11
Bài tập 3.57 trang 164 SBT Hình học 11
Bài tập 3.58 trang 164 SBT Hình học 11
Bài tập 3.59 trang 165 SBT Hình học 11
Bài tập 3.60 trang 165 SBT Hình học 11
Bài tập 3.61 trang 165 SBT Hình học 11
Bài tập 3.62 trang 165 SBT Hình học 11
Bài tập 3.63 trang 165 SBT Hình học 11
Bài tập 3.64 trang 165 SBT Hình học 11
Bài tập 3.65 trang 165 SBT Hình học 11
Bài tập 3.66 trang 166 SBT Hình học 11
Bài tập 3.67 trang 166 SBT Hình học 11
Bài tập 3.68 trang 166 SBT Hình học 10
Bài tập 3.69 trang 166 SBT Hình học 11
Bài tập 3.70 trang 167 SBT Hình học 11
Bài tập 3.71 trang 167 SBT Hình học 11
Bài tập 3.72 trang 167 SBT Hình học 11
Bài tập 3.73 trang 168 SBT Hình học 11
Bài tập 1 trang 120 SGK Hình học 11 NC
Bài tập 2 trang 120 SGK Hình học 11 NC
Bài tập 3 trang 120 SGK Hình học 11 NC
Bài tập 4 trang 120 SGK Hình học 11 NC
Bài tập 5 trang 120 SGK Hình học 11 NC
Bài tập 6 trang 120 SGK Hình học 11 NC
Bài tập 7 trang 121 SGK Hình học 11 NC
Bài tập 8 trang 121 SGK Hình học 11 NC
Bài tập 1 trang 122 SGK Hình học 11 NC
Bài tập 2 trang 122 SGK Hình học 11 NC
Bài tập 3 trang 122 SGK Hình học 11 NC
Bài tập 4 trang 122 SGK Hình học 11 NC
Bài tập 5 trang 122 SGK Hình học 11 NC
Bài tập 6 trang 123 SGK Hình học 11 NC
Bài tập 7 trang 123 SGK Hình học 11 NC
Bài tập 8 trang 123 SGK Hình học 11 NC
Bài tập 9 trang 123 SGK Hình học 11 NC
Bài tập 10 trang 123 SGK Hình học 11 NC
-


Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông và \(SA \bot \left( {ABCD} \right)\). Khi đó, tam giác SBC là:
bởi Đặng Ngọc Trâm
 25/02/2021
25/02/2021
A. Tam giác thường.
B. Tam giác đều.
C. Tam giác cân.
D. Tam giác vuông.
Theo dõi (0) 1 Trả lời -


Cho hình lập phương \(ABCD.A’B’C’D’\). Góc giữa hai đường thẳng \(AC\) và \(C’D’\) bằng:
bởi May May
 26/02/2021
26/02/2021
A. 00
B. 450
C. 900
D. 600
Theo dõi (0) 1 Trả lời -


Cho tứ diện \(ABCD\). Gọi \(M, N, P, Q\) lần lượt là trung điểm của \(AB, BC, CD\) và DA. Véc tơ \(\overrightarrow {MN} \) cùng với hai vec tơ nào sau đây đồng phẳng ?
bởi Song Thu
 26/02/2021
26/02/2021
A. \(\overrightarrow {MA} \,,\,\overrightarrow {MQ} \).
B. \(\overrightarrow {MD} \,,\,\overrightarrow {MQ} \).
C. \(\overrightarrow {AC} \,,\,\overrightarrow {AD} \).
D. \(\overrightarrow {MP} \,,\,\overrightarrow {CD} \).
Theo dõi (0) 1 Trả lời -


1. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước .
2. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
3. Nếu một đường thẳng và một mặt phẳng cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
4. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
A. 1
B. 2
C. 3
D. 4.
Theo dõi (0) 1 Trả lời