Giải bài 2 tr 17 sách GK Toán Hình lớp 10
Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ \( \overrightarrow{AB},\overrightarrow{BC},\overrightarrow{AC}\), theo hai vectơ sau \(\overrightarrow{u}=\overrightarrow{AK},\overrightarrow{v}=\overrightarrow{BM}\).
Hướng dẫn giải chi tiết bài 2
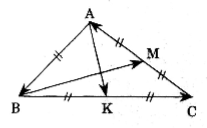
Do tính chất trung điểm nên từ giả thiết ta có:
\(\left\{ \begin{array}{l}2\overrightarrow {AK} = \overrightarrow {AB} + \overrightarrow {AC} \\2\overrightarrow {BM} = \overrightarrow {BA} + \overrightarrow {BC} \end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AB} - \overrightarrow {CA} = 2\vec u\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\ - \overrightarrow {AB} + \overrightarrow {BC} = 2\vec v\,\,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\)
Mặt khác, ta có: \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {AC} + \overrightarrow {CA} \)
\( \Leftrightarrow \,\,\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \vec 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)\)
Từ (1) và (2) ta có:
\((\overrightarrow {AB} - \overrightarrow {CA} ) + ( - \overrightarrow {AB} + \overrightarrow {BC} ) = 2\vec u + 2\vec v\)
\( \Leftrightarrow \overrightarrow {AB} - \overrightarrow {CA} - \overrightarrow {AB} + \overrightarrow {BC} = 2\vec u + 2\vec v\)
\( \Leftrightarrow - \overrightarrow {CA} + \overrightarrow {BC} = 2\vec u + 2\vec v\) (4)
Từ (2) và (3) ta có:
\( - \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = 2\vec v\)
\( \Leftrightarrow 2\overrightarrow {BC} + \overrightarrow {CA} = 2\vec v\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(5)\)
Từ (4) và (5) suy ra:
\( - \overrightarrow {AB} + \overrightarrow {BC} + 2\overrightarrow {BC} + \overrightarrow {CA} = 2\vec u + 2\vec v + 2\vec v\)
\( \Leftrightarrow 3\overrightarrow {BC} = 2\vec u + 4\vec v \Leftrightarrow \overrightarrow {BC} = \frac{2}{3}\vec u + \frac{4}{3}\vec v\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(6)\)
Từ (5) và (6) ta có:
\(\frac{4}{3}\vec u + \frac{8}{3}\vec v\, + \overrightarrow {CA} = 2\vec v \Rightarrow \overrightarrow {CA} = - \frac{4}{3}\vec u + \frac{2}{3}\vec v\,\,\,\,\,\,\,\,\,(7)\)
Từ (7) và (1), ta có được:
\(\overrightarrow {AB} + \frac{4}{3}\vec u + \frac{2}{3}\vec v = 2\vec u \Leftrightarrow \overrightarrow {AB} = \frac{2}{3}\vec u - \frac{2}{3}\vec v\)
Kết luận:
\(\overrightarrow {AB} = \frac{2}{3}\vec u - \frac{2}{3}\vec v\)
\(\overrightarrow {BC} = \frac{2}{3}\vec u + \frac{4}{3}\vec v\)
\(\overrightarrow {CA} = - \frac{4}{3}\vec u - \frac{2}{3}\vec v\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1 trang 17 SGK Hình học 10
Bài tập 3 trang 17 SGK Hình học 10
Bài tập 4 trang 17 SGK Hình học 10
Bài tập 5 trang 17 SGK Hình học 10
Bài tập 6 trang 17 SGK Hình học 10
Bài tập 7 trang 17 SGK Hình học 10
Bài tập 8 trang 17 SGK Hình học 10
Bài tập 9 trang 17 SGK Hình học 10
Bài tập 1.20 trang 31 SBT Hình học 10
Bài tập 1.21 trang 35 SBT Hình học 10
Bài tập 1.22 trang 31 SBT Hình học 10
Bài tập 1.23 trang 31 SBT Hình học 10
Bài tập 1.24 trang 31 SBT Hình học 10
Bài tập 1.25 trang 31 SBT Hình học 10
Bài tập 1.26 trang 31 SBT Hình học 10
Bài tập 1.27 trang 31 SBT Hình học 10
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC
-


Cho năm điểm trong đó không có ba điểm nào thẳng hàng. Gọi \(\Delta \) là một tam giác có ba đỉnh lấy trong năm điểm đó, hai điểm còn lại xác định một đoạn thẳng \(\theta \). Chứng minh rằng với các cánh chọn \(\Delta \) khác nhau, đường thẳng đi qua trọng tâm tam giác \(\Delta \) và trung điểm đoạn thẳng \(\theta \) luôn đi qua một điểm cố định.
bởi An Vũ
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Cho sáu điểm trong đó không có ba điểm nào thẳng hàng. Gọi \(\Delta \) là một tam giác có ba đỉnh lấy trong sáu điểm đó và \(\Delta '\) là tam giác có ba đỉnh là ba điểm còn lại. Chứng minh rằng với các cánh chọn \(\Delta \) khác nhau, các đường thẳng nối trọng tâm hai tam giác \(\Delta \) và \(\Delta '\) luôn đi qua một điểm cố định.
bởi het roi
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Cho tam giác \(ABC\) và đường thẳng \(d\). Tìm điểm \(M\) trên đường thẳng \(d\) sao cho vec tơ \(\overrightarrow u = \overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} \) có độ dài nhỏ nhất.
bởi Thùy Trang
 22/02/2021
Theo dõi (0) 1 Trả lời
22/02/2021
Theo dõi (0) 1 Trả lời -


Cho tam giác \(ABC\) và một điểm \(O\) bất kì. Chứng minh rằng với mọi điểm \(M\) ta luôn luôn tìm được ba số \(\alpha \,,\beta \,,\gamma \) sao cho \(\alpha + \beta + \gamma = 1\) và \(\overrightarrow {OM} = \alpha \overrightarrow {OA} + \beta \overrightarrow {OB} + \gamma \overrightarrow {OC} \). Nếu điểm \(M\) trùng với trọng tâm tam giác \(ABC\) thì các số \(\alpha \,,\beta \,,\gamma \) bằng bao nhiêu?
bởi Huong Hoa Hồng
 21/02/2021
Theo dõi (0) 1 Trả lời
21/02/2021
Theo dõi (0) 1 Trả lời





