Giải bài 1.23 tr 31 SBT Hình học 10
Cho tam giác ABC. Chứng minh rằng nếu \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) thì G là trọng tâm của tam giác ABC.
Hướng dẫn giải chi tiết
Gọi I là trung điểm của BC.
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GA} + 2\overrightarrow {GI} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GA} = - 2\overrightarrow {GI} \).
Từ đó suy ra ba điểm A, G, I thẳng hàng, trong đó GA = 2GI, G nằm giữa A và I.
Vậy G là trọng tâm của tam giác ABC.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.21 trang 35 SBT Hình học 10
Bài tập 1.22 trang 31 SBT Hình học 10
Bài tập 1.24 trang 31 SBT Hình học 10
Bài tập 1.25 trang 31 SBT Hình học 10
Bài tập 1.26 trang 31 SBT Hình học 10
Bài tập 1.27 trang 31 SBT Hình học 10
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC
-
Cho \(\sin a=-\dfrac{1}{5}\) và \(\pi < a < \frac{{3\pi }}{2}\). Tính \( \cos a; \tan a; \cot a \)?
bởi Nraug Hmoob CôĐơn
24/06/2020
Ln họ em voi
Theo dõi (0) 1 Trả lời -
Giải các bất phương trình sau?
bởi linh thục
19/06/2020
Giải hết 5 câu giúp em ạ tại em không biệt giải sao ạ
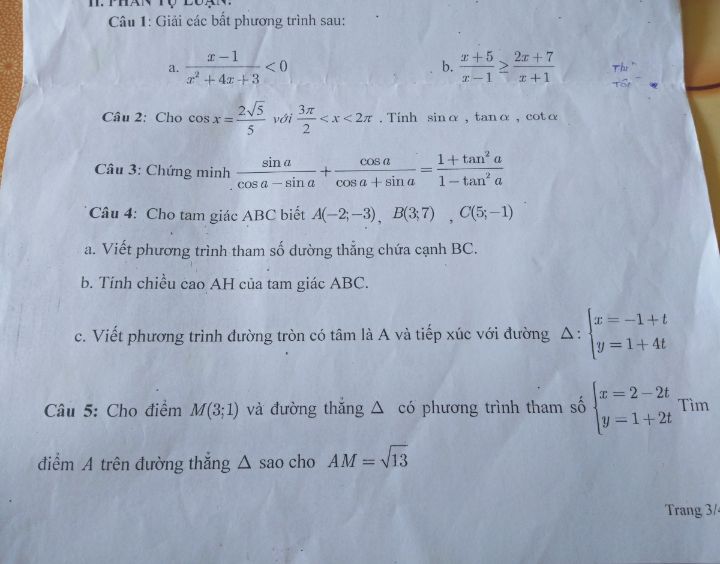Theo dõi (2) 6 Trả lời -
Cho tam giác ABC tìm tập hợp điểm thỏa mãn:
bởi Hồng Nhung
21/04/2020
Theo dõi (0) 0 Trả lời -
Cho hình bình hành abcd, có ac=10, bd=8.tính tích vô hướng của ab.ad?Theo dõi (0) 0 Trả lời
