Giải bài 1.32 tr 32 SBT Hình học 10
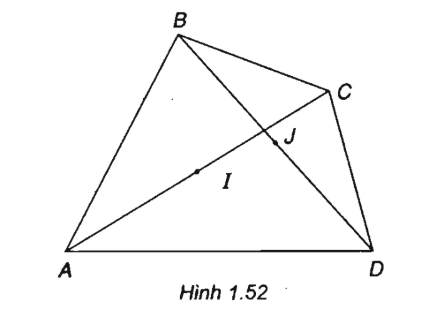
Cho tứ giác ABCD. Gọi I và J lần lượt là trung điểm của hai đường chéo AC và BD. Chứng minh \(\overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {IJ} \).
Hướng dẫn giải chi tiết
Ta có :
\(\begin{array}{l}
\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AB} + \overrightarrow {BJ} \\
\overrightarrow {IJ} = \overrightarrow {IC} + \overrightarrow {CD} + \overrightarrow {DJ}
\end{array}\)
Cộng từng vế hai đẳng thức trên ta được
\(2\overrightarrow {IJ} = \left( {\overrightarrow {IA} + \overrightarrow {IC} } \right) + \left( {\overrightarrow {BJ} + \overrightarrow {DJ} } \right) + \overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AB} + \overrightarrow {CD} \)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC
-


Chứng minh vt AB+vt CD=vt AD+vt CB
bởi Phạm Phú Lộc Nữ
 22/10/2018
22/10/2018
cho 4 điểm A,B C, D bất kì. Gọi I,J là trung điểm của AB, CD và M là 1 điểm tùy ý. Chứng minh
a) AB→ +CD →= AD→+ CB→
b) 2IJ→ = AC→ + BD→ = AD→ + BC→
c) Định điểm O sao cho : OA→ + OB→ + OC→+ OD→ = 0→
Theo dõi (0) 1 Trả lời -


Chứng minh I,J,K thẳng hàng biết 2vtIA+3vtIB=vt 0
bởi Quế Anh
 05/11/2018
05/11/2018
Cho tam giác ABC
a) dựng các điểm I,J thoả \(2\overrightarrow{IA}+3\overrightarrow{IB}=\overrightarrow{0},\overrightarrow{JA}=2\overrightarrow{JC.}\)
Tính vecto IJ theo vectoAB,vectoAC (không cần làm)
b) gọi P,Q là trung điểm BI,CJ. Chứng minh \(\overrightarrow{PQ}=\dfrac{1}{2}\left(\overrightarrow{BJ}+\overrightarrow{IC}\right)\)
(Không cần làm)
c) gọi K thoả vectoBK=(4/7)vectoBC. CMR I,J,K thẳng hàng
Mình chỉ cần câu c thôi
Theo dõi (0) 3 Trả lời -


cho tam giác ABC có G là trọng tâm H đối xứng với B qua G , M là trung điểm của BC , chứng minh :
\(\overrightarrow{MH}=\dfrac{1}{6}\overrightarrow{AC}-\dfrac{5}{6}\overrightarrow{AB}\)
Theo dõi (0) 1 Trả lời -


Cm vtAA'+vtBB'+vtCC'=3vtGG' biết G,G' là trong tâm tam giác ABC, A'B'C'
bởi Nguyễn Hạ Lan
 06/11/2018
06/11/2018
Cho tam giác ABC và A'B'C', có trọng tâm lần lượt là G, G’ CMR: \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=3\overrightarrow{GG'}\)
Theo dõi (0) 1 Trả lời