Giải bài 1.35 tr 32 SBT Hình học 10
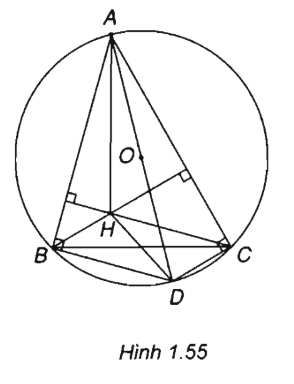
Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O.
a) Chứng minh tứ giác HCDB là hình bình hành.
b) Chứng minh:
\(\begin{array}{l}
\overrightarrow {HA} + \overrightarrow {HD} = 2\overrightarrow {HO} ;\\
\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \\
\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH}
\end{array}\)
c) Gọi G là trọng tâm tam giác ABC.
Chứng minh \(\overrightarrow {OH} = 3\overrightarrow {OG} \)
Từ đó có kết luận gì về ba điểm O, H, G.
Hướng dẫn giải chi tiết
a) Vì AD là đường kính của đường tròn tâm O nên BD⊥AB, DC⊥AC.
Ta có CH⊥AB, BH⊥Anên suy ra CH//BD và BH//DC.
Vậy tứ giác HCDB là hình bình hành.
b) Vì O là trung điểm của nên \(\overrightarrow {HA} + \overrightarrow {HD} = 2\overrightarrow {HO} \) (1)
Vì tứ giác HCDB là hình bình hành nên ta có \(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \) (2)
Từ (1) và (2) suy ra: \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \) (3)
Theo quy tắc ba điểm, từ (3) suy ra \(\overrightarrow {HO} + \overrightarrow {OA} + \overrightarrow {HO} + \overrightarrow {OB} + \overrightarrow {HO} + \overrightarrow {OC} = 2\overrightarrow {OH} \)
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \) (4).
c) G là trọng tâm của tam giác .
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \).
Từ (4) suy ra \(\overrightarrow {OH} = 3\overrightarrow {OG} \). Vậy ba điểm O, H, G thẳng hàng.
Nhận xét :
Trong một tam giác trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O thẳng hàng.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC
-


CM a.vt IA+b.vt IB+c. IC=vt 0 trong đó a, b, c là độ dài các cạnh tam giác ABC
bởi Phan Thị Trinh
 02/10/2018
02/10/2018
CÁC BẠN GIÚP MÌNH VỚI, MÌNH GỬI CÂU HỎI MÀ KHÔNG AI TRẢ LỜI!!!
Cho \(\Delta ABC\) có \(I\) là tâm đường tròn nội tiếp
CMR: \(a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\overrightarrow{0}\)
Trong đó \(a,b,c\) là độ dài các cạnh \(\Delta ABC\) (cạnh đối diện \(\widehat{A}\) là cạnh \(a\) ...)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC. M, D lần lượt là trung điểm AB, BC. N trên cạnh AC sao cho CN = 2NA. Lấy K là trung điểm của MN. Phân tích vecto KD theo 2 vecto AB và AC.
Theo dõi (0) 1 Trả lời -


cho \(\Delta ABC,M,N\) thoả mãn \(3\overrightarrow{MA}\) +\(4\overrightarrow{MB}\) =0 ; \(\overrightarrow{CN}=\frac{1}{2}\overrightarrow{BC}\) . G là trọng tâm\(\Delta ABC\)
a; cm M , G , N thẳng hàng
b; Tính \(\overrightarrow{AC}\) theo \(\overrightarrow{AG}\) và \(\overrightarrow{AN}\) . AG cắt GN tại B. Tính \(\frac{\overrightarrow{BA}}{\overrightarrow{BC}}\) ?
Theo dõi (0) 1 Trả lời -


cho tam giác ABC gọi D,I là các điểm đc xác định bởi
3DB - 2DC= 0
IA + 3IB -2IC = 0
a, biểu diễn AD theo hai vector AB và AC
b, chứng minh ba điểm I, A, D thẳng hàng
Theo dõi (0) 1 Trả lời