Giải bài 1.29 tr 32 SBT Hình học 10
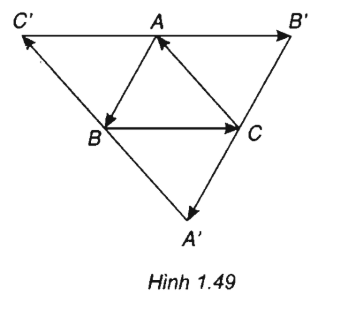
Cho tam giác ABC. Dựng \(\overrightarrow {AB'} = \overrightarrow {BC} ,\overrightarrow {CA'} = \overrightarrow {AB} \) và \(\overrightarrow {BC'} = \overrightarrow {CA} \).
a) Chứng minh rằng A là trung điểm của B′C′.
b) Chứng minh các đường thẳng AA′, BB′ và CC′ đồng quy.
Hướng dẫn giải chi tiết
a) \(\overrightarrow {BC'} = \overrightarrow {CA} \Rightarrow \) Tứ giác ACBC′ là hình bình hành \( \Rightarrow \overrightarrow {AC'} = \overrightarrow {CB} \).
\(\overrightarrow {AB'} + \overrightarrow {AC'} = \overrightarrow {BC} + \overrightarrow {CB} = \overrightarrow {BB} = \overrightarrow 0 \Rightarrow A\) là trung điểm của B′C′.
b) Vì tứ giác ACBC′ là hình bình hành nên CC′ chứa trung tuyến của tam giác ABC xuất phát từ đỉnh C.
Tương tự như vậy với AA′, BB′. Do đó AA′, BB′, CC′ đồng quy tại trọng tâm G của tam giác ABC.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.27 trang 31 SBT Hình học 10
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC
-


Chứng minh vtHA +vtHB + vt HC =2vtHO
bởi Bánh Mì
 16/10/2018
16/10/2018
cho tam giác ABC nội tiếp đường tròn O .Gọi H là trực tâm tam giác ABC và AD là đường kính của đường tròn 0 chứng minh vtHA +vtHB + vt HC =2vtHO
Theo dõi (0) 1 Trả lời -


Giúp mình câu này với!
Cho tam giác ABC. Tập hợp những điểm M sao cho: \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MC} +\overrightarrow{MB}\right|\)là:
A. M nằm trên đường trung trực của BC.
B. M nằm trên đường tròn tâm I, R = 2AB với I nằm trên cạnh AB sao cho IA = 2IB.
C. M nằm trên đường trung trực của IJ với I, J lần lượt là trung điểm của AB và BC.
D. M nằm trên đường tròn tâm I, R = 2AC với I nằm trên cạnh AB sao cho IA = 2IB.
Theo dõi (0) 1 Trả lời -


Chứng minh 2(vt AB+vt AI+vt FA+ vt DA)=3 vt DB
bởi Co Nan
 22/10/2018
22/10/2018
Cho 4 điểm A, B, C, D; I, F lần lượt là trung điểm BC, CD. Chứng minh: \(2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{FA}+\overrightarrow{DA}\right)=3\overrightarrow{DB}\)
Theo dõi (0) 1 Trả lời -


Chứng minh vt OC=(3 vt OA)/5+(2 vt OB)/5
bởi Hoai Hoai
 22/10/2018
22/10/2018
Trên trục x'Ox cho ba điểm A,B,C thoả mãn \(\dfrac{\overrightarrow{AC}}{2}=\dfrac{\overrightarrow{CB}}{3}CMR:\overrightarrow{OC}=\dfrac{3\overrightarrow{OA}}{5}+\dfrac{2\overrightarrow{OB}}{5}\)
Theo dõi (0) 1 Trả lời