Giải bài 1.28 tr 32 SBT Hình học 10
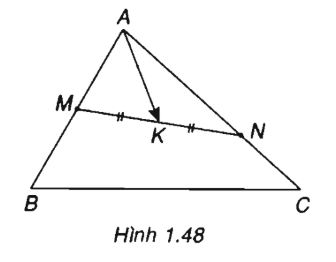
Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2NC. Gọi K là trung điểm của MN. Phân tích vec tơ \(\overrightarrow {AK} \) theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
Hướng dẫn giải chi tiết
Ta có \(\overrightarrow {AK} = \frac{1}{2}\left( {\overrightarrow {AM} + \overrightarrow {AN} } \right) = \frac{1}{2}\left( {\frac{1}{2}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} } \right) = \frac{1}{4}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.26 trang 31 SBT Hình học 10
Bài tập 1.27 trang 31 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC
-


Chứng minh góc BIC =90 độ biết I là giao điểm AM và CN
bởi Phan Quân
 13/10/2018
13/10/2018
Cho tam giác ABC đều cạnh a. Lấy hai điểm M,N thoả \(\overrightarrow{BM}=\dfrac{1}{3}\overrightarrow{BC};\overrightarrow{AN}=\dfrac{1}{3}\overrightarrow{AB}\)
Gọi I là giao điểm AM và CN. Chứng minh: \(\widehat{BIC}=90^0\)
Theo dõi (0) 1 Trả lời -


Chứng minh 3vt DG= vt DA+ vt DB+ vt DC
bởi Nguyễn Thị Trang
 13/10/2018
13/10/2018
BÀi 1: cho hình bình hành ABCD có tâm O . Gọi I là trung điểm BC và G là trọng tâm ΔABC. CM:
a)\(2\overrightarrow{AI}=2\overrightarrow{AO}+\overrightarrow{AB}\)
b)\(3\overrightarrow{DG}=\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\)
Theo dõi (0) 1 Trả lời -


Tìm x để A, I, H thẳng hàng
bởi May May
 16/10/2018
16/10/2018
cho △ABC và M, N là các điểm thỏa: AM→ = \(\dfrac{2}{3}\)AB→, AN→ = \(\dfrac{2}{3}\) AC→. Gọi I là trung điểm MN và H là điểm thỏa
BH→ = xBC→
a) tính AI→, AH→ theo AB→, AC→
b)Tìm x đề A,I ,H thẳng hàng
Theo dõi (0) 1 Trả lời -


cho tam giác ABC , M là điểm thỏa mãn\(\overrightarrow{|2MA}+\overrightarrow{MB|}=\overrightarrow{|4MB}-\overrightarrow{MC}|\)
Tìm tập hợp các điểm M
Theo dõi (0) 1 Trả lời