Giải bài 1.26 tr 31 SBT Hình học 10
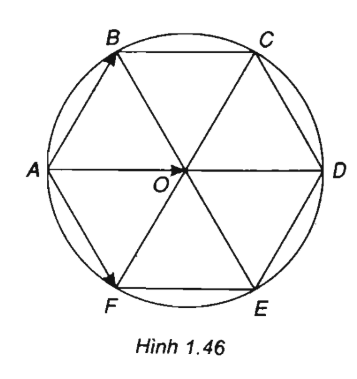
Cho lục giác đều ABCDEF tâm O có cạnh a.
a) Phân tích vec tơ \(\overrightarrow {AD} \) theo hai vec tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AF} \).
b) Tính độ dài của vec tơ \(\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} \) theo aa.
Hướng dẫn giải chi tiết
a) \(\overrightarrow {AD} = 2\overrightarrow {AO} = 2\left( {\overrightarrow {AB} + \overrightarrow {AF} } \right) = 2\overrightarrow {AB} + 2\overrightarrow {AF} \)
b)
\(\begin{array}{l}
\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) = \frac{1}{2}\overrightarrow {AC} \\
\Rightarrow \left| {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} } \right| = \frac{1}{2}\left| {\overrightarrow {AC} } \right|
\end{array}\)
Dễ thấy tam giác OAB đều có \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\)
Tứ giác AOCB là hình thoi nên \(AC = 2AH = a\sqrt 3 \)
Vậy \(\left| {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} } \right| = \frac{1}{2}\left| {\overrightarrow {AC} } \right| = \frac{{a\sqrt 3 }}{2}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.24 trang 31 SBT Hình học 10
Bài tập 1.25 trang 31 SBT Hình học 10
Bài tập 1.27 trang 31 SBT Hình học 10
Bài tập 1.28 trang 32 SBT Hình học 10
Bài tập 1.29 trang 32 SBT Hình học 10
Bài tập 1.30 trang 32 SBT Hình học 10
Bài tập 1.31 trang 32 SBT Hình học 10
Bài tập 1.32 trang 32 SBT Hình học 10
Bài tập 1.33 trang 32 SBT Hình học 10
Bài tập 1.34 trang 32 SBT Hình học 10
Bài tập 1.35 trang 32 SBT Hình học 10
Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 22 trang 24 SGK Toán 10 NC
Bài tập 23 trang 24 SGK Hình học 10 NC
Bài tập 24 trang 24 SGK Hình học 10 NC
Bài tập 25 trang 24 SGK Hình học 10 NC
Bài tập 26 trang 24 SGK Hình học 10 NC
-


Chứng minh M,G,N thẳng hàng biết 3MA+4MB=0, CN=1/2BC, G là trọng tâm tam giác ABC
bởi Vũ Quỳnh
 24/09/2018
24/09/2018
Cho Δ ABC. M,N là 2 điểm định bởi 3MA ↑ + 4MB ↑ = 0 ↑, CN ↑ =½ BC ↑. G là trọng tâm Δ ABC.
a) Chứng minh M,G,N thẳng hàng.
b) Tính AC↑ theo AG ↑ và AN ↑.
c) Gọi P là giao điểm của AC và GN. Tính PA / PC?
nghi chú :
↑: vectơ.
Theo dõi (0) 1 Trả lời -


Khẳng định nào sau đây sai vecto MN = MD + CN + DC ?
bởi Huyền Trân
 13/09/2018
13/09/2018
cho hình thang ABCD có đáy là AB và CD.Gọi M và N lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai
a. vecto MN = MD + CN + DC
b. vecto MN = AB - MD + BN
c. vecto MN = 1/2 (AB + DC)
d. vecto MN = 1/2 (AD + BC)
Theo dõi (0) 3 Trả lời -


Tính độ dài của vecto v=vectoBA +vectoBC
bởi Nguyễn Trà Giang
 13/10/2018
13/10/2018
Tam giác ABC đều. I là trung điểm AC.
a. Xác định M sao cho vectoAB+vectoIM=vectoIC
b. Tính độ dài của vecto v=vectoBA +vectoBC
Theo dõi (0) 1 Trả lời -


Tìm đẳng thức đúng biết D là trung điểm CM
bởi minh thuận
 13/10/2018
13/10/2018
Câu 1 : Cho tam giác ABC có trung tuyến BM và trọng tâm G. Khi đó \(\overrightarrow{BG}\) =
A. \(\overrightarrow{BA}\) + \(\overrightarrow{BC}\)
B. \(\dfrac{1}{2}\) . ( \(\overrightarrow{BA}\) + \(\overrightarrow{BC}\) )
C. \(\dfrac{1}{3}\) . \(\overrightarrow{BA}\) + \(\overrightarrow{BC}\)
D. \(\dfrac{1}{3}\) . ( \(\overrightarrow{BA}\) + \(\overrightarrow{BC}\) )
Câu 2 : Gọi CM là trung tuyến của tam giác ABC và D là trung điểm CM. Đẳng thức nào sau đây đúng ?
A. \(\overrightarrow{DA}\) + \(\overrightarrow{DB}\) + 2. \(\overrightarrow{DC}\) = 0
B. \(\overrightarrow{DA}\) + \(\overrightarrow{DC}\) + 2. \(\overrightarrow{DB}\) = 0
C. \(\overrightarrow{DA}\) + \(\overrightarrow{DB}\) + 2. \(\overrightarrow{CD}\) = 0
D. \(\overrightarrow{DC}\) + \(\overrightarrow{DB}\) + 2. \(\overrightarrow{DA}\) = 0
Theo dõi (0) 1 Trả lời