Phần hướng dẫn giải bài tập Hình học 11 Ôn tập chương I Phép dời hình và Phép đồng dạng trong mặt phẳng sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Hình học 11 Cơ bản và Nâng cao.
-
Bài tập 1 trang 33 SGK Hình học 11
Thế nào là một phép biến hình, phép dời hình, phép đồng dạng? Nêu mối liên hệ giữa phép dời hình và phép đồng dạng.
-
Bài tập 2 trang 33 SGK Hình học 11
a) Hãy kể các phép dời hình đã học.
b) Phép đồng dạng có phải là phép vị tự không?
-
Bài tập 3 trang 33 SGK Hình học 11
Hãy nêu một số tính chất đúng với phép dời hình mà không đúng đối với phép đồng dạng.
-
Bài tập 4 trang 34 SGK Hình học 11
Cho vecto \(\vec v\), đường thẳng d vuông góc với giá của \(\vec v\). Gọi d’ là ảnh của d qua phép tịnh tiến theo vecto \(\frac{1}{2}\vec v\). Chứng minh rằng phép tịnh tiến theo vecto \(\vec v\) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng d và d’.
- VIDEOYOMEDIA
-
Bài tập 1 trang 34 SGK Hình học 11
Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác AOF.
a) Qua phép tịnh tiến theo vecto \(\overrightarrow {AB} \)
b) Qua phép đối xứng qua đường thẳng BE
c) Qua phép quay tâm O góc \({120^0}\)
-
Bài tập 2 trang 34 SGK Hình học 11
Trong mặt phẳng toạ độ Oxy cho điểm A(-1; 2) và đường thẳng d có phương trình \(3x + y + 1 = 0.\) Tìm ảnh của A và d.
a) Qua phép tịnh tiến theo vecto \(\vec v = (2;1)\)
b) Qua phép đối xứng qua trục Oy
c) Qua phép đối xứng qua gốc toạ độ;
d) Qua phép quay tâm O góc \({90^0}\)
-
Bài tập 3 trang 34 SGK Hình học 11
Trong mặt phẳng toạ độ Oxy, cho đường tròn tâm I(3;- 2), bán kính 3.
a) Viết phương trình của đường tròn đó.
b) Viết phương trình của đường tròn (I; 3) qua phép tịnh tiến theo vecto \(\vec v = ( - 2;1)\) .
c) Viết phương trình ảnh của đường tròn (I; 3) qua phép đối xứng qua trục Ox.
d) Viết phương trình ảnh của đường tròn (I; 3) qua phép đối xứng qua gốc toạ độ.
-
Bài tập 4 trang 34 SGK Hình học 11
Thế nào là hình bằng nhau, hai hình đồng dạng với nhau? Cho ví dụ?
-
Bài tập 5 trang 34 SGK Hình học 11
Cho hai điểm phân biệt A, B và đường thẳng d. Hãy tìm một phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm, phép quay, phép vị tự thoả mãn một trong các tính chất sau:
a) Biến A thành chính nó;
b) Biến A thành B
c) Biến d thành chính nó.
-
Bài tập 6 trang 34 SGK Hình học 11
Nêu cách tìm tâm vị tự của hai đường tròn.
-
Bài tập 5 trang 35 SGK Hình học 11
Cho hình chữ nhật ABCD. Gọi O là tâm đối xứng của nó. Gọi I, F, J, E lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tìm ảnh của tam giác AEO qua phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng qua đường thẳng IJ và phép vị tự tâm B, tỉ số 2.
-
Bài tập 6 trang 35 SGK Hình học 11
Trong mặt phẳng toạ độ Oxy, cho đường tròn tâm I(1; -3), bán kính 2. Viết phương trình ảnh của đường tròn (I; 2) qua phép đồng dạng có được từ việc thực hiện liên tiếp phép vị tự tâm O tỉ số 3 và phép đối xứng qua trục Ox.
-
Bài tập 7 trang 35 SGK Hình học 11
Cho hai điểm A, B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O), dựng hình bình hành MABN. Chứng minh rằng điểm N thuộc một đường tròn xác định.
-
Bài tập 1 trang 35 SGK Hình học 11
Trong các phép biến hình sau, phép nào không phải là phép dời hình?
(A) Phép chiếu vuông góc lên một đường thẳng;
(B) Phép đồng nhất
(C) Phép vị tự tỉ số (-1)
(D) Phép đối xứng trục
-
Bài tập 2 trang 35 SGK Hình học 11
Trong các mệnh đề sau, mệnh đề nào sai"
(A) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó;
(B) Phép đối xứng trục biến đường thẳng thành đường thẳng song song hoặc trùng với nó;
(C) Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó;
(D) Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
-
Bài tập 3 trang 35 SGK Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(2x - y + 1 = 0.\) Để phép tịnh tiến theo vecto \(\vec v\) biến d thành chính nó thì \(\vec v\) phải là vecto nào trong các vecto sau?
(A) \(\vec v = (2;\,\,1)\) (B) \(\vec v = (2;\,\, - 1)\)
(C) \(\vec v = (1;\,\,2)\) (D)\(\vec v = ( - 1;\,\,2)\)
-
Bài tập 4 trang 36 SGK Hình học 11
Trong mặt phẳng toạ độ Oxy, cho \(\vec v = (2; - 1)\) và điểm \(M( - 3;2).\) Ảnh của điểm M qua phép tịnh tiến theo vecto \(\vec v\) là điểm có toạ độ nào trong các toạ độ sau?
(A) (5;3) (B) (1; 1)
(C) (-1; 1) (D) (1; -1)
-
Bài tập 5 trang 36 SGK Hình học 11
Trong mặt phẳng toạ độ Oxy cho đường thẳng d có phương trình: \(3x - 2y + 1 = 0.\) Ảnh của đường thẳng d qua phép đối xứng trục Ox có phương trình là:
(A) \(3x + 2y + 1 = 0\) (B) \( - 3x + 2y + 1 = 0\)
(C) \(3x + 2y - 1 = 0\) (D) \(3x - 2y + 1 = 0\)
-
Bài tập 6 trang 36 SGK Hình học 11
Trong mặt phẳng toạ độ Oxy cho đường thẳng d có phương trình: \(3x - 2y - 1 = 0.\) Ảnh của đường thẳng d qua phép đối xứng tâm O có phương trình là:
(A) \(3x + 2y + 1 = 0\) (B) \( - 3x + 2y - 1 = 0\)
(C) \(3x + 2y - 1 = 0\) (D) \(3x - 2y - 1 = 0\)
-
Bài tập 7 trang 36 SGK Hình học 11
Trong các mệnh đề sau, mệnh đề nào sai?
(A) Có một phép tịnh tiến biến mọi điểm thành chính nó;
(B) Có một phép đối xứng trục biến mọi điểm thành chính nó
(C) Có một phép quay biến mọi điểm thành chính nó;
(D) Có một phép vị tự biến mọi điểm thành chính nó.
-
Bài tập 8 trang 36 SGK Hình học 11
Hình vuông có mấy trục đối xứng?
(A) 1
(B) 2
(C) 4
(D) Vô số
-
Bài tập 9 trang 36 SGK Hình học 11
Trong các hình sau, hình nào có vô số tâm đối xứng?
(A) Hai đường thẳng cắt nhau
(B) Đường elip
(C) Hai đường thẳng song song
(D) Hình lục giác đều
-
Bài tập 10 trang 36 SGK Hình học 11
Trong các mệnh đề sau, mệnh đề nào sai?
(A) Hai đường thẳng bất kỳ luôn luôn đồng dạng
(B) Hai đường tròn bất kỳ luôn đồng dạng
(C) Hai hình vuông bất kỳ luôn đồng dạng
(D) Hai chữ nhật bất kỳ luôn đồng dạng.
-
Bài tập 1.31 trang 37 SBT Hình học 11
Trong mặt phẳng Ox cho đường thẳng d có phương trình 3x−5y+3 = 0 và vectơ \(\overrightarrow v = \left( {2;3} \right)\). Hãy viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến theo vectơ \(\overrightarrow v\).
-
Bài tập 1.32 trang 37 SBT Hình học 11
Cho hình bình hành ABCD có AB cố định, đường chéo AC có độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.
-
Bài tập 1.33 trang 37 SBT Hình học 11
Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.
-
Bài tập 1.34 trang 37 SBT Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−2y−6 = 0
a) Viết phương trình của đường thẳng d1 là ảnh của d qua phép đối xứng qua trục Oy.
b) Viết phương trình của đường thẳng d2 là ảnh của d qua phép đối xứng qua đường thẳng Δ có phương trình x+y−2 = 0.
-
Bài tập 1.35 trang 37 SBT Hình học 10
Cho đường tròn (C) và hai điểm cố định phân biệt A,B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A,B), ta xét điểm N sao cho AMBN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.
-
Bài tập 1.36 trang 37 SBT Hình học 11
Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và r, (R>r). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D sao cho CD = 3AB.
-
Bài tập 1.37 trang 37 SBT Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x+y−2 = 0. Hãy viết phương trình của đường thẳng d′ là ảnh của d qua phép quay tâm O góc 45∘.
-
Bài tập 1.38 trang 38 SBT Hình học 11
Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng 60ο. Chứng minh rằng tứ giác MNPQ là một hình thang cân.
-
Bài tập 1.39 trang 38 SBT Hình học 11
Gọi A′, B′, C′ tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng \(\overrightarrow {A'B'} .\overrightarrow {A'C'} = {k^2}\overrightarrow {AB.} \overrightarrow {AC} \).
-
Bài tập 1.40 trang 38 SBT Hình học 11
Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu \(\overrightarrow {AB} = p\overrightarrow {AC} \) thì \(\overrightarrow {A'B'} = p\overrightarrow {A'C'} \), trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.
-
Bài tập 1.41 trang 38 SBT Hình học 11
Trong mặt phẳng Oxy xét phép biến hình F biến mỗi điểm M(x;y) thành M′(2x−1;−2y+3). Chứng minh F là một phép đồng dạng.
-
Bài tập 1.42 trang 38 SBT Hình học 11
Dựng tam giác BAC vuông cân tại A có C là một điểm cho trước, còn hai đỉnh A, B lần lượt thuộc hai đường thẳng a, b song song với nhau cho trước.
-
Bài tập 1.43 trang 38 SBT Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d: 2x−y+6 = 0. Viết phương trình đường thẳng d′ là ảnh của d qua phép đối xứng tâm I(−2;1).
-
Bài tập 1.44 trang 38 SBT Hình học 11
Trong mặt phẳng Oxy cho đường tròn (C): x2+y2+2x−4y−11 = 0. Tìm phép tịnh tiến biến (C) thành (C′): (x−10)2+(y+5)2 = 16
-
Bài tập 1.45 trang 38 SBT Hình học 11
Trong mặt phẳng Oxy cho hai đường thẳng d: x−5y+7 = 0 và d′: 5x−y−13 = 0. Tìm phép đối xứng qua trục biến d thành d′.
-
Bài tập 1.46 trang 38 SBT Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−y−3 = 0. Viết phương trình đường thẳng d1 là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm I(−1;2) và phép quay tâm O góc quay −90∘.
-
Bài tập 1.47 trang 38 SBT Hình học 11
Trong mặt phẳng Oxy cho đường tròn (C): (x−1)2+(y−2)2 = 9. Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép đối xứng trục d: x = 1.
-
Bài tập 1.48 trang 38 SBT Hình học 11
Trong mặt phẳng Oxy cho đường tròn (C):(x−1)2+(y−2)2 = 9. Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép quay Q(0;−900) với O là gốc tọa độ.
-
Bài tập 1.49 trang 39 SBT Hình học 11
Trong mặt phẳng (Oxy) cho điểm A(2;5). Phép tịnh tiến theo véc tơ \(\vec v = \left( {1;2} \right)\) biến A thành điểm có tọa độ
A. (3;1) B. (1;6)
C. (3;7) D. (4;7)
-
Bài tập 1.50 trang 39 SBT Hình học 11
Trong mặt phẳng (Oxy) cho điểm A(4;5). Qua phép tịnh tiến theo véc tơ \(\vec v = \left( {2;1} \right)\), A là ảnh của điểm có tọa độ
A. (3;1) B. (1;6)
C. (4;7) D. (2;4)
-
Bài tập 1.51 trang 39 SBT Hình học 11
Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
-
Bài tập 1.52 trang 39 SBT Hình học 11
Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
-
Bài tập 1.53 trang 39 SBT Hình học 11
Có bao nhiêu phép tịnh tiến biến một hình vuông thành chính nó?
A. Không có B. Chỉ có một
C. Chỉ có bốn D. Vô số
-
Bài tập 1.54 trang 39 SBT Hình học 11
Trong mặt phẳng (Oxy) cho điểm M(2;3), ảnh của M qua phép đối xứng trục Ox có tọa độ
A. (3;2) B. (2;−3)
C. (3;−2) D. (−2;3)
-
Bài tập 1.55 trang 39 SBT Hình học 11
Trong mặt phẳng (Oxy) cho điểm M(2;3), qua phép đối xứng trục Oy thì M là ảnh của điểm có tọa độ
A. (3;2) B. (2;−3)
C. (3;−2) D. (−2;3)
-
Bài tập 1.56 trang 39 SBT Hình học 11
Trong mặt phẳng (Oxy) cho điểm M(2;3), ảnh của M qua phép đối xứng trục là đường thẳng x−y = 0 có tọa độ
A. (3;2) B. (2;−3)
C. (3;−2) D. (−2;3)
-
Bài tập 1.57 trang 39 SBT Hình học 11
Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
-
Bài tập 1.58 trang 39 SBT Hình học 11
Khẳng định nào sau đây là đúng?
A. Đường tròn là hình có vô số trục đối xứng
B. Một hình có vô số trục đối xứng thì hình đó phải là đường tròn.
C. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm những đường tròn đồng tâm.
D. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm hai đường thẳng vuông góc.
-
Bài tập 1.59 trang 40 SBT Hình học 11
Trong mặt phẳng Oxy, cho hai điểm I(1;2) và M(3;−1). Ảnh của điểm M qua phép đối xứng tâm I có tọa độ
A. (2;1) B. (−1;5)
C. (−1;3) D. (5;−4)
-
Bài tập 1.60 trang 40 SBT Hình học 11
Trong mặt phẳng (Oxy) cho đường thẳng Δ có phương trình x = 2. Ảnh của Δ qua phép đối xứng tâm O là đường thẳng
A. x = −2 B. y = 2
C. x = 2 D. y = −2
-
Bài tập 1.61 trang 40 SBT Hình học 11
Khẳng định nào sau đây là đúng?
A. Phép đối xứng tâm không có điểm nào biến thành chính nó.
B. Phép đối xứng tâm có đúng một điểm biến thành chính nó.
C. Có phép đối xứng tâm có hai điểm biến thành chính nó.
D. Có phép đối xứng tâm có vô số điểm biến thành chính nó.
-
Bài tập 1.62 trang 40 SBT Hình học 11
Trong mặt phẳng Oxy, cho đường thẳng Δ có phương trình x−y+4 = 0. Đường thẳng Δ là ảnh qua một phép đối xứng tâm của đường thẳng
A. 2x+y−4 = 0
B. x+y−1 = 0
C. 2x−2y+1 = 0
D. 2x+2y−3 = 0
-
Bài tập 1.63 trang 40 SBT Hình học 11
Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
-
Bài tập 1.64 trang 40 SBT Hình học 11
Trong mặt phẳng Oxy cho điểm M(1;1). Ảnh của M qua phép quay tâm O, góc quay 450 có tọa độ
A. (−1;1) B. (1;0)
C. \(\left( {\sqrt 2 ;0} \right)\) D. \(\left( {0;\sqrt 2 } \right)\)
-
Bài tập 1.65 trang 40 SBT Hình học 11
Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc α, 0 ≤ α< 2π biến tam giác trên thành chính nó?
A. Chỉ có một B. Chỉ có hai
C. Chỉ có ba D. Chỉ có bốn
-
Bài tập 1.66 trang 40 SBT Hình học 11
Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc α, 0 ≤ α < 2π, biến hình vuông trên thành chính nó?
A. Chỉ có một B. Chỉ có hai
C. Chỉ có ba D. Chỉ có bốn
-
Bài tập 1.67 trang 41 SBT Hình học 11
Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc α, 0 ≤ α ≤ 2π, biến hình chữ nhật trên thành chính nó?
A. Không có B. Chỉ có hai
C. Chỉ có ba D. Chỉ có bốn
-
Bài tập 1.68 trang 41 SBT Hình học 11
Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc α ≠ 2kπ, k là một số nguyên?
A. Không có B. Chỉ có một
C. Chỉ có hai D. Vô số
-
Bài tập 1.69 trang 41 SBT Hình học 11
Trong mặt phẳng Oxy cho điểm M(2;1). Điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo véc tơ \(\vec v = \left( {2;3} \right)\) được biến thành điểm có tọa độ
A. (1;3) B. (2;0)
C. (0;2) D. (4;4)
-
Bài tập 1.70 trang 41 SBT Hình học 11
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x−1)2+(y+2)2 = 4. Đường tròn (C) qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo véc tơ \(\vec v = \left( {2;3} \right)\) được biến thành đường tròn có phương trình
A. x2+y2 = 4
B. (x−2)2+(y−6)2 = 4
C. (x−2)2+(y−3)2 = 4
D. (x−1)2+(y−1)2 = 4
-
Bài tập 1.71 trang 41 SBT Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x+y−2 = 0. Đường thẳng d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo véc tơ \(\overrightarrow v = \left( {3;2} \right)\) được biến thành đường thẳng có phương trình
A. 3x+3y − 2 = 0
B. x−y+2 = 0
C. x+y+2 = 0
D. x+y - 3 = 0
-
Bài tập 1.72 trang 41 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Thực hiện liên tiếp hai phép tịnh tiến sẽ được một phép tịnh tiến.
B. Thực hiện liên tiếp hai phép đối xứng trục sẽ được một phép đối xứng trục.
C. Thực hiện liên tiếp phép đối xứng qua tâm và phép đối xứng trục sẽ được một phép đối xứng qua tâm.
D. Thực hiện liên tiếp phép quay và phép tịnh tiến sẽ được một phép tịnh tiến.
-
Bài tập 1.73 trang 41 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Có một phép tịnh tiến theo véc tơ khác không biến mọi điểm thành chính nó.
B. Có một phép đối xứng trục biến mọi điểm thành chính nó.
C. Có một phép đối xứng tâm biến mọi điểm thành chính nó.
D. Có một phép quay biến mọi điểm thành chính nó.
-
Bài tập 1.74 trang 41 SBT Hình học 11
Trong mặt phẳng Oxy cho điểm M(−2;4). Phép vị tự tâm O tỉ số k = −2 biến M thành điểm có tọa độ
A. (−8;4) B. (−4;−8)
C. (4;−8) D. (4;8)
-
Bài tập 1.75 trang 42 SBT Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x+y−3 = 0. Phép vị tự tâm O tỉ số k = 2 biến d thành đường thẳng có phương trình
A. 2x+y+3 = 0
B. 2x+y−6 = 0
C. 4x−2y−3 = 0
D. 4x+2y−5 = 0
-
Bài tập 1.76 trang 42 SBT Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x+y−2 = 0. Phép vị tự tâm O tỉ số k = −2 biến d thành đường thẳng có phương trình
A. 2x+2y = 0
B. 2x+2y−4 = 0
C. x+y+4 = 0
D. x+y−4 = 0
-
Bài tập 1.77 trang 42 SBT Hình học 11
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x−1)2+(y−2)2 = 4. Phép vị tự tâm O tỉ số k = −2 biến (C) thành đường tròn có phương trình
A. (x−2)2+(y−4)2 = 16
B. (x−4)2+(y−2)2 = 4
C. (x−4)2+(y−2)2 = 16
D. (x+2)2+(y+4)2 = 16
-
Bài tập 1.78 trang 42 SBT Hình học 11
Trong mặt phẳng Oxy cho điểm M(2;4). Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số \(k = \frac{1}{2}\) và phép đối xứng qua trục Oy sẽ biến điểm M thành điểm có tọa độ
A. (1;2) B. (−2;4)
C. (−1;2) D. (1;- 2)
-
Bài tập 1 trang 34 SGK Hình học 11 NC
Cho hai đường tròn (O ; R), (O’ ; R’) và một đường thẳng d
a. Tìm hai điểm M, N lần lượt nằm trên hai đường tròn đó sao cho d là đường trung trực của đoạn thẳng MN
b. Xác định điểm I trên d sao cho tiếp tuyến IT của (O ; R) và tiếp tuyến IT’ của (O’ ; R’) hợp thành các góc mà d là một trong các đường phân giác của các góc đó
-
Bài tập 2 trang 34 SGK Hình học 11 NC
Chứng minh rằng nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng
-
Bài tập 3 trang 34 SGK Hình học 11 NC
Cho đường thẳng d đi qua hai điểm phân biệt P, Q và hai điểm A, B nằm về một phía đối với d. Hãy xác định trên d hai điểm M, N sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \) và AM + BN bé nhất
-
Bài tập 4 trang 34 SGK Hình học 11 NC
Cho vecto \({\vec u}\) và điểm O. Với điểm M bất kì, ta gọi M1là điểm đối xứng với M qua O và M’ là điểm sao cho \(\overrightarrow {{M_1}M} = \vec u\). Gọi F là phép biến hình biến M thành M’
a. F là phép hợp thành của hai phép nào ? F có phải là phép dời hình hay không ?
b. Chứng tỏ rằng F là một phép đối xứng tâm
-
Bài tập 5 trang 34 SGK Hình học 11 NC
Cho tam giác ABC nội tiếp trong đường tròn (O) và một điểm M thay đổi trên (O). Gọi M1 là điểm đối xứng với M qua A, M2 là điểm đối xứng với M1 qua B, M3 là điểm đối xứng với M2 qua C
a. Chứng tỏ rằng phép biến hình F biến điểm M thành M3 là một phép đối xứng tâm
b. Tìm quỹ tích điểm M3
-
Bài tập 6 trang 34 SGK Hình học 11 NC
Gọi F là phép biến hình có tính chất sau đây: Với mọi cặp điểm M, N và ảnh M’, N’ của chúng, ta luôn có \(\overrightarrow {M'N'} = k\overrightarrow {MN} \) , trong đó k là một số không đổi khác 0. Hãy chứng minh rằng F là phép tịnh tiến hoặc phép vị tự
-
Bài tập 7 trang 34 SGK Hình học 11 NC
a. Cho tam giác ABC và hình vuông MNPQ như hình 27. Gọi V là phép vị tự tâm A tỉ số \(k = \frac{{AB}}{{AM}}\) . Hãy dựng ảnh của hình vuông MNPQ qua phép vị tự V
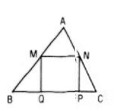
b. Từ bài toán ở câu a) hãy suy ra cách giải bài toán sau: Cho tamn giác nhọn ABC, hãy dựng hình vuông MNPQ sao cho hai đỉnh P, Q nằm trên cạnh BC và hai đỉnh M, N lần lượt nằm trên hai cạnh AB và AC
-
Bài tập 8 trang 35 SGK Hình học 11 NC
Cho đường tròn (O) có đường kính AB. Gọi C là điểm đối xứng với A và B và PQ là đường kính thay đổi của (O) khác đường kính AB. Đường thẳng CQ cắt PA và PB lần lượt tại M và N
a. Chứng minh rằng Q là trung điểm của CM, N là trung điểm của CQ.
b. Tìm quỹ tích các điểm M và N khi đường kính PQ thay đổi
-
Bài tập 9 trang 35 SGK Hình học 11 NC
Cho đường tròn (O ; R) và điểm A cố định Một dãy cung BC thay đổi của (O ; R) có độ dài không đổi BC = m. Tìm quỹ tích các điểm G sao cho \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
-
Bài tập 1 trang 35 SGK Hình học 11 NC
Cho hai đường thẳng song song d và d’. Có bao nhiêu phép tịnh tiến biến d thành d’
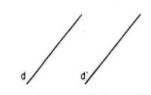
A. Không có phép tịnh tiến nào
B. Có duy nhất một phép tịnh tiến
C. Chỉ có hai phép tịnh tiến
D. Có vô số phép tịnh tiến
-
Bài tập 2 trang 35 SGK Hình học 11 NC
Cho bốn đường thẳng a, b , a’, b’ trong đó a // a’, b // b’, a cắt b. Có bao nhiêu phép tịnh tiến biến a và b thành a’ và b’ ?
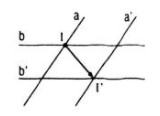
A. Không có phép tịnh tiến nào
B. Có duy nhất một phép tịnh tiến
C. Chỉ có hai phép tịnh tiến
D. Có rất nhiều phép tịnh tiến
-
Bài tập 3 trang 35 SGK Hình học 11 NC
Cho hai đường thẳng cắt nhau d và d’. Có bao nhiêu phép đối xứng trục biến d thành d’ ?
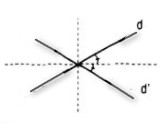
A. Không có phép đối xứng trục nào
B. Có duy nhất một phép đối xứng trục
C. Chỉ có hai phép đối xứng trục
D. Có rất nhiều phép đối xứng trục
-
Bài tập 4 trang 35 SGK Hình học 11 NC
Trong các hình dưới đây, hình nào có bốn trục đối xứng ?
A. Hình bình hành
B. Hình bình hành
C. Hình thoi
D. Hình vuông
-
Bài tập 5 trang 35 SGK Hình học 11 NC
Trong các mệnh đề sau, mệnh đề nào sai ?
A. Hình gồm hai đường tròn không bằng nhau có trục đối xứng
B. Hình gồm một đường tròn và một đoạn thẳng tùy ý có trục đối xứng
C. Hình gồm một đường tròn và một đường thẳng tùy ý có trục đối xứng
D. Hình gồm một tam cân và đường tròn ngoại tiếp tam giác đó có trục đối xứng
-
Bài tập 6 trang 35 SGK Hình học 11 NC
Trong các hình sau đây, hình nào không có tâm đối xứng ?
A. Hình gồm một đường tròn và một hình chữ nhật nội tiếp
B. Hình gồm một đường tròn và một tam giác đều nội tiếp
C. Hình lục giác đều
D. Hình gồm một hình vuông và đường tròn nội tiếp
-
Bài tập 7 trang 36 SGK Hình học 11 NC
Cho hình vuông ABCD tâm O. Xét phép quay Q có tâm quay O và góc quay φ. Với giá trị nào sau đây của φ, phép quay Q biến hình vuông ABCD thành chính nó ?
A. \(\varphi = \frac{\pi }{6}\)
B. \(\varphi = \frac{\pi }{4}\)
C. \(\varphi = \frac{\pi }{3}\)
D. \(\varphi = \frac{\pi }{2}\)
-
Bài tập 8 trang 36 SGK Hình học 11 NC
Cho hai đường thẳng song song d và d’. Có bao nhiêu phép vị tự với tỉ số k = 100 biến d thành d’ ?
A. Không có phép nào
B. Có duy nhất một phép
C. Chỉ có hai phép
D. Có rất nhiều phép
-
Bài tập 9 trang 36 SGK Hình học 11 NC
Cho đường tròn (O ; R). Tìm mệnh đề sai trong các mệnh đề sau đây:
A. Có phép tịnh tiến biến (O ; R) thành chính nó
B. Có hai phép vị tự biến (O ; R) thành chính nó
C. Có phép đối xứng trục biến (O ; R) thành chính nó
D. Trong ba mệnh đề A, B, C, có ít nhất một mệnh đề sai
-
Bài tập 10 trang 36 SGK Hình học 11 NC
Trong các mệnh đề sau đây, mệnh đề nào sai ?
A. Tâm vị tự ngoài của hai đường tròn nằm ngoài hai đường tròn đó
B. Tâm vị tự ngoài của hai đường tròn không nằm giữa hai tâm của hai đường tròn đó
C. Tâm vị tự trong của hai đường tròn luôn thuộc đoạn thẳng nối tâm hai đường tròn đó
D. Tâm vị tự của hai đường tròn có thể là điểm chung của cả hai đường tròn đó
-
Bài tập 11 trang 36 SGK Hình học 11 NC
Phép biến hình nào sau đây không có tính chất: “Biến một đường thẳng thành đường thẳng song song hoặc trùng với nó” ?
A. Phép tịnh tiến
B. Phép đối xứng tâm
C. Phép đối xứng trục
D. Phép vị tự
-
Bài tập 12 trang 36 SGK Hình học 11 NC
Trong các mệnh đề sau đây, mệnh đề nào sai ?
A. Phép dời hình là một phép đồng dạng
B. Phép vị tự là một phép đồng dạng
C. Phép đồng dạng là một phép dời hình
D. Có phép vị tự không phải là phép dời hình


