Bài tập 3 trang 34 SGK Hình học 11 NC

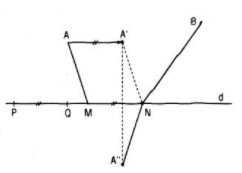
Giả sử hai điểm M, N nằm trên d sao cho \(\overrightarrow {MN}  = \overrightarrow {PQ} \)

Lấy điểm A’ sao cho \(\overrightarrow {AA'}  = \overrightarrow {PQ} \)  thì điểm A’ hoàn toàn xác định và AMNA’ là hình bình hành nên AM = A’N

Ta có: AM + BN = A’N + BN

Gọi A” là điểm đối xứng của A’ qua d, khi đó:

A’N + BN = A”N + BN ≥ A”B

Từ đó ta suy ra AM + BN nhỏ nhất khi N là giao điểm của BA” với d

Từ đó tìm được điểm M thỏa \(\overrightarrow {MN}  = \overrightarrow {AA'}  = \overrightarrow {PQ} \)

-- Mod Toán 11 HỌC247