Bài tập 6 trang 34 SGK Hình học 11 NC

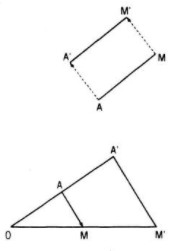
Ta lấy một điểm A cố định và đặt A’ = F(A)

Theo giả thiết, với điểm M bất kì và ảnh M’ =F(M) của nó, ta có \(\overrightarrow {A'M}  = k\overrightarrow {AM} \)

Nếu k = 1, thì \(\overrightarrow {A'M}  = \overrightarrow {AM} \), do đó \(\overrightarrow {MM'}  = \overrightarrow {AA'} \) ,và F là phép tịnh tiến theo vecto \(\overrightarrow {AA'} \)

Nếu k ≠ 1 thì có điểm O sao cho: \(\overrightarrow {OA'}  = k\overrightarrow {OA} \) (với O thỏa\(\overrightarrow {OA'}  = \frac{1}{{1 - k}}\overrightarrow {AA'} \))

Khi đó ta có:

\(\overrightarrow {OM'}  = \overrightarrow {OA'}  + \overrightarrow {A'M'} \)

\(= k\overrightarrow {OA}  + k\overrightarrow {AM}  = k\overrightarrow {OM} \)

Vậy F là phép vị tự tâm O, tỉ số k.

-- Mod Toán 11 HỌC247