Bài tập 8 trang 35 SGK Hình học 11 NC

Cho đường tròn (O) có đường kính AB. Gọi C là điểm đối xứng với A và B và PQ là đường kính thay đổi của (O) khác đường kính AB. Đường thẳng CQ cắt PA và PB lần lượt tại M và N

a. Chứng minh rằng Q là trung điểm của CM, N là trung điểm của CQ.

b. Tìm quỹ tích các điểm M và N khi đường kính PQ thay đổi

QUẢNG CÁO

Hướng dẫn giải chi tiết

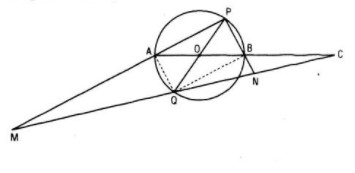
a) Ta có QB // AP (vì cùng vuông góc với PB) và B là trung điểm của AC nên Q là trung điểm của CM

Ta có AQ // BN (vì cùng vuông góc với AP) và B là trung điểm của AC nên N là trung điểm của CQ

b) Theo câu a) ta có \(\overrightarrow {CM} = 2\overrightarrow {CQ} \) nên phép vị tự V tâm C tỉ số biến Q thành M

Vì Q chạy trên đường tròn (O) (trừ hai điểm A, B) nên quỹ tích M là ảnh của đường tròn đó qua phép vị tự V (trừ ảnh của A, B)

Tương tự, ta có \(\overrightarrow {CN} = \frac{1}{2}\overrightarrow {CQ} \) nên quỹ tích N là ảnh của đường tròn (O) qua phép vị tự V tâm C, tỉ số 1/2 (trừ ảnh của A, B).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 8 trang 35 SGK Hình học 11 NC HAY thì click chia sẻ