Giải bài 1.33 tr 37 SBT Hình học 11
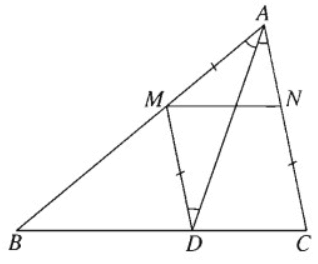
Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.
Hướng dẫn giải chi tiết
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó \(\widehat {MAD} = \widehat {MDA} = \widehat {DAC}\). Suy ra AD là phân giác trong của góc A. Do đó AD dựng được .Ta lại có \(\overrightarrow {NM} = \overrightarrow {CD} \), nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ \(\overrightarrow {DC} \).
Từ đó suy ra cách dựng:
- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.
- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ \(\overrightarrow {CD} \). d cắt AB tại M.
- Dựng N sao cho \(\overrightarrow {NM} = \overrightarrow {CD} \).
Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 1.31 trang 37 SBT Hình học 11
Bài tập 1.32 trang 37 SBT Hình học 11
Bài tập 1.34 trang 37 SBT Hình học 11
Bài tập 1.35 trang 37 SBT Hình học 10
Bài tập 1.36 trang 37 SBT Hình học 11
Bài tập 1.37 trang 37 SBT Hình học 11
Bài tập 1.38 trang 38 SBT Hình học 11
Bài tập 1.39 trang 38 SBT Hình học 11
Bài tập 1.40 trang 38 SBT Hình học 11
Bài tập 1.41 trang 38 SBT Hình học 11
Bài tập 1.42 trang 38 SBT Hình học 11
Bài tập 1.43 trang 38 SBT Hình học 11
Bài tập 1.44 trang 38 SBT Hình học 11
Bài tập 1.45 trang 38 SBT Hình học 11
Bài tập 1.46 trang 38 SBT Hình học 11
Bài tập 1.47 trang 38 SBT Hình học 11
Bài tập 1.48 trang 38 SBT Hình học 11
Bài tập 1.49 trang 39 SBT Hình học 11
Bài tập 1.50 trang 39 SBT Hình học 11
Bài tập 1.51 trang 39 SBT Hình học 11
Bài tập 1.52 trang 39 SBT Hình học 11
Bài tập 1.53 trang 39 SBT Hình học 11
Bài tập 1.54 trang 39 SBT Hình học 11
Bài tập 1.55 trang 39 SBT Hình học 11
Bài tập 1.56 trang 39 SBT Hình học 11
Bài tập 1.57 trang 39 SBT Hình học 11
Bài tập 1.58 trang 39 SBT Hình học 11
Bài tập 1.59 trang 40 SBT Hình học 11
Bài tập 1.60 trang 40 SBT Hình học 11
Bài tập 1.61 trang 40 SBT Hình học 11
Bài tập 1.62 trang 40 SBT Hình học 11
Bài tập 1.63 trang 40 SBT Hình học 11
Bài tập 1.64 trang 40 SBT Hình học 11
Bài tập 1.65 trang 40 SBT Hình học 11
Bài tập 1.66 trang 40 SBT Hình học 11
Bài tập 1.67 trang 41 SBT Hình học 11
Bài tập 1.68 trang 41 SBT Hình học 11
Bài tập 1.69 trang 41 SBT Hình học 11
Bài tập 1.70 trang 41 SBT Hình học 11
Bài tập 1.71 trang 41 SBT Hình học 11
Bài tập 1.72 trang 41 SBT Hình học 11
Bài tập 1.73 trang 41 SBT Hình học 11
Bài tập 1.74 trang 41 SBT Hình học 11
Bài tập 1.75 trang 42 SBT Hình học 11
Bài tập 1.76 trang 42 SBT Hình học 11
Bài tập 1.77 trang 42 SBT Hình học 11
Bài tập 1.78 trang 42 SBT Hình học 11
Bài tập 1 trang 34 SGK Hình học 11 NC
Bài tập 2 trang 34 SGK Hình học 11 NC
Bài tập 3 trang 34 SGK Hình học 11 NC
Bài tập 4 trang 34 SGK Hình học 11 NC
Bài tập 5 trang 34 SGK Hình học 11 NC
Bài tập 6 trang 34 SGK Hình học 11 NC
Bài tập 7 trang 34 SGK Hình học 11 NC
Bài tập 8 trang 35 SGK Hình học 11 NC
Bài tập 9 trang 35 SGK Hình học 11 NC
Bài tập 1 trang 35 SGK Hình học 11 NC
Bài tập 2 trang 35 SGK Hình học 11 NC
Bài tập 3 trang 35 SGK Hình học 11 NC
Bài tập 4 trang 35 SGK Hình học 11 NC
Bài tập 5 trang 35 SGK Hình học 11 NC
Bài tập 6 trang 35 SGK Hình học 11 NC
Bài tập 7 trang 36 SGK Hình học 11 NC
Bài tập 8 trang 36 SGK Hình học 11 NC
Bài tập 9 trang 36 SGK Hình học 11 NC
Bài tập 10 trang 36 SGK Hình học 11 NC
-


Cho phép quay \({Q_{\left( {O,\;\varphi } \right)}}\) biến điểm \(A\) thành điểm \(A'\) và biến điểm \(M\) thành điểm \(M'\). Mệnh đề nào sau đây là sai?
bởi Nguyễn Thủy Tiên
 25/02/2021
25/02/2021
A. \(\overrightarrow {AM} = \overrightarrow {A'M'} \)
B. \(\widehat {\left( {OA,{\rm{ }}OA'} \right)} = \widehat {\left( {OM,{\rm{ }}OM'} \right)} = \varphi \)
C. \(\widehat {\left( {\overrightarrow {AM} ,{\rm{ }}\overrightarrow {A'M'} } \right)} = \varphi \) với \(0 \le \varphi \le \pi \)
D. \(AM = A'M'\).
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng tọa độ \(Oxy\), tìm phương trình đường thẳng \(\Delta '\) là ảnh của đường thẳng \(\Delta :x + 2y - 1 = 0\) qua phép tịnh tiến theo véctơ \(\vec v = \left( {1; - 1} \right)\).
bởi Thúy Vân
 25/02/2021
25/02/2021
A. \(\Delta ':x + 2y - 3 = 0\).
B. \(\Delta ':x + 2y = 0\).
C. \(\Delta ':x + 2y + 1 = 0\).
D. \(\Delta ':x + 2y + 2 = 0\).
Theo dõi (0) 1 Trả lời -


Phép tịnh tiến theo \(\overrightarrow v = \left( {1;0} \right)\) biến điểm \(A\left( { - 2;3} \right)\) thành:
bởi Tra xanh
 25/02/2021
25/02/2021
A. \(A'\left( {3;0} \right)\)
B. \(A'\left( { - 3;0} \right)\)
C. \(A'\left( { - 1;3} \right)\)
D. \(A'\left( { - 1;6} \right)\)
Theo dõi (0) 1 Trả lời