Giải bài 3.4 tr 147 SBT Hình học 10
Lập phương trình ba đường trung trực của một tam giác có trung điểm các cạnh lần lượt là M(-1; 0), N(4; 1), P(2; 4).
Hướng dẫn giải chi tiết
Ta có: \({\overrightarrow n _{{\Delta _1}}} = \overrightarrow {NP} = \left( { - 2;3} \right)\)
Vậy Δ1 có phương trình: - 2(x + 1) + 3y = 0 ⇔ 2x - 3y + 2 = 0
Ta có: \({\overrightarrow n _{{\Delta _2}}} = \overrightarrow {MP} = \left( {3;4} \right)\)
Vậy Δ2 có phương trình: 3(x - 4) + 4(y - 1) = 0 ⇔ 3x + 4y - 16 = 0
Ta có: \({\overrightarrow n _{{\Delta _3}}} = \overrightarrow {MN} = \left( {5;1} \right)\)
Vậy Δ3 có phương trình: 5(x - 2) + (y - 4) = 0 ⇔ 5x + y - 14 = 0
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 3.2 trang 147 SBT Hình học 10
Bài tập 3.3 trang 147 SBT Hình học 10
Bài tập 3.5 trang 147 SBT Hình học 10
Bài tập 3.6 trang 147 SBT Hình học 10
Bài tập 3.7 trang 147 SBT Hình học 10
Bài tập 3.8 trang 147 SBT Hình học 10
Bài tập 3.9 trang 147 SBT Hình học 10
Bài tập 3.10 trang 148 SBT Hình học 10
Bài tập 3.11 trang 148 SBT Hình học 10
Bài tập 3.12 trang 148 SBT Hình học 10
Bài tập 3.13 trang 148 SBT Hình học 10
Bài tập 3.14 trang 148 SBT Hình học 10
Bài tập 1 trang 79 SBT Hình học 10
Bài tập 2 trang 79 SGK Hình học 10 NC
Bài tập 3 trang 80 SGK Hình học 10 NC
Bài tập 4 trang 80 SGK Hình học 10 NC
Bài tập 5 trang 80 SGK Hình học 10 NC
Bài tập 6 trang 80 SGK Hình học 10 NC
Bài tập 7 trang 73 SGK Hình học 10 NC
Bài tập 8 trang 84 SGK Hình học 10 NC
Bài tập 9 trang 84 SGK Hình học 10 NC
Bài tập 10 trang 84 SGK Hình học 10 NC
Bài tập 11 trang 84 SGK Hình học 10 NC
Bài tập 12 trang 84 SGK Hình học 10 NC
Bài tập 13 trang 85 SGK Hình học 10 NC
Bài tập 14 trang 85 SGK Hình học 10 NC
Bài tập 15 trang 89 SGK Hình học 10 NC
Bài tập 16 trang 90 SGK Hình học 10 NC
Bài tập 17 trang 90 SGK Hình học 10 NC
Bài tập 18 trang 90 SGK Hình học 10 NC
Bài tập 19 trang 90 SGK Hình học 10 NC
-
Lập phương trình đường thẳng (d) đi qua A(2;-3) và vuông góc với đường thẳng -4x +3y +5=0?
bởi anh vân
24/06/2020
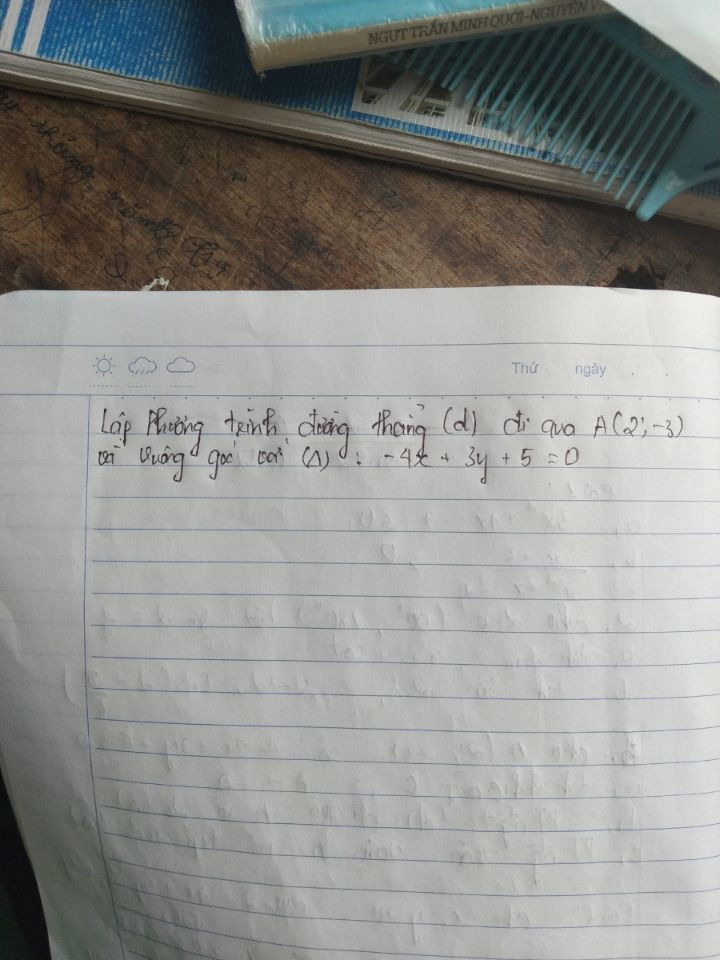Theo dõi (0) 3 Trả lời -
Tìm tọa độ điểm A thuộc đường thẳng \(\Delta \) sao cho A cách M một khoảng bằng \(\sqrt 13\)?
bởi Thanh Thúy
21/06/2020
Lời giải chi tiết ạ
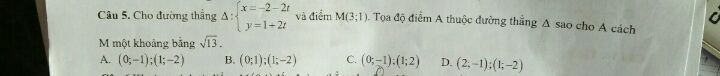Theo dõi (1) 3 Trả lời -
Viết PT đường thẳng qua C và cách điểm A một khoảnh bằng 3?
bởi Thanh Ngan Nguyen
19/06/2020
A(4; -2 ) B(- 3 ; 2) C(1;6) . Viết PT đường thẳng qua C và cách điểm A một khoảnh bằng 3
Theo dõi (0) 0 Trả lời -
Cho hai điểm A(1;2), B(3;4)
a, Viết phương trình tổng quát của đường thẳng qua A và vuông góc với AB
b, Viết phương trình đường tròn đường kính AB
Theo dõi (1) 2 Trả lời -
ADMICRO
Giải dùm e
Theo dõi (0) 2 Trả lời -
Viết phương trình đường thẳng chứa cạnh AB và đường cao kẻ từ A của tam giác ABC?
bởi Neko Loli Chan
13/06/2020
Giúp em với ạ!
Trong mp toạ độ Oxy, cho tam giác ABC có A(-2;-1), B(1;-2), C(-4;3) :
a) viết phương trình đường thẳng chứa cạnh AB và đường cao kẻ từ A của tam giác ABC.
b) viết phương trình đường tròn ngoại tiếp tam giác ABC.
c) viết phương trình đường thẳng đi qua d và cách đều hai điểm A và C
Theo dõi (0) 1 Trả lời -
Tìm toạ đồ đỉnh A?
bởi Nguyen Bich Hong
12/06/2020
Trong mặt phẳng với hệ toạ độ oxy, cho tam giác ABC có 2 đường cao BM,CN. Giả sử BC, BM, CN lần lượt có phương trình là -x 9y 6=0 ; 3x-y 8=0; x y-6=0. Toạ độ đỉnh A là ?
Theo dõi (0) 1 Trả lời -
Viết phương trình tổng quát của các đường thẳng của các đường thẳng chứa cạnh BC?
bởi Vũ Dương
12/06/2020
Trong mặt phẳng với hệ tọa độ Oxy, cho ∆ABC với A(2;1), B(4;3),C(6;7)
a) Viết phương trình tổng quát của các đường thẳng của các đường thẳng chứa cạnh BC
b) Viết phương trình đường tròn có tâm là trọng tâm G của ∆ABC và tiếp xúc với đường thẳng BC
Theo dõi (0) 1 Trả lời -
Tìm khoảng cách từ điểm O (0;0) tới đường thẳng \(\Delta :\frac{x}{6} + \frac{y}{8} = 1\)?
bởi Nguyễn Ly
12/06/2020
Câu 32
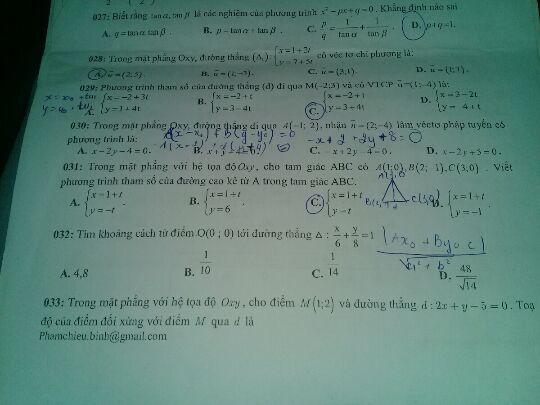Theo dõi (0) 1 Trả lời -
Đề kiểm tra học kì 2
Theo dõi (1) 3 Trả lời
