Bài tập 3 trang 80 SGK Hình học 10 NC

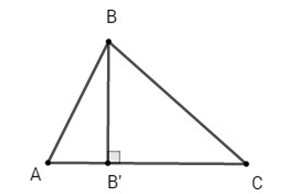
Hai đường thẳng AB, BC cắt nhau tại B nên tọa độ của B là nghiệm của hệ phương trình sau:

\(\left\{ \begin{array}{l}
2x - 3y - 1 = 0\\
x + 3y + 7 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x =  - 2\\
y =  - \frac{5}{3}
\end{array} \right.\)

Vậy \(B\left( { - 2; - \frac{5}{8}} \right)\)

Đường thẳng CA có véc tơ pháp tuyến \(\overrightarrow n  = \left( {5; - 2} \right)\) nên có véc tơ chỉ phương là \(\overrightarrow u  = \left( {2;5} \right)\)

Đường cao kẻ từ đỉnh B vuông góc với CA nên nhận véc tơ chỉ phương là \(\overrightarrow u  = \left( {2;5} \right)\) của CA làm véc tơ pháp tuyến.

Phương trình tổng quát của đường cao kẻ từ đỉnh B đi qua \(B\left( { - 2; - \frac{5}{8}} \right)\) và có véc tơ pháp tuyến \(\overrightarrow u  = \left( {2;5} \right)\) là:

\(\begin{array}{l}
2\left( {x + 2} \right) + 5\left( {x + \frac{5}{3}} \right) = 0\\
 \Leftrightarrow 2x + 5y + \frac{{37}}{3} = 0
\end{array}\)

-- Mod Toán 10 HỌC247