Giải bài 3.12 tr 148 SBT Hình học 10
Lập phương trình các đường phân giác của các góc giữa hai đường thẳng:
Δ1: 2x + 4y + 7 = 0 và Δ2: x - 2y - 3 = 0.
Hướng dẫn giải chi tiết
Phương trình hai đường phân giác của các góc giữa Δ1 và Δ2 là:
\(\begin{array}{l}
\frac{{2x + 4y + 7}}{{\sqrt {4 + 16} }} = \pm \frac{{x - 2y - 3}}{{\sqrt {1 + 4} }}\\
\Leftrightarrow \left[ \begin{array}{l}
2x + 4y + 7 = 2\left( {x - 2y - 3} \right)\\
2x + 4y + 7 = - 2\left( {x - 2y - 3} \right)
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
8y + 13 = 0\\
4x + 1 = 0
\end{array} \right.
\end{array}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 3.10 trang 148 SBT Hình học 10
Bài tập 3.11 trang 148 SBT Hình học 10
Bài tập 3.13 trang 148 SBT Hình học 10
Bài tập 3.14 trang 148 SBT Hình học 10
Bài tập 1 trang 79 SBT Hình học 10
Bài tập 2 trang 79 SGK Hình học 10 NC
Bài tập 3 trang 80 SGK Hình học 10 NC
Bài tập 4 trang 80 SGK Hình học 10 NC
Bài tập 5 trang 80 SGK Hình học 10 NC
Bài tập 6 trang 80 SGK Hình học 10 NC
Bài tập 7 trang 73 SGK Hình học 10 NC
Bài tập 8 trang 84 SGK Hình học 10 NC
Bài tập 9 trang 84 SGK Hình học 10 NC
Bài tập 10 trang 84 SGK Hình học 10 NC
Bài tập 11 trang 84 SGK Hình học 10 NC
Bài tập 12 trang 84 SGK Hình học 10 NC
Bài tập 13 trang 85 SGK Hình học 10 NC
Bài tập 14 trang 85 SGK Hình học 10 NC
Bài tập 15 trang 89 SGK Hình học 10 NC
Bài tập 16 trang 90 SGK Hình học 10 NC
Bài tập 17 trang 90 SGK Hình học 10 NC
Bài tập 18 trang 90 SGK Hình học 10 NC
Bài tập 19 trang 90 SGK Hình học 10 NC
-
Xét vị trí tương đối của các cặp đường thẳng d1 và d2 trong các trường hợp
bởi Hoàng Thùy Dung
14/04/2020
Làm hộ em bài 8;ý a ,e g ạ
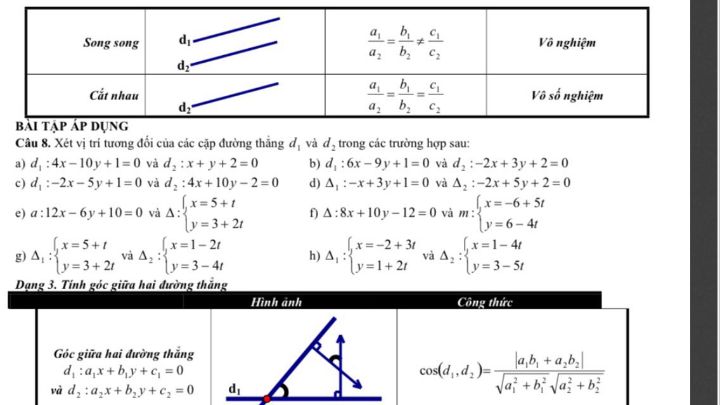Theo dõi (0) 1 Trả lời -
Lập phương trình tham số của đường thẳng d ?
bởi Vũ Thùy Trang
13/04/2020
Câu 1. Lập phương trình tham số của đường thẳng d biết d:
a) Đi qua
và có VTCP 
b) Đi qua 
và có VTCP 
c) Đi qua gốc tọa độ O và có VTCP
d) Đi qua 
và có VTCP 
e) Đi qua
và có VTPT 
f) Đi qua 
và có VTPT 
g) Cho
và điểm 
thỏa 
. Viết ptts đt đi qua và có VTCP 
.Theo dõi (0) 1 Trả lời -
Viết PTTQ các cạnh AB, BC, CA biết tam giác ABC có A(-2;1), trung tuyến BB’ có phương trình 2x-3y-1=0
bởi Trần Lê
13/04/2020
Cho tam giác ABC biết A(-2;1), trung tuyến BB’ có phương trình : 2x-3y-1=0, trung tuyến CC’ có phương trình x+y-2=0. Viết PTTQ các cạnh AB, BC, CA.
Theo dõi (0) 1 Trả lời -
Viết phương trình đường thẳng đi qua A(-1;2) và cách B(1;2) một khoảng lớn nhất
bởi Đoàn Thị Trà
12/04/2020
Viết phương trình đường thẳng đi qua A(-1;2) và cách B(1;2) một Khoảng lớn nhấtTheo dõi (0) 0 Trả lời -
ADMICRO
Lập PTTS, PTCT, PTTQ của các đường thẳng:
bởi Minh Hiếu
12/04/2020
Theo dõi (1) 0 Trả lời -
Xác định tọa độ diểm E để tứ giác ABCE là hình bình hành biết A(3;3), B(9;3), C(6;-3)
bởi Nhi Phan
11/04/2020
Trong mặt phẳng tọa độ Oxy cho tam giác ABC có A(3;3), B(9;3), C(6;-3)
a/ Xác định tọa độ diểm E để tứ giác ABCE là hình bình hành
b/ Tìm điểm D trên trục sao cho ABD thẳng hàng
c/ Tính chu vi (P) của tam giác ABC
d/ Tìm M trên đường thẳng
: y= -2x+6 sao cho MA2 + MB2 + MC2 đạt giá trị nhỏ nhất.
Theo dõi (1) 0 Trả lời -
Tìm điểm M trên đường thẳng d sao cho tổng các khoảng cách từ M đến AB là nhỏ nhất biết A(0;2);B(2;-2)
bởi Nguyễn Bắc
11/04/2020
Giúp em với ạ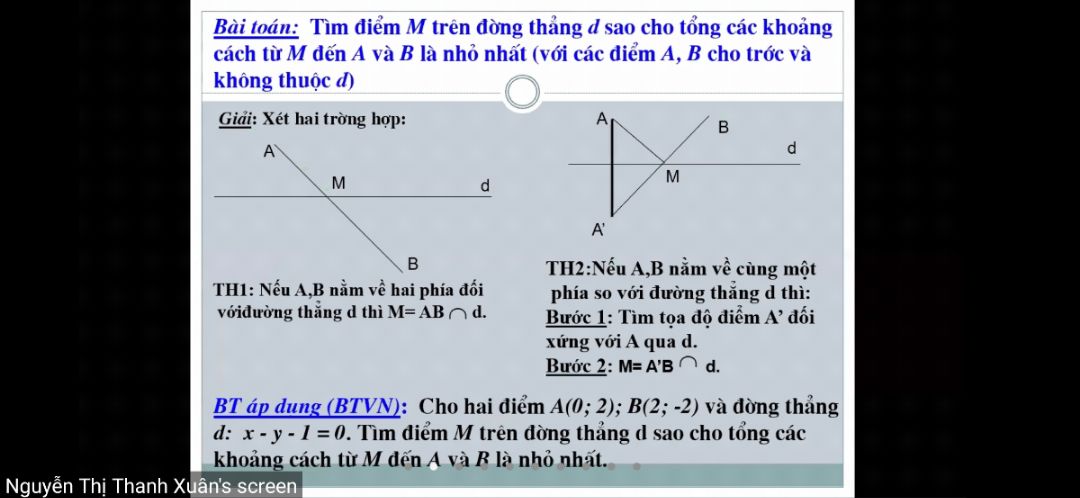
Theo dõi (1) 0 Trả lời -
Tìm tọa độ điểm M?
bởi Băng Nguyễn Thái Lạc
10/04/2020
Bài 31 ấy ạ
Theo dõi (0) 0 Trả lời -
Đường thẳng đi qua A(1; -2) có VTPT \(\overrightarrow n = \left( { - 1;2} \right)\) có phương trình tổng quát là?
bởi Bảo Thanh
10/04/2020
Giải
Theo dõi (0) 1 Trả lời -
Viết phương trình các cạnh của tam giác ABC?
bởi Van Anh Nguyen
10/04/2020
Theo dõi (0) 0 Trả lời
