Giải bài 3.6 tr 147 SBT Hình học 10
Cho tam giác ABC, biết phương trình đường thẳng AB: x - 3y + 11 = 0, đường cao AH: 3x + 7y - 15 = 0, đường cao BH: 3x - 5y + 13 = 0. Tìm phương trình hai đường thẳng chứa hai cạnh còn lại của tam giác.
Hướng dẫn giải chi tiết
Theo đề bài tọa độ điểm A luôn thỏa mãn hệ phương trình:
\(\left\{ \begin{array}{l}
x - 3y = - 11\\
3x + 7y = 15
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = - 2\\
y = 3
\end{array} \right.\)
Vì AC ⊥ BH nên C có dạng: 5x + 3y + c = 0, ta có:
A ∈ AC ⇔ -10 + 9 + c = 0 ⇔ c = 1
Vậy phương trình đường thẳng chứa cạnh AC: 5x + 3y + 1 = 0.
Tọa độ của điểm B luôn thỏa mãn hệ phương trình:
\(\left\{ \begin{array}{l}
x - 3y = - 11\\
3x - 5y = - 13
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 4\\
y = 5
\end{array} \right.\)
Vì BC ⊥ AH nên BC có dạng: 7x - 3y + c = 0, ta có:
B ∈ BC ⇔ 28 - 15 + c = 0 ⇔ c = -13
Vậy phương trình đường thẳng chứa cạnh BC: 7x - 3y - 13 = 0.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 3.4 trang 147 SBT Hình học 10
Bài tập 3.5 trang 147 SBT Hình học 10
Bài tập 3.7 trang 147 SBT Hình học 10
Bài tập 3.8 trang 147 SBT Hình học 10
Bài tập 3.9 trang 147 SBT Hình học 10
Bài tập 3.10 trang 148 SBT Hình học 10
Bài tập 3.11 trang 148 SBT Hình học 10
Bài tập 3.12 trang 148 SBT Hình học 10
Bài tập 3.13 trang 148 SBT Hình học 10
Bài tập 3.14 trang 148 SBT Hình học 10
Bài tập 1 trang 79 SBT Hình học 10
Bài tập 2 trang 79 SGK Hình học 10 NC
Bài tập 3 trang 80 SGK Hình học 10 NC
Bài tập 4 trang 80 SGK Hình học 10 NC
Bài tập 5 trang 80 SGK Hình học 10 NC
Bài tập 6 trang 80 SGK Hình học 10 NC
Bài tập 7 trang 73 SGK Hình học 10 NC
Bài tập 8 trang 84 SGK Hình học 10 NC
Bài tập 9 trang 84 SGK Hình học 10 NC
Bài tập 10 trang 84 SGK Hình học 10 NC
Bài tập 11 trang 84 SGK Hình học 10 NC
Bài tập 12 trang 84 SGK Hình học 10 NC
Bài tập 13 trang 85 SGK Hình học 10 NC
Bài tập 14 trang 85 SGK Hình học 10 NC
Bài tập 15 trang 89 SGK Hình học 10 NC
Bài tập 16 trang 90 SGK Hình học 10 NC
Bài tập 17 trang 90 SGK Hình học 10 NC
Bài tập 18 trang 90 SGK Hình học 10 NC
Bài tập 19 trang 90 SGK Hình học 10 NC
-


Hệ số góc k của phương trình tổng quát là gì?
bởi Ngọc Linh
 06/06/2020
06/06/2020
Hệ số góc k của phương trình tổng quát là gì?
Theo dõi (0) 4 Trả lời -


Tìm tọa độ điểm D?
bởi Đỗ Thị Hạnh Ngân
 06/06/2020
06/06/2020
Viết phương trình đường thẳng
Trong hệ tọa độ Oxy, cho hình thang vuông ABCD vuông tại A và B , đáy lớn AD. Biết chu vi hình thang là 16 4√216 42, diện tích hình thang là 24. Biết A(1;2),B(1;6)A(1;2),B(1;6). Tìm tọa độ đỉnh D biết hoành độ điểm Đ lớn hơn 2.
Theo dõi (0) 1 Trả lời -


Giúp mình với ạ
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình tổng quát của đường thẳng B trong mặt phẳng Oxy, cho A(1;1), B(2;-1), C(4;0).
bởi MiLu Tran
 03/06/2020
IkkjhhujvhyjjvvvTheo dõi (0) 0 Trả lời
03/06/2020
IkkjhhujvhyjjvvvTheo dõi (0) 0 Trả lời -
ADMICRO


Tính diện tích tam giác ABC?
bởi Vũ Hạnh
 03/06/2020
03/06/2020
Giải hộ từ câu d
Cho tam giác abc có A(-1,-2) B(2,2) C(5,0)
a) viết PTTS AC b) viết PTTQ đường cao BH
c) viết PTTQ của đường thẳng d đi qua C và // BH
d) tính diện tích tam giác ABC
e) tính góc tạo bởi đường thẳng AC và trục Ox
g) xác định tâm đường tròn ngoại tiếp tam giác ABC
Theo dõi (1) 1 Trả lời -


Giải hộ mình với
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để ∆ vuông góc ∆' ∆:2x y-4=0?
bởi .
 28/05/2020
Tìm m để ∆ vuông góc ∆' ∆:2x y-4=0Theo dõi (0) 0 Trả lời
28/05/2020
Tìm m để ∆ vuông góc ∆' ∆:2x y-4=0Theo dõi (0) 0 Trả lời -

 Theo dõi (1) 5 Trả lời
Theo dõi (1) 5 Trả lời -


Tìm m để \(\Delta \bot \Delta '\)?
bởi Thanh Thư Ngọc Trần
 27/05/2020
27/05/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Câu 161
Câu 161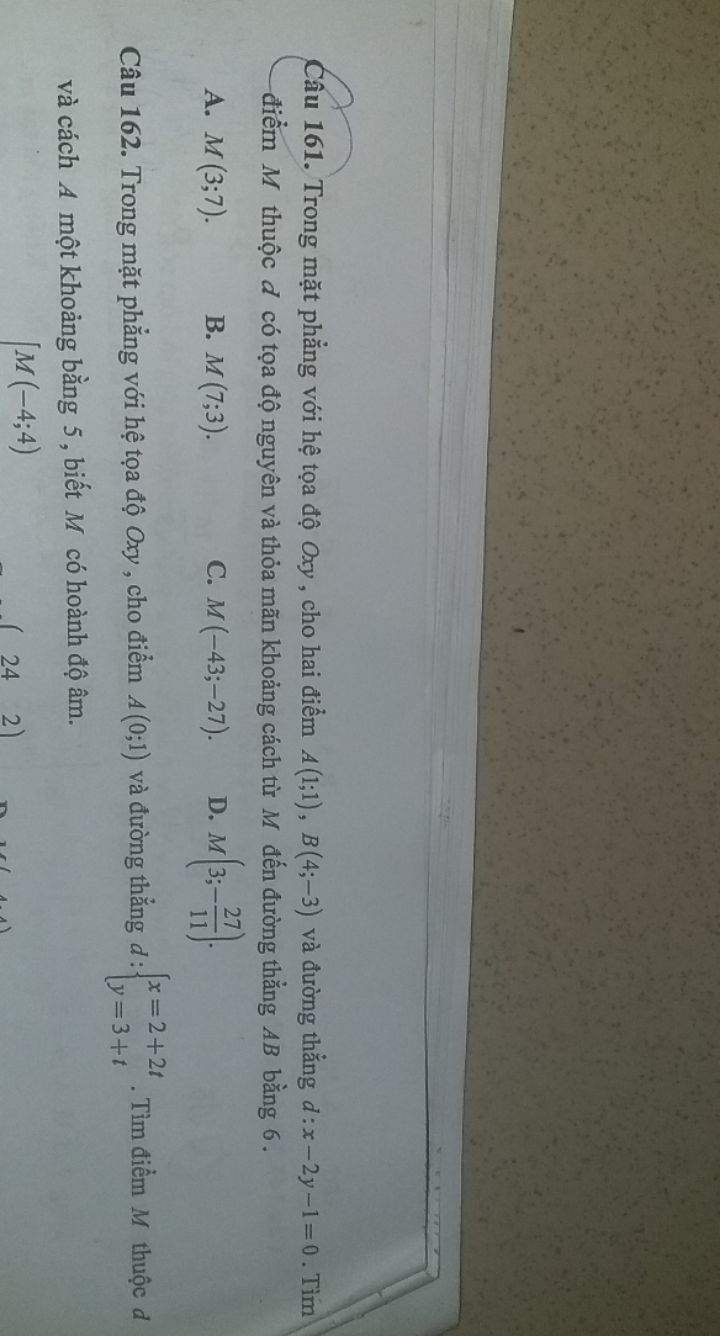 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời



