Giải bài 2.15 tr 91 SBT Hình học 10
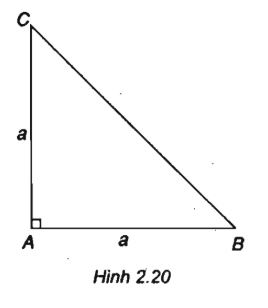
Tam giác ABC vuông tại A và có AB = AC = a. Tính:
a) \(\overrightarrow {AB} .\overrightarrow {AC} \)
b) \(\overrightarrow {BA} .\overrightarrow {BC} \)
c) \(\overrightarrow {AB} .\overrightarrow {BC} \)
Hướng dẫn giải chi tiết
\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC} = 0\\
\overrightarrow {BA} .\overrightarrow {BC} = a.a\sqrt 2 .\cos {45^0} = {a^2}\\
\overrightarrow {AB} .\overrightarrow {BC} a.a\sqrt 2 .\cos {135^0} = - {a^2}
\end{array}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 2.13 trang 91 SBT Hình học 10
Bài tập 2.14 trang 91 SBT Hình học 10
Bài tập 2.16 trang 91 SBT Hình học 10
Bài tập 2.17 trang 91 SBT Hình học 10
Bài tập 2.18 trang 92 SBT Hình học 10
Bài tập 2.19 trang 92 SBT Hình học 10
Bài tập 2.20 trang 92 SBT Hình học 10
Bài tập 2.21 trang 92 SBT Hình học 10
Bài tập 2.22 trang 92 SBT Hình học 10
Bài tập 2.23 trang 92 SBT Hình học 10
Bài tập 2.24 trang 92 SBT Hình học 10
Bài tập 2.25 trang 92 SBT Hình học 10
Bài tập 2.26 trang 92 SBT Hình học 10
Bài tập 2.27 trang 92 SBT Hình học 10
Bài tập 2.28 trang 92 SBT Hình học 10
Bài tập 4 trang 51 SGK Hình học 10 NC
Bài tập 5 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 7 trang 52 SGK Hình học 10 NC
Bài tập 8 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 11 trang 52 SGK Hình học 10 NC
Bài tập 12 trang 52 SGK Hình học 10 NC
-
Tam giác \(MNP\) có \(MN=4, MP=8,\) \(\widehat M = {60^0}\).Lấy điểm \(E\) trên tia \(MP\) và đặt \(\overrightarrow {ME} = k\overrightarrow {MP} \). Tìm \(k\) để \(NE\) vuông góc với trung tuyến \(MF\) của tam giác \(MNP.\)
bởi Thành Tính
23/02/2021
Theo dõi (0) 1 Trả lời -
Cho tam giác \(ABC\) có \(AB=7, AC=5,\) \(\widehat A = {120^0}\). Tính độ dài trung tuyến \(AM\) của tam giác (\(M\) là trung điểm của \(BC\) ).
bởi Dell dell
22/02/2021
Theo dõi (0) 1 Trả lời -
Cho tam giác \(ABC\) có \(AB=7, AC=5,\) \(\widehat A = {120^0}\). Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \) và \(\overrightarrow {AB} .\overrightarrow {BC} \).
bởi Lê Nhật Minh
23/02/2021
Theo dõi (0) 1 Trả lời -
Cho tam giác đều abc gọi d là điểm thỏa mãn vécto dc=2vectobd gọi R và r lần lược là bán kính đường tròn ngoại tiếp và nội tiếp tam giác adc tính tỉ số R/r
bởi Cường Tăng
22/02/2021
cho tam giác đều abc gọi d là điểm thỏa mãn vécto dc=2vectobd gọi R và r lần lược là bán kính đường tròn ngoại tiếp và nội tiếp tam giác adc tính tỉ số R/rTheo dõi (0) 0 Trả lời
