Bài tập 7 trang 52 SGK Hình học 10 NC
Cho bốn điểm bất kì A, B, C, D. Chứng minh rằng
\(\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0 \).
Từ đó suy ra một cách chứng minh định lí: “Ba đường cao của một tam giác đồng quy”.
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{*{20}{l}}
{\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} }\\
\begin{array}{l}
= \overrightarrow {DA} \left( {\overrightarrow {DC} - \overrightarrow {DB} } \right) + \overrightarrow {DB} \left( {\overrightarrow {DA} - \overrightarrow {DC} } \right)\\
+ \overrightarrow {DC} \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)
\end{array}\\
\begin{array}{l}
= \overrightarrow {DA} .\overrightarrow {DC} - \overrightarrow {DA} .\overrightarrow {DB} + \overrightarrow {DB} .\overrightarrow {DA} \\
- \overrightarrow {DB} .\overrightarrow {DC} + \overrightarrow {DC} .\overrightarrow {DB} - \overrightarrow {DC} .\overrightarrow {DA} = 0
\end{array}
\end{array}\)
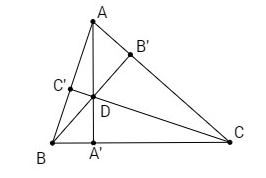
Gọi D là giao điểm của hai đường cao AA′, BB' của tam giác ABC.
Ta có \(\overrightarrow {DA} .\overrightarrow {BC} = 0,\overrightarrow {DB} .\overrightarrow {CA} = 0\)
Từ đó suy ra \(\overrightarrow {DA} .\overrightarrow {BC} = 0,\overrightarrow {DB} .\overrightarrow {CA} = 0\), do đó DC ⊥ AB.
Vậy D nằm trên đường cao CC′ của tam giác ABC, tức là ba đường cao trong tam giác đồng quy.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 5 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 8 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 11 trang 52 SGK Hình học 10 NC
Bài tập 12 trang 52 SGK Hình học 10 NC
-


Tính vecto AM.vecto AN biết M là trung điểm của BC
bởi Nguyễn Thủy
 06/11/2018
06/11/2018
cho hình vuông ABCD có cạnh bằng a. Gọi M là trung điểm của BC và N là điiểm nằm trên CD sao cho NC=2ND. tính vectoAM nhân vecto AN
Theo dõi (0) 1 Trả lời -


Tìm số đo các góc của tam giác ABC, biết rằng A(5;0), B(0;1), C(3;3)
Theo dõi (0) 2 Trả lời -


Tính cos(vt AB, vt BC)+sin( vt BA, vt BC)
bởi bach dang
 10/10/2018
10/10/2018
cho tam giác ABC vuông tại A và B = 30o .Tính các giá trị của biểu thức sau:
a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)
B) \(\sin\left(\overrightarrow{AB},\overrightarrow{AC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{BA}\right)+\cos\overrightarrow{CA},\overrightarrow{BA}\)
Theo dõi (0) 1 Trả lời -


Tính tổng (vt AB, vt BC)+(vt BC, vt CA)+(vt CA+vt AB)
bởi Thùy Nguyễn
 10/10/2018
10/10/2018
cho \(\Delta ABC\). Tổng \(\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\left(\overrightarrow{BC},\overrightarrow{CA}\right)+\left(\overrightarrow{CA},\overrightarrow{AB}\right)\) có thể chấp nhận giá trị nào trong các giá trị sau : \(90^o;180^o;270^o;360^o\) ?
Theo dõi (0) 1 Trả lời





