Giải bài 2.27 tr 92 SBT Hình học 10
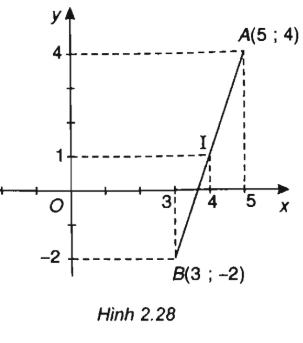
Trong mặt phẳng Oxy cho hai điểm A(5;4) và B(3;-2). Một điểm M di động trên trục hoành Ox. Tìm giá trị nhỏ nhất của \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\).
Hướng dẫn giải chi tiết
Gọi I là trung điểm của đoạn AB, ta có I(4; 1)
Vì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) nên \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2\left| {\overrightarrow {MI} } \right|\) nhỏ nhất khi giá trị của đoạn IM nhỏ nhất. Điểm M chạy trên trục Ox nên có tọa độ dạng M(x; 0). Do đó:
\(\left| {\overrightarrow {IM} } \right| = \sqrt {{{\left( {x - 4} \right)}^2} + 1} \ge 1\)Vậy giá trị nhỏ nhất của \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) là 2 khi M có tọa độ là M(4; 0).
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 2.25 trang 92 SBT Hình học 10
Bài tập 2.26 trang 92 SBT Hình học 10
Bài tập 2.28 trang 92 SBT Hình học 10
Bài tập 4 trang 51 SGK Hình học 10 NC
Bài tập 5 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 7 trang 52 SGK Hình học 10 NC
Bài tập 8 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 11 trang 52 SGK Hình học 10 NC
Bài tập 12 trang 52 SGK Hình học 10 NC
-
Tìm k để AM vuông góc với PN biết vt BM=kMC
bởi Lê Thị Tùng
22/12/2019
Theo dõi (0) 0 Trả lời -
Tính góc A của tam giác ABC biết A(3;1), B(-1;-1)
bởi manh
22/12/2019
Theo dõi (0) 0 Trả lời -
Tìm tọa đô trực tâm của tam giác ABC biết tam giác ABC có A(5; 3), B(2;-1), C (-1 ; 5)
bởi manh
22/12/2019
Cho tam giác ABC có A ( 5; 3) B (2;-1 ) C (-1 ; 5) . Tìm tọa đô trực tâm của tam giác ABCTheo dõi (1) 10 Trả lời -
Tìm toạ độ I là tâm đường tròn ngoại tiếp tam giác ABD
bởi Khanh Linh
22/12/2019
Trong mp toạ độ Oxy cho A(3;6) B(-5;2) D(1;-4) a) Tìm toạ độ C thuộc Ox sao cho tam giác ABC vuông tại A. Tính S tam giác ABC b) Tìm toạ độ I là tâm đường tròn ngoại tiếp tam giác ABDTheo dõi (0) 0 Trả lời
