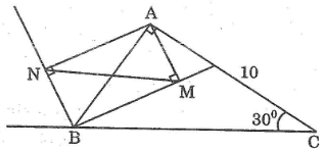
Bài tập 97 trang 122 SBT Toán 9 Tập 1

Bài 1:Cho tam giác ABC vuông tại A,đường cao AH,biết AB/AC=3/4;AH=4,8.Tính các cạnh của tam giác ABC

Cho x,y, z ≥ 0 thỏa mãn x=y +z=1

CMR: 4(1-x)(1-y)(1-z) ≤ x+2y+z

Mọi giúp em bài hình này nha. Không cần hình cũng được vì em đã vẽ được rồi ạ. Mong anh chị thầy cô giúp đỡ.

Cho đường tròn tâm O bán kính 2R, lấy điểm I nằm ngoài đường tròn. Từ I kẻ hai tiếp tuyến lần lược là IA và IB. OI cắt AB tại điểm H. Lấy điểm F đối xứng với H qua O. Từ F kẻ một đường thẳng cắt IA và IB lần lược tại các điểm G,E.

a) Cmr: OAIB và GAHF là tứ giác nội tiếp.

b) Tính độ dài cạnh OI khi OH= R. ( Tính theo R)

c) Chứng minh đẳng thức sau:

• GI.EF = GF.EI

• FA+AI-BF = IG-EB

d) Chứng minh rằng tứ giác GABE là hình thang cân. Đồng thời chứng minh đẳng thức sau:

180-2FOA+2AFI=0

Đây là bài thi thử của tỉnh Bình Dương năm 2017-2018. Em năm nay thi tuyển sinh mong mọi người giúp đỡ.

Cho tam giác ABC biết BC=7,5 AC=4,5 AB =6

a)tính AH

b)Tính BH,CH

Cho các số thực x,y,z thỏa mãn \(\left\{{}\begin{matrix}xyz=8\\xy+yz+xz< 2\left(x+y+z\right)\end{matrix}\right.\)

Chứng minh trong 3 số x,y,z có đúng một số lớn hơn 2

trên bảng có hai sô 1vaf 5 ta ghi các số tiếp theo lên bảng theo quy tắc: nếu có hai số x,y phân biệt trên bảng thì ghi thêm số z=x+y+xy. Chứng minh rằng tất cả các sô trên bảng trừ số 1 đều có dạng 3k+2

Cho tam giác ABC nhọn, \(S=1\). Vẽ 3 đường cao AD, BE, CF. C/m:

a) \(S_{AEF}+S_{BFD}+S_{CDE}=cos^2A+cos^2B+cos^2C\)

b)\(S_{DEF}=sin^2A-cos^2B-cos^2C\)

( Gợi ý: a) C/m: \(\dfrac{S_{AEF}}{S_{ABC}}=cos^2A\)

Help me phần b ,

a, CMR : \(\dfrac{a^2}{x}\) + \(\dfrac{b^2}{y}\)\(\ge\)\(\dfrac{\left(a+b\right)^2}{x+y}\)

b, CMR : \(\dfrac{1}{a^2+2bc}\)+ \(\dfrac{1}{b^2+2ac}\) + \(\dfrac{1}{c^2+2bc}\)\(\ge\) 9

1) Cho 3 số thực a,b,c thỏa mãn điều kiện: a+b+c+ab+bc+ca=6
CMR: a²+b²+c² >=3
2) Cho x,y là các số dương thỏa mãn x+y<=1
Tìm GTNN của \(P=\dfrac{1}{2\left(x^2+y^2\right)}+\dfrac{4}{xy}+2xy\)

Cho tam giác abc có ba góc nhọn nội tiếp trong đường tròn tâm O có bán kính bằng 3 cm các tiếp tuyến với O tại B và C cắt nhau tại C

A) Cm tứ giác OBDC nội tiếp đường tròn

B) Gọi M là giao điểm của BC và AD biết AB bằng 5 cm Tính diện tích của tam giác BCD

C) KẺ đường thẳng d đi qua D và song song với đường tiếp tuyến với (O) tại A, d cắt đường thẳng AB AC lần lượt tại P , Q Chứng minh AB.AP=AQ.AC

D) Cm góc PAD = góc MAC

Cho nủa đường tròn tâm O, đường kính AB Gọi C là một điểm ất kì trên nửa đường tròn đó và M là điểm chính giữa cung AC. Dây AC cắt dây BM tại H, đường thẳng AM cắt đường thẳng BC tại E.

a. Chứng minh EH vuông góc với AB

b. Chứng minh △ABE cân