Giải bài 39 tr 95 sách SGK Toán lớp 9 Tập 1
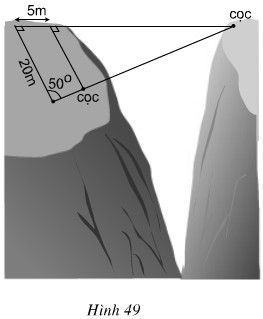
Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Áp dụng tính chất hai đường thẳng song song.
+) Dựa vào tỉ số lượng giác của góc nhọn.
Lời giải chi tiết
Giả sử hai cọc được đặt ở 2 điểm \(B\) và \(N\) trong hình vẽ.
Ta có: \(MN// AC\) (vì cùng vuông với \(AB\)) \( \Rightarrow \widehat{BNM}=\widehat{BCA}=50^0\) (hai góc đồng vị).
Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(\tan C = \dfrac{{AB}}{{AC}} \Rightarrow AB = AC.\tan50^o = 20.\tan50^o.\)
\(\Rightarrow BM=AB-AM=20\tan50^o - 5 \approx 18,835 \,m.\)
Xét tam giác \(BMN\) vuông tại \(M\) ta có: \(\sin \widehat {BNM}=\dfrac {BM}{BN}\)\(\Rightarrow BN = \dfrac{{BM}}{{\sin 50^o}} = \dfrac{{18,835}}{{\sin 50^o}} \approx 24,59\;m.\)
Vậy khoảng cách giữa hai cọc là: \(BN \approx 24,59\;m.\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Cho đường tròn (O,R). Từ điểm A nằm ngoài (O) kẻ hai tiếp tuyến AB , AC với (O) ( B, C là 2 tiếp điểm )
a, Gọi D là giao điểm của đoạn thẳng OA với (O) . Kẻ dây BE của (O) song song với OD, kẻ bán kính OF vuông góc với CD . Chứng minh C,O,E thẳng hàng và EF là tia phân giác góc CED
b, Vẽ đường tròn (A, AD). Gọi I,J lần lượt là giao điểm của đường thẳng ED và FD với đường tròn (A) ( I,J khác D). Chứng minh góc CEF = góc JID
c, Tính độ dài đoạn thẳng OA theo R để tứ giác EFIJ là hình bình hành
Theo dõi (0) 1 Trả lời -


Chứng minh A,B,O,C cùng thuộc một đường tròn. Xác định tâm và bán kính của đường tròn đó
bởi thu thủy
 22/02/2019
22/02/2019
Cho (O;R), dayy BC khác đường kính. Hai tiếp tuyến với (O) tại B,C cắt nhau tại A. Kẻ đường kính CD,BH vuông góc CD tại H.
a) CMR: A,B,O,C cùng thuộc một đường tròn. Xác định tâm và bán kính của đường tròn đó
b) CMR: AO vuông góc BC. Biết R=15 cm, BC=24 cm. Tính AB, OA
c) CMR: BC là tia phân giác của góc ABH
Theo dõi (0) 1 Trả lời -


Chứng minh rằng D,E,F,M cùng thuộc đường tròn
bởi Nguyễn Thanh Hà
 22/02/2019
22/02/2019
cho tam giac ABC nhọn Các đường cao AD,BE,CF cắt nhau tại H. Gọi M là trung điểm BC. chứng minh rằng D,E,F,M cùng thuộc đường tròn.
Theo dõi (0) 1 Trả lời -


Cho đoạn thẳng AB cố định, M di động trên AB. Trên cùng nửa mặt phẳng bờ AB vẽ hai hình vuông MADE và MBHG. Hai đường tròn ngoại tiếp hai hình vuông cắt nhau ở N.CMR: MN luôn đi qua một điểm cố định khi M di chuyển trên AB
Help me!!!!!!!!!!!!!!
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh AJ. BI ≤ AB^2/4
bởi Lê Nguyễn Hạ Anh
 22/02/2019
22/02/2019
cho tam giác đều ABC . trên BC, CA,AB lấy 3 điểm bất kì I,J,K sao cho K khác A,B và \(\widehat{\text{IJ}K}\)= 60. chứng minh AJ. BI\(\le\)\(\frac{AB^2}{4}\)
Theo dõi (0) 1 Trả lời -


Chứng minh diện tích hình tròn ngoại tiếp hình vuông bằng hai lần diện tích hình tròn nội tiếp hình vuông đó
bởi Nguyễn Thanh Hà
 22/02/2019
22/02/2019
Ai làm được bài này không giúp tớ với :
1. Chứng minh rằng diện tích hình tròn ngoại tiếp hình vuông bằng hai lần diện tích hình tròn nội tiếp hình vuông đó
Theo dõi (0) 1 Trả lời -


Chứng minh KF^2 = KE . KH
bởi Mai Vàng
 22/02/2019
22/02/2019
từ điểm M ở ngoài đường tròn (I) kẻ 2 tiép tuyến ME và MF ( E,F là 2 tiếp điểm ) kẻ dây EG của đường tròn (i) song song MF . Gọi H là giao điểm của MG với (I) và K là giao điểm của EH với MF
a) chứng Minh KF bình Phương = KE . KH
b) chứng Minh K là trung điểm MF
Theo dõi (0) 1 Trả lời -


Chứng minh 3 điểm A(1;-1), B(2; 1) và C(4;5) thẳng hàng
bởi hành thư
 22/02/2019
22/02/2019
Chứng minh 3 điểm A(1;-1), B(2; 1) và C(4;5) thẳng hàng.
Theo dõi (0) 1 Trả lời -


Chứng minh rằng AB.AC=2R.AH
bởi Nguyễn Thị Trang
 22/02/2019
22/02/2019
Cho tam giác ABC nội tiếp đường tròn (O;R) đường cao AH.
Chứng minh rằng:
a. AB.AC=2R.AH
b. S = \(\frac{abc}{4R}\) với BC = a, AC = b. S=S\(abc\).
Theo dõi (0) 1 Trả lời -


Bài 1 trang 102 sách bài tập toán 9 tập 1
bởi Thanh Truc
 08/10/2018
Bài 1 (Sách bài tập trang 102)
08/10/2018
Bài 1 (Sách bài tập trang 102)Hãy tính x và y trong các hình sau :
Theo dõi (0) 1 Trả lời -


Chứng minh AC là đường phân giác của góc BAE
bởi Lê Tường Vy
 22/02/2019
22/02/2019
Cho đường tròn đường kính AB. Qua C thuộc nửa đường tròn kẻ tiếp tuyến d với đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ A,B đến d và H là chân đường vuông góc kẻ từ C đến AB. CMR:
a) AC là đường phân giác của góc BAE
b) \(CH^2=BF.AE\)Theo dõi (0) 1 Trả lời





