Giải bài 34 tr 93 sách SGK Toán lớp 9 Tập 1
Chọn kết quả đúng trong các kết quả dưới đây:
a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?
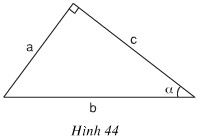
(A) \(\sin \alpha = {b \over c}\)
(B) \({\mathop{\rm cotg}\nolimits} \alpha = {b \over c}\)
(C) \(tg\alpha = {a \over c}\)
(D) \({\mathop{\rm cotg}\nolimits} \alpha = {a \over c}\)
b) Trong hình 45, hệ thức nào trong các hệ thức sau không đúng?
(A) sin2α + cos2 α = 1;
(B) sin α = cos β;
(C) cos β = sin(90°- α);
(D) \(tg\alpha = {{\sin \alpha } \over {\cos \alpha }}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Dựa vào các tỉ số lượng giác của góc nhọn để làm bài.
\(\sin \alpha = \dfrac{cạnh \, \, đối}{cạnh \, \, huyền}\) và \(\cos \alpha = \dfrac{cạnh \, \, kề}{cạnh \, \, huyền}.\)
\(\tan \alpha = \dfrac{cạnh \, \, đối}{cạnh \, \, kề}\) và \(\cot \alpha = \dfrac{cạnh \, \, kề}{cạnh \, \, đối}.\)
Lời giải chi tiết
a. Áp dụng công thức lượng giác ta có:
\(\sin \alpha = \dfrac{a}{b};\;\;\cos\alpha = \dfrac{c}{b};\;\tan\alpha = \dfrac{a}{c};\;\;\cot\alpha = \dfrac{c}{a}.\)
Vậy C đúng.
Chọn C.
b. Chọn C sai vì: \(\cosβ = \sin(90°-β)\) nên \(cos β = sin(90°- α)\) là sai, điều này chỉ đúng khi \( β = α=45^o.\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Câu hỏi 4 trang 91 SGK Toán 9 Tập 1
Bài tập 33 trang 93 SGK Toán 9 Tập 1
Bài tập 35 trang 94 SGK Toán 9 Tập 1
Bài tập 36 trang 94 SGK Toán 9 Tập 1
Bài tập 37 trang 94 SGK Toán 9 Tập 1
Bài tập 38 trang 95 SGK Toán 9 Tập 1
Bài tập 39 trang 95 SGK Toán 9 Tập 1
Bài tập 40 trang 95 SGK Toán 9 Tập 1
Bài tập 41 trang 96 SGK Toán 9 Tập 1
-


Chứng minh rằng NE vuông góc AB
bởi Long lanh
 31/01/2019
31/01/2019
Cho đường tròn (O),đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M, BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM.
a. Chứng minh rằng: NE vuông góc AB
b. Gọi F là điểm đối xứng với E qua M. chứng minh rằng FA là tiếp tuyến của (O)
c. chứng minh: FN là tiếp tuyến của đường tròn (B;BA)
d. chứng minh: BM.BF= BF2 -FN2
(Mọi người ai bik câu nào thì giải hộ mk với)
Theo dõi (0) 1 Trả lời -


Chứng minh 20^x - 1 là hợp số với x nguyên, x>1
bởi Ngoc Nga
 31/01/2019
31/01/2019
Chứng minh 20x - 1 là hợp số với x nguên, x>1.
Theo dõi (0) 1 Trả lời -


Chứng minh b+c≥16abc
bởi An Nhiên
 31/01/2019
31/01/2019
cho a,b,c>0 và a+b+c=1. CM: \(b+c\ge16abc\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng 1/a+b+1/b+c+1/a+c≤1/2(1/a+1/b+1/c)
bởi hi hi
 31/01/2019
31/01/2019
Cho a , b , c > 0 Chứng minh rằng: \(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}\le\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh tứ giác ADHE nội tiếp
bởi nguyen bao anh
 31/01/2019
cho tam giác ABC có 3 góc nhọn, góc C= 50 độ nội tiếp đường tròn (0; 2cm). hai đường cao BD và CE cắt nhau tại Ha, chứng minh tứ giác ADHE nội tiếpb, chứng minh tứ giác BEDC nội tiếpc, tính độ dài cung nhỏ ABd, chứng minh đường thưởng OA vuông góc với DEgiải hộ mình với :*Theo dõi (0) 1 Trả lời
31/01/2019
cho tam giác ABC có 3 góc nhọn, góc C= 50 độ nội tiếp đường tròn (0; 2cm). hai đường cao BD và CE cắt nhau tại Ha, chứng minh tứ giác ADHE nội tiếpb, chứng minh tứ giác BEDC nội tiếpc, tính độ dài cung nhỏ ABd, chứng minh đường thưởng OA vuông góc với DEgiải hộ mình với :*Theo dõi (0) 1 Trả lời -


Cho đường tròn (O;R) đường kính AB. Từ A kẻ tiếp tuyến xy với đường tròn, trên xy lấy điểm M, MB cắt đường tròn (O) tại N, gọi H là trung điểm của BN (Toán học - Lớp 9)
a/ chứng minh 4 điểm A, M, H, O cùng nằm trên 1 đường tròn. Xác đinh tâm I
b/ chứng minh BH * BM = 2R^2
Theo dõi (0) 1 Trả lời -


Chứng minh A = n^4 + 4^n là hợp số
bởi Nguyễn Thị Thu Huệ
 31/01/2019
31/01/2019
Cho \(n\in N\) và n>1
Chứng minh: \(A=n^4+4^n\) là hợp số
Theo dõi (0) 1 Trả lời -


Chứng minh AIMK là tứ giác nội tiếp đường tròn
bởi My Le
 31/01/2019
31/01/2019
từ 1 điểm A nằm ngoài (O;R) ta vẽ hai tiếp tuyến AB,AC với đường tròn (B,C là tiếp điểm ).trên cung nhỏ BC lấy một điểm M,vẽ MI vuông góc với AB,MK vuông góc với AC(I thuộc AB,K thuộc AC)
a,chúng minh AIMK là tứ giác nội tiếp đường tròn
b,vẽ MP vuông góc với BC(P thuộc BC).chứng minh góc MPK=góc MBC
c,xác định vị trí điểm M trên cung nhỏ BC để tích MI.MK.MP đạt GTLNTheo dõi (0) 1 Trả lời -


Chứng minh căn(1 + ab) là số hữu tỉ
bởi het roi
 31/01/2019
31/01/2019
cho a, b là số hữu tỉ thỏa mãn (a2+b2-2)(a+b)2+(1-ab)2 =-4ab
chứng minh: \(\sqrt{1+ab}\) là số hữu tỉ
Theo dõi (0) 2 Trả lời -


Chứng minh rằng trong một tam giác nhọn bình phương 1 cạnh bằng tổng bình phương 2 cạnh còn lại trừ 2 lần tích 2 cạnh ấy với cô sin góc xen giữa 2 cạnh
bởi Trần Hoàng Mai
 31/01/2019
31/01/2019
chứng minh rằng trong một tam giác nhọn bình phương 1 cạnh bằng tổng bình phương 2 cạnh còn lại trừ 2 lần tích 2 cạnh ấy với cô sin góc xen giữa 2 cạnh
các bạn giúp mình vs mình cảm ơn
Theo dõi (0) 1 Trả lời -


Chứng minh có ít nhất 1 trong 3 số bằng 1 thỏa mãn abc=1; a + b + c = 1/a + 1/b + 1/c
bởi thanh hằng
 31/01/2019
31/01/2019
cho a,b,c là các số thực thỏa mãn abc=1;\(a+b+c=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\).CMR có ít nhất 1 trong 3 số bằng 1
Theo dõi (0) 1 Trả lời





