OPTADS360
ATNETWORK
ATNETWORK
YOMEDIA

Ôn tập Toán 9 Chương 4 Phương trình bậc hai một ẩn

Để giúp các em học sinh lớp 9 thuận tiện trông quá trinh ôn tập, HỌC247 xin giới thiệu đến các em tài liệu Ôn tập Toán 9 Chương 4 Phương trình bậc hai một ẩn được biên soạn và tổng hợp đầy đủ, bám sát chương trình SGK. Tại đây, hoc247 tóm tắt lại những kiến thức quan trọng và bài tập trọng tâm ở Chương 4. Ngoài ra bộ tài liệu cung cấp nội dung các bài học, hướng dẫn giải bài tập trong SGK, phần trắc nghiệm online có đáp án và hướng dẫn giải cụ thể, chi tiết nhằm giúp các em có thể tham khảo và so sánh với đáp án trả lời của mình. Bên cạnh đó các đề kiểm tra Chương 4 được tổng hợp và sưu tầm từ nhiều trường THCS khác nhau, các em có thể tải file về tham khảo cũng như làm bài thi trực tuyến trên hệ thống để được chấm điểm trực tiếp, từ đó đánh giá được năng lực của bản thân để có kế hoạch ôn tập hiệu quả. Hoc247 hi vọng đây là tài liệu hữu ích giúp các em ôn tập hiệu quả. Chúc các em học tốt. 

ADMICRO/

Đề cương Ôn tập Toán 9 Chương 4

A. Kiến thức cần nhớ

1. Đồ thị hàm số \(y=ax^2 (a\neq 0)\)

Đồ thị hàm số \(y=ax^2 (a\neq 0)\) là tập hợp gồm tất cả các điểm \(M(x_{M}; ax_{M}^{2})\). Để xác định một điểm thuộc đồ thị, ta lấy một giá trị của x làm hoành độ và thay vào phương trình \(y=ax^2\) để tìm ra giá trị tung độ.

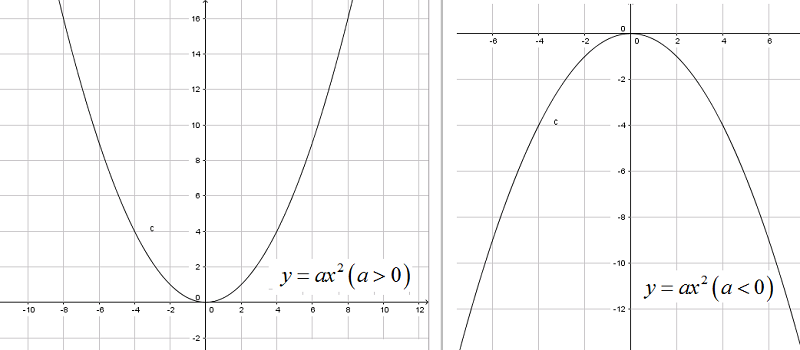
2. Phương trình bậc hai

Phương trình bậc hai một ẩn (gọi tắt là phương trình bậc hai) là phương trình có dạng \(ax^2+bx+c=0\)

 

Trong đó, x là ẩn; các hệ số a, b, c là các số cho trước và  \(a\neq 0\)

3. Công thức nghiệm của phương trình bậc hai

Với phương trình \(ax^2+bx+c=0 (a\neq 0)\) và biệt thức \(\Delta =b^2-4ac\):

\(\Delta>0\) thì phương trình có 2 nghiệm phân biệt:

\(x_{1}=\frac{-b+\sqrt{\Delta }}{2a}\); \(x_{2}=\frac{-b-\sqrt{\Delta }}{2a}\)

\(\Delta=0\) thì phương trình có nghiệm kép \(x=x_{1}=x_{2}=-\frac{b}{2a}\)

\(\Delta<0\) phương trình vô nghiệm.

4. Công thức nghiệm thu gọn

Với các phương trình bậc hai \(ax^2+bx+c=0(a\neq 0)\) và \(b=2b'\), \(\Delta '=b'^2-ac\) thì:

Nếu \(\Delta '>0\) thì phương trình có hai nghiệm phân biệt

\(x_{1}=\frac{-b'+\sqrt{\Delta '}}{a}; x_{2}=\frac{-b'-\sqrt{\Delta '}}{a}\)

Nếu \(\Delta '=0\) thì phương trình có nghiệm kép \(x=\frac{-b'}{a}\)

Nếu \(\Delta '<0\) thì phương trình vô nghiệm.

5. Định lí Vi ét và ứng dụng

Phương trình bậc hai \(ax^2+bx+c=0(a\neq 0)\) có 2 nghiệm phân biệt

\(x_1=\frac{-b+\sqrt{\Delta }}{2a}; x_2=\frac{-b-\sqrt{\Delta }}{2a}\)

Ta có: \(x_1+x_2=\frac{-2b+\sqrt{\Delta }-\sqrt{\Delta }}{2a}=-\frac{b}{a}\)

\(x_1.x_2=\frac{b^2-\Delta }{4a^2}=\frac{4ac}{4a^2}=\frac{c}{a}\)

Định lý Vi-ét

Nếu \(x_1;x_2\) là hai nghiệm của phương trình \(ax^2+bx+c=0 (a\neq 0)\) thì:

\(x_1+x_2=-\frac{b}{a}\)

và \(x_1.x_2=\frac{c}{a}\)

Tổng quát

Nếu phương trình \(ax^2+bx+c=0 (a\neq 0)\) có \(a+b+c=0\) thì phương trình có một nghiệm là \(x_1=1\) và nghiệm kia là \(x_2=\frac{c}{a}\).

Nếu phương trình \(ax^2+bx+c=0 (a\neq 0)\) có \(a-b+c=0\) thì phương trình có một nghiệm là \(x_1=-1\) và nghiệm kia là \(x_2=-\frac{c}{a}\).

6. Các phương trình quy về phương trình bậc hai (phương trình trùng phương, phương trình có ẩn ở mẫu, phương trình tích...)

a. Phương trình trùng phương

Định nghĩa

Phương trình trùng phương là phương trình có dạng: \(ax^4+bx^2+c=0 (a\neq 0)\)

b. Phương trình chứa ẩn ở mẫu

Các bước để giải phương trình chứa ẩn ở mẫu đã học ở lớp 8

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng hai vế rồi khử mẫu

Bước 3: Giải phương trình vừa nhận được 

Bước 4: So sánh điều kiện ban đầu rồi kết luận nghiệm

c. Phương trình tích

Nhắc lại kiến thức đã học ở lớp dưới:

Biến đổi phương trình về dạng \(A.B.C.....=0\) rồi suy ra hoặc \(A=0\) hoặc \(B=0\) hoặc.....

7. Giải toán bằng phương pháp lập phương trình

Phương pháp giải

Để giải bài toán bằng cách lập phương trình, chúng ta làm theo các bước sau:

Bước 1: Lập phương trình

Chọn ẩn và đặt điều kiện cho ẩn

Biểu đạt các đại lượng khác nhau theo ẩn

Dựa vào đề bài toán, lập phương trình theo dạng đã học

Bước 2: Giải phương trình

Bước 3: So sánh kết quả tìm được và chọn nghiệm thích hợp

B. Bài tập minh họa

Bài 1: Cho hàm số \(y=-x^2\) và đường thẳng \(y=-4x+4\). Tìm giao điểm của hai đồ thị đó bằng hình vẽ và đồ thị

Hướng dẫn:Vẽ hình HS tự vẽ.
Tìm giao điểm: Phương trình hoành độ giao điểm: \(-x^2=-4x+4\Leftrightarrow x^2-4x+4=0\)

Tính biệt thức \(\Delta=0\) suy ra phương trình có nghiệm kép x = 2 => y = -4

Vậy khi vẽ hình, ta chỉ nhận được một giao điểm. Sau này lên cấp trên, các em sẽ được biết đường thẳng trên là tiếp tuyến của hàm số.

Bài 2: Giải phương trình bằng cách phân tích đa thức thành nhân tử: \(x^2-11x-12=0\)

Hướng dẫn:\(x^2-11x-12=0\)

\(\Leftrightarrow x^2-12x+x-12=0\)

\(\Leftrightarrow x(x-12)+x-12=0\)

\(\Leftrightarrow (x+1)(x-12)=0\)

Vậy phương trình trên có hai nghiệm phân biệt là \(x=-1;x=12\)

Bài 3: 

Giải phương trình: \(x^2+10x+25=0\); \(x^2-4x-9=0\)

Hướng dẫn: \(x^2+10x+25=0\)

Giải: \(\Delta =10^2-4.1.25=0\) \(\Rightarrow x=\frac{-0}{2}=-5\)

\(x^2-4x-9=0\)

Giải: \(\Delta =(-4)^2-4.1.(-9)=52\Rightarrow \sqrt{\Delta }=2\sqrt{13}>0\)

\(\Rightarrow x_{1}=\frac{-(-4)+2\sqrt{13}}{2}=2+\sqrt{13};x_{2}=\frac{-(-4)-2\sqrt{13}}{2}=2-\sqrt{13}\)

Bài 4: 

Tìm hai số biết hiệu của chúng là 5 và tích của chúng là 150

Hướng dẫn: Gọi hai số cần tim là a, b

Ta có \(\left\{\begin{matrix} a-b=5\\ ab=150 \end{matrix}\right.\)

Thế \(a=5+b\) vào phương trình tích, ta được \(b(b+5)=150\Leftrightarrow b^2+5b-150=0\)

\(\Rightarrow b=-15\) hoặc \(b=10\)

\(b=-15\Rightarrow a=-10\)

\(b=10\Rightarrow a=15\)

Bài 5:

Giải phương trình trùng phương sau: \(x^4-4x^2-5=0\)

Hướng dẫn: Đặt \(t=x^2 (t\geq 0)\)

Khi đó, phương trình trở thành: \(t^2-4t-5=0\)

Giải phương trình bậc hai cơ bản trên, ta được: 

\(t=-1\) (loại)

\(t=5\) (nhận)\(\Rightarrow x=\pm \sqrt{5}\)

Trắc nghiệm Toán 9 Chương 4

Đây là phần trắc nghiệm online theo từng bài học có đáp án và hướng dẫn giải chi tiết.

Đề kiểm tra Toán 9 Chương 4

Đề kiểm tra trắc nghiệm online Chương 4 Toán 9 (Thi Online)

Phần này các em được làm trắc nghiệm online trong thời gian quy định để kiểm tra năng lực và sau đó đối chiếu kết quả và xem đáp án chi tiết từng câu hỏi.

Đề kiểm tra Chương 4 Toán 9 (Tải File)

Phần này các em có thể xem online hoặc tải file đề thi về tham khảo gồm đầy đủ câu hỏi và đáp án làm bài.  

(đang cập nhật)

Lý thuyết từng bài chương 4 và hướng dẫn giải bài tập SGK

Lý thuyết các bài học Toán 9 Chương 4

Hướng dẫn giải bài tập SGK Toán 9 Chương 4

Trên đây là phần nội dung Ôn tập Toán 9 Chương 4 Phương trình bậc hai một ẩn. Hy vọng với tài liệu này, các em sẽ ôn tập tốt và củng cố kiến thức một cách logic. Để thi online và tải file về máy các em vui lòng đăng nhập vào trang hoc247.net và ấn chọn chức năng "Thi Online" hoặc "Tải về". Ngoài ra, các em còn có thể chia sẻ lên Facebook để giới thiệu bạn bè cùng vào học, tích lũy thêm điểm HP và có cơ hội nhận thêm nhiều phần quà có giá trị từ HỌC247 ! 

OFF

XEM NHANH CHƯƠNG TRÌNH LỚP 9