Giải bài 36 tr 94 sách SGK Toán lớp 9 Tập 1
Cho tam giác có một góc bằng 45°. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tính cạnh lớn trong hai cạnh còn lại (lưu ý có hai trường hợp hình 46 và hình 47)
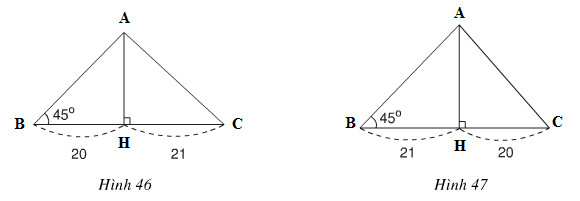
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Trong tam giác vuông, cạnh góc vuông nào có hình chiếu lớn hơn thì cạnh đó lớn hơn.
+) Áp dụng định lý Pi-ta-go.
Lời giải chi tiết
+) Xét hình 46, ta có:
\( BH < HC\,(20cm<21cm) ⇒ AB < AC\) (đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn)
\(∆HAB\) vuông tại \(H\) có \(\widehat{ABH} = 45°\) nên là tam giác vuông cân \(⇒ AH = BH = 20 \, (cm).\)
\(∆HAC\) vuông tại \(H,\) theo định lí Py-ta-go có:
\(AC^2=AH^2+HC^2=21^2+20^2=841=29^2.\)
\( \Rightarrow AC = \sqrt {{29^2}} = 29(cm)\)
Vậy cạnh lớn hơn là \(AC=29cm\)
+) Xét hình 47, ta có:
\( BH > HC\,(21cm>20cm) ⇒ AB > AC\) (đường xiên nào có hình chiếu lớn hơn thì lớn hơn)
\(∆ABH\) vuông tại \(H\) có \(\widehat{B} = 45°\) nên là tam giác vuông cân \(⇒ AH = BH = 21 \, (cm)\)
Theo định lý Py-ta-go trong tam giác vuông \(ABH\) ta có:
\( AB = \sqrt {{{AH}^2} + {{BH}^2}}\)\(= \sqrt {{{21}^2} + {{21}^2}} = 21\sqrt 2 \approx 29,7(cm).\)
Vậy cạnh lớn hơn là \(AB=29,7cm\).
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-
Bài I.5 trang 123 sách bài tập toán 9 tập 1
bởi Lê Bảo An
08/10/2018
Bài I.5 - Bài tập bổ sung (Sách bài tập trang 123)
Cho tam giác ABC vuông tại C có \(\widehat{B}=37^0\). Gọi I là giao điểm của cạnh BC với đường trung trực của AB. Hãy tính AB, AC nếu biết BI = 20
Theo dõi (0) 1 Trả lời -
Bài I.4 trang 123 sách bài tập toán 9 tập 1
bởi Van Tho
08/10/2018
Bài I.4 - Bài tập bổ sung (Sách bài tập trang 123)Hình bình hành ABCD có \(\widehat{A}=120^0,AB=a,BC=b\). Các đường phân giác của bốn góc A, B, C, D cắt nhau tạo thành tứ giác MNPQ. Tính diện tích tứ giác MNPQ ?
Theo dõi (0) 1 Trả lời -
Bài I.3 trang 123 sách bài tập toán 9 tập 1
bởi Nguyễn Phương Khanh
08/10/2018
Bài I.3 - Bài tập bổ sung (Sách bài tập trang 123)
Cho tam giác ABC cân tại A, đường cao BH. Hãy tính góc A và các cạnh AB, BC, nếu biết BH = h, \(\widehat{C}=\alpha\) ?
Theo dõi (0) 1 Trả lời -
Bài I.2 trang 123 sách bài tập toán 9 tập 1
bởi Xuan Xuan
08/10/2018
Bài I.2 - Bài tập bổ sung (Sách bài tập trang 123)
Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính \(\cos\widehat{MAN}\) ?
Theo dõi (0) 1 Trả lời -
ADMICRO
Bài I.1 trang 123 sách bài tập toán 9 tập 1
bởi Anh Trần
08/10/2018
Bài I.1 - Bài tập bổ sung (Sách bài tập trang 123)
Tam giác ABC có \(\widehat{A}=105^0;\widehat{B}=45^0;CB=4cm\). Tính độ dài các cạnh AB, AC ?
Theo dõi (0) 1 Trả lời -
Chứng minh rằng khi a thay đổi (d) luôn cắt (P) tại 2 điểm phân biệt có hoành độ x_1, x_2
bởi truc lam
31/01/2019
Cho hàm số \(y=x^2\)(P) và \(y=-ax+a+2\)(d) (a là tham số)
a) Chứng minh rằng khi a thay đổi (d) luôn cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2.
b) Tìm a để \(\left|x_1-x_2\right|=\sqrt{29}\)
Theo dõi (0) 1 Trả lời -
Chứng minh rằng a+b+c≥α+β+γ
bởi Xuan Xuan
31/01/2019
Với \(\alpha\ge\beta\ge\gamma>0\) , \(a\ge\alpha\) , \(ab\ge\alpha\beta\) , \(abc\ge\alpha\beta\gamma\)
Chứng minh rằng \(a+b+c\ge\alpha+\beta+\gamma\)
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác AMOI nội tiếp và xác định tâm K
bởi thanh duy
31/01/2019
Cho (O) và A nằm ngoài đường tròn. Vẽ tiếp tuyến AM,AN và cát tuyến ACD (tia AO nằm giữa AM và AD). Gọi I là trung điểm của CD.
a/ Chứng minh tứ giác AMOI nội tiếp và xác định tâm K.
b/ Gọi H là giao của MN và AO. Chứng minh tứ giác CHOD nội tiếp.
c/ (K) cvaf (O) cắt nhau tại N. Dây BC vuông góc với MO cắt MN tại F. Chứng minh tứ giác CFIN nội tiếp.
d/Tia DF cắt AM tại E. Chứng minh KE vuông góc với AM.
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác BEHF nội tiếp
bởi Bi do
31/01/2019
Cho tam giác ABC nhọn, nội tiếp đường tròn (O). Vẽ 2 đường cao AE và CF cắt nhau tại H.?
a. Chứng minh tứ giác BEHF nội tiếp
b. Chứng minh tứ giác AFEC nội tiếp
c. Chứng minh đường thẳng OB vuông góc với EF.Theo dõi (0) 1 Trả lời -
Chứng minh độ dài NE không phụ thuộc vào vị trí M
bởi minh vương
31/01/2019
Cho đường tròn (O;R)và (O';r) tiếp xúc ngoài tại A. Trên đường tròn (O) ,vẽ dây cung AB=R, trên cung lớn AB lấy điểm M(M khác A,B),đường thẳng MA cắt đường tròn (O') tại N, qua N kẻ đường thẳng song song với AB, cắt MB tại E
a)CM độ dài NE ko phụ thuộc vào vị trí M
b)tìm vị trí M trên cung AB để diện tích tam giác MNE đạt GTLN/Theo dõi (0) 1 Trả lời -
Bài 99 trang 122 sách bài tập toán 9 tập 1
bởi bala bala
08/10/2018
Bài 99 (Sách bài tập trang 122)Gọi AM , BN, CL là ba đường cao của tam giác ABC. Chứng minh :
a) \(\Delta ANL\) \(\Delta ABC\)
b) AN.BL.CM = AB.BC.CA.cos AcosBcosC
Theo dõi (0) 1 Trả lời
