Giải bài 33 tr 93 sách SGK Toán lớp 9 Tập 1
a) Trong hình 41, sinα bằng
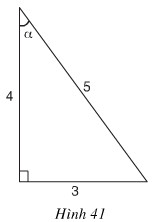
(A) \({5 \over 3}\)
(B) \({5 \over 4}\)
(C) \({3 \over 5}\)
(D) \({3 \over 5}\)
b) Trong hình 42, sin Q bằng
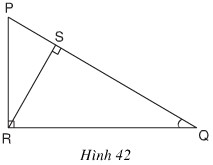
(A) \({{P{\rm{R}}} \over {R{\rm{S}}}}\)
(B) \({{P{\rm{R}}} \over {QR}}\)
(C) \({{P{\rm{S}}} \over {S{\rm{R}}}}\)
(D) \({{S{\rm{R}}} \over {Q{\rm{R}}}}\)
c) Trong hình 43, cos 30° bằng
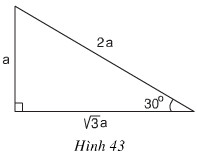
(A) \({{2{\rm{a}}} \over {\sqrt 3 }}\)
(B) \({a \over {\sqrt 3 }}\)
(C) \({{\sqrt 3 } \over 2}\)
(D) \(2\sqrt 3 {a^2}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Dựa vào các tỉ số lượng giác của góc nhọn để làm bài.
\(\sin \alpha = \dfrac{cạnh \, \, đối}{cạnh \, \, huyền}\) và \(\cos \alpha = \dfrac{cạnh \, \, kề}{cạnh \, \, huyền}.\)
Lời giải chi tiết
a. Ta có: \( \displaystyle\sin \alpha = \dfrac{3}{5}.\)
Chọn (C)
b. Xét \( \displaystyle\Delta QPR\) vuông tại R ta có: \( \displaystyle\sin Q = \dfrac{PR}{PQ}.\)
Xét \( \displaystyle\Delta RQS\) vuông tại S ta có: \( \displaystyle\sin Q = \dfrac{RS}{RQ}.\)
Chọn (D)
c. Chọn (C) vì: \( \displaystyle\cos {30^0} = {{\sqrt 3 a} \over {2a}} = {{\sqrt 3 } \over {2}}.\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Câu hỏi 3 trang 91 SGK Toán 9 Tập 1
Câu hỏi 4 trang 91 SGK Toán 9 Tập 1
Bài tập 34 trang 93 SGK Toán 9 Tập 1
Bài tập 35 trang 94 SGK Toán 9 Tập 1
Bài tập 36 trang 94 SGK Toán 9 Tập 1
Bài tập 37 trang 94 SGK Toán 9 Tập 1
Bài tập 38 trang 95 SGK Toán 9 Tập 1
Bài tập 39 trang 95 SGK Toán 9 Tập 1
Bài tập 40 trang 95 SGK Toán 9 Tập 1
Bài tập 41 trang 96 SGK Toán 9 Tập 1
-


Chứng minh rằng với ba số tự nhiên a,b,c trong đó có đúng một số lẻ và hai số chẵn ta luôn có (a+b+c)^3−(a+b−c)^3−(b+c−a)^3−(a+c−b)3⋮96
bởi Nguyễn Minh Hải
 31/01/2019
31/01/2019
Chứng minh rằng với ba số tự nhiên a,b,c trong đó có đúng một số lẻ và hai số chẵn ta luôn có:
\(\left(a+b+c\right)^3-\left(a+b-c\right)^3-\left(b+c-a\right)^3-\left(a+c-b\right)^3⋮96\)
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác ABOC nội tiếp
bởi trang lan
 31/01/2019
31/01/2019
cho(o) từ 1 điểm A nằm ngoài đg tròn vẽ 2 tiếp tuyến AB và AC với đg tròn .kẻ dây AD cắt đg tròn tại E a,cm tứ giác ABOC nội tiếp
b.cm AB bình =AE nhanAD
Theo dõi (0) 1 Trả lời -


Chứng minh tồn tại một số chia hết cho 2009 và tổng các chữ số của nó nằng 2010
bởi Tieu Dong
 31/01/2019
31/01/2019
CMR tồn tại một số chia hết cho 2009 và tổng các chữ số của nó nằng 2010
Theo dõi (0) 1 Trả lời -


Tính các canh của tam giac ABC và đường cao AH theo R
bởi Trieu Tien
 31/01/2019
31/01/2019
Cho tam giác ABC đêu nội tiếp đường tròn tâm O bán kính R
A, Tính các canh của tam giac ABCva đường cao AH theo R
B, Gọi M là điểm di động trên cung nhỏ BC ( M không trùng với B và C )
Trên tia đối của tia MB lấy điểm D sao cho MD=MC . Chứng minh tam giác CDM đều
C, Tìm vị trí của điểm M sao cho MA+MB+MC lớn nhất và chứng minh điều đó
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh rằng căn(2012a+(b−c)^2/2)+căn(2012b+(c−a)^2/2)+căn(2012c+(a−b)^2/2/)≤2012căn2
bởi hồng trang
 31/01/2019
31/01/2019
Cho a,b,c không âm thỏa mãn: a + b + c = 1006
Chứng minh rằng : \(\sqrt{2012a+\dfrac{\left(b-c\right)^2}{2}}+\sqrt{2012b+\dfrac{\left(c-a\right)^2}{2}}+\sqrt{2012c+\dfrac{\left(a-b\right)^2}{2}}\le2012\sqrt{2}\)
Theo dõi (0) 1 Trả lời -


cho các số thực dương x,y,z thỏa x+2y+3z=18 CMR
\(\dfrac{2y+3z+5}{1+x}+\dfrac{3z+x+5}{1+2y}+\dfrac{x+2y+5}{1+3z}\ge\dfrac{51}{7}\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng tam giác ABC vuông tại A
bởi Nguyen Ngoc
 13/02/2019
13/02/2019
Cho \(\Delta ABC\) và đường cao AH. \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\). CM : \(\Delta ABC\) vuông tại A.
Hung nguyen,Xuân Tuấn Trịnh,Ace Legona,Nguyễn Trần Thành Đạt.......
Theo dõi (0) 1 Trả lời -


Chứng minh rằng a^2 + b^2 + c^2 < 2(1 - abc)
bởi Van Tho
 31/01/2019
31/01/2019
Cho a, b, c là 3 cạnh của 1 tam giác có chu vi bằng 2. Chứng minh rằng
a2 + b2 + c2 < 2(1 - abc)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng AB^2 +AC^2=2AM2+ BC^2/2
bởi My Hien
 31/01/2019
31/01/2019
cho tam giác ABC trung tuyến AM . chứng minh rằng AB2 +AC2=2AM2+\(\frac{BC^2}{2}\)
Theo dõi (0) 1 Trả lời -


cho x,y,z >0 thỏa \(x^2+y^2+z^2=3\) CMR
\(\dfrac{x}{\sqrt[3]{yz}}+\dfrac{y}{\sqrt[3]{xz}}+\dfrac{z}{\sqrt[3]{xy}}\ge xy+yz+xz\)
Theo dõi (0) 1 Trả lời -


CMR
\(\dfrac{1}{1^2+2^2}+\dfrac{1}{2^2+3^2}+\dfrac{1}{3^2+4^2}+...+\dfrac{1}{2016^2+2017^2}< \dfrac{1}{2}\)
Theo dõi (0) 1 Trả lời






