Giải bài 1 tr 91 sách SGK Toán lớp 9 Tập 1
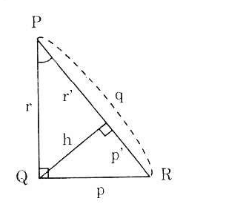
Cho hình 36. Hãy viết hệ thức giữa:
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
b) Các cạnh góc vuông p, r và đường cao h.
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
Hướng dẫn giải chi tiết
Phương pháp giải
Áp dụng hệ thức lượng trong tam giác vuông
Lời giải chi tiết
\(\begin{array}{l}
a)\,{p^2} = p'.q;\,{r^2} = r'.q\\
b)\,\dfrac{1}{{{h^2}}} = \dfrac{1}{{{p^2}}} + \dfrac{1}{{{r^2}}}\\
c)\,{h^2} = p'.r'
\end{array}\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 97 trang 122 SBT Toán 9 Tập 1
Bài tập 98 trang 122 SBT Toán 9 Tập 1
Câu hỏi 2 trang 91 SGK Toán 9 Tập 1
Câu hỏi 3 trang 91 SGK Toán 9 Tập 1
Câu hỏi 4 trang 91 SGK Toán 9 Tập 1
Bài tập 33 trang 93 SGK Toán 9 Tập 1
Bài tập 34 trang 93 SGK Toán 9 Tập 1
Bài tập 35 trang 94 SGK Toán 9 Tập 1
Bài tập 36 trang 94 SGK Toán 9 Tập 1
Bài tập 37 trang 94 SGK Toán 9 Tập 1
Bài tập 38 trang 95 SGK Toán 9 Tập 1
Bài tập 39 trang 95 SGK Toán 9 Tập 1
Bài tập 40 trang 95 SGK Toán 9 Tập 1
Bài tập 41 trang 96 SGK Toán 9 Tập 1
-


Cho a,b, c là các số thực dương thỏa mãn a+b+c=3. CMR:
\(\dfrac{1}{a^2+b^2+2}+\dfrac{1}{b^2+c^2+2}+\dfrac{1}{c^2+a^2+2}\le\dfrac{3}{4}\)
Theo dõi (0) 1 Trả lời -


Cho x,y,z là các số thực dương. Chứng minh rằng:
\(\dfrac{1}{x^3+y^3+xyz}+\dfrac{1}{y^3+z^3+xyz}+\dfrac{1}{z^3+x^3+xyz}\le\dfrac{1}{xyz}\)
Theo dõi (0) 1 Trả lời -


Cho hình chữ nhật ABCD có chiều dài AB =2a chiều rộng BC=a.kẻ tia phân giác của góc ACD tu A hạ AH vuông góc với đường phân giác nói trên
1, C/M; BDCE nội tiếp xác định tâm của đường tròn này.
2C/M ;AMvuông góc DE
Theo dõi (0) 1 Trả lời -


Tính diện tích hình thang, biết AB=26cm; CD=10cm
bởi Nguyễn Bảo Trâm
 12/02/2019
12/02/2019
cho hình thang cân ABCD biết AB=26cm; CD=10cm, đường chéo AC vuông góc với AD. tính điện tích hình thang
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh trong a,b,c tồn tại một số bằng 3
bởi Tra xanh
 30/01/2019
30/01/2019
a+b+c=3 và \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{3}\) Chứng minh trong a,b,c tồn tại một số bằng 3
Theo dõi (0) 1 Trả lời -


Chứng minh các công thức sin2α = 2 sin α . cos α
bởi Nguyễn Minh Minh
 12/02/2019
12/02/2019
Cho tam giác ABC vuông tại A, AB < AC, góc \(C=\alpha< 45^o\) , đường trung tuyến AM, đường cao AH, MA = MB = MC = \(\alpha\). Chứng minh các công thức :
a) \(\sin2\alpha=2\sin\alpha.\cos\alpha\)
b) \(1+\cos2\alpha+2\cos^2\alpha\)
c) \(1-\cos2\alpha=2\sin^2\alpha\)
d) \(\sin^2\alpha+\cos^2\alpha=1\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng m^2 + n^2 + 2 ⋮ 4 mn
bởi thu trang
 30/01/2019
30/01/2019
cho 2 số nguyên dương lẻ m,n nguyên tố cùng nhau và
\(\left\{{}\begin{matrix}m^2+2⋮n\\n^2+2⋮m\end{matrix}\right.\)
chứng minh rằng \(m^2+n^2+2⋮4mn\)
Theo dõi (0) 1 Trả lời -


Tính độ dài cạnh BC, có AB = 6cm, đường cao AH = 3cm
bởi A La
 13/02/2019
13/02/2019
Cho tam giác ABC vuông tại A, có AB = 6cm, đường cao AH = 3cm. Tính độ dài cạnh BC.
Theo dõi (0) 1 Trả lời -


Chứng minh NE vuông góc với AB
bởi Duy Quang
 30/01/2019
30/01/2019
Cho đường tròn (O), đường kính AB,điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM
a) chứng minh NE vuông góc với AB
b) gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O)
Theo dõi (0) 1 Trả lời -


Chứng minh BI^2/CI2 = BM/CN
bởi thi trang
 13/02/2019
13/02/2019
Tam giác ABC có I là giao điểm của ba đường phân giác. Qua I kẻ đường thẳng vuông góc với IA cẳ AB tại M, AC tại N.
a) Chứng minh \(\dfrac{BI^2}{CI^2}=\dfrac{BM}{CN}\)
b)chứng minh BM.AC - NC.AB + A\(I^2\) = AB.AC
Theo dõi (0) 1 Trả lời -


So sánh cotg N và cotg P
bởi bich thu
 13/02/2019
13/02/2019
Đường cao MQ của tam giác vuông MNP chia cạnh huyền NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotg N và cotg P. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần ?
Theo dõi (0) 1 Trả lời





