Bài tập 41 tr 129 sách GK Toán lớp 9 Tập 2
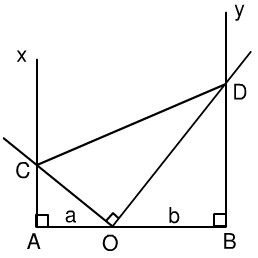
Cho ba điểm \(A, O, B\) thẳng hàng theo thứ tự đó, \(OA = a, OB = b\) (\(a,b\) cùng đơn vị: cm).
Qua \(A\) và \(B\) vẽ theo thứ tự các tia \(Ax\) và \(By\) cùng vuông góc với \(AB\) và cùng phía với \(AB\). Qua \(O\) vẽ hai tia vuông góc với nhau và cắt \(Ax\) ở \(C\), \(By\) ở \(D\) (xem hình 116).
a) Chứng minh \(AOC\) và \(BDO\) là hai tam giác đồng dạng; từ đó suy ra tích \(AC.BD\) không đổi.
b) Tính diện tích hình thang \(ABDC\) khi \(\widehat {COA} = {60^0}\)
c) Với \(\widehat {COA} = {60^0}\) cho hình vẽ quay xung quanh \(AB\). Hãy tính tỉ số tích các hình do các tam giác \(AOC\) và \(BOD\) tạo thành
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) Hai tam giác có hai cặp góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.
b) Công thức tính diện tích hình thang có đáy lớn là \(a,\) đáy nhỏ là \(b\) và chiều cao \(h\) là: \(S = \dfrac{{\left( {a + b} \right)h}}{2}.\)
c) Thể tích hình nón: \( V = \dfrac{1}{3}\pi {r^2}h.\)
Lời giải chi tiết
a) Xét hai tam giác vuông \(AOC\) và \(BDO\) ta có: \(\widehat A = \widehat B = {90^0}\)
\(\widehat {AOC} = \widehat {B{\rm{D}}O}\) (cùng phụ với \(\widehat{BOD}\)).
Vậy \(∆AOC\) đồng dạng \(∆BDO \, \, (g-g).\)
\( \displaystyle \Rightarrow {{AC} \over {AO}} = {{BO} \over {B{\rm{D}}}} \, \, hay \, \, {{AC} \over a} = {b \over {B{\rm{D}}}}.\) (1)
Vậy \(AC . BD = a . b \) không đổi.
b) Khi \(\widehat {COA} = 60^\circ \) , xét tam giác vuông \(ACO\) ta có \(\tan \widehat {AOC} = \dfrac{{AC}}{{OA}} \Rightarrow \tan 60^\circ = \dfrac{{AC}}{a} \Rightarrow AC = a\sqrt 3 \)
mà \(AC.BD = ab\) (câu a) nên \(a\sqrt 3 .BD = ab \Rightarrow BD = \dfrac{{b\sqrt 3 }}{3}\)
Ta có công thức tính diện tích hình thang \(ABCD\) là:
\(\eqalign{
& S = {{AC + B{\rm{D}}} \over 2}.AB = \displaystyle {{a\sqrt 3 + {{b\sqrt 3 } \over 3}} \over 2}.\left( {a + b} \right) \cr
& = {{\sqrt 3 } \over 6}\left( {3{{\rm{a}}^2} + 4{\rm{a}}b + {b^2}} \right)\left( {c{m^2}} \right) \cr} \)
c) Theo đề bài ta có:
Tam giác \(AOC\) khi quay quanh cạnh \(AB\) tạo thành hình nón có chiều cao \(OA = a\) và bán kính đáy \(AC = a\sqrt 3 \) nên thể tích hình nón là \({V_1} = \dfrac{1}{3}\pi .OA.A{C^2} = \dfrac{1}{3}\pi .a.{\left( {a\sqrt 3 } \right)^2} = \pi {a^3}\left( {c{m^3}} \right)\)
Tam giác \(BOD\) khi quay quanh cạnh \(AB\) tạo thành hình nón có chiều cao \(OB = b\) và bán kính đáy \(BD = \dfrac{{b\sqrt 3 }}{3}\) nên thể tích hình nón là \({V_2} = \dfrac{1}{3}\pi .OB.B{D^2} = \dfrac{1}{3}\pi .b.{\left( {\dfrac{{b\sqrt 3 }}{3}} \right)^2} = \dfrac{{\pi {b^3}}}{9}\left( {c{m^3}} \right)\)
Do đó \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\pi {a^3}}}{{\dfrac{{\pi {b^3}}}{9}}} = \dfrac{{9{a^3}}}{{{b^3}}}\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 39 trang 129 SGK Toán 9 Tập 2
Bài tập 40 trang 129 SGK Toán 9 Tập 2
Bài tập 42 trang 130 SGK Toán 9 Tập 2
Bài tập 43 trang 130 SGK Toán 9 Tập 2
Bài tập 44 trang 130 SGK Toán 9 Tập 2
Bài tập 42 trang 174 SBT Toán 9 Tập 2
Bài tập 43 trang 174 SBT Toán 9 Tập 2
Bài tập 44 trang 174 SBT Toán 9 Tập 2
Bài tập 45 trang 174 SBT Toán 9 Tập 2
Bài tập 46 trang 175 SBT Toán 9 Tập 2
Bài tập 47 trang 175 SBT Toán 9 Tập 2
Bài tập 48 trang 175 SBT Toán 9 Tập 2
Bài tập 49 trang 175 SBT Toán 9 Tập 2
Bài tập IV.1 trang 176 SBT Toán 9 Tập 2
Bài tập IV.2 trang 176 SBT Toán 9 Tập 2
Bài tập IV.3 trang 176 SBT Toán 9 Tập 2
Bài tập IV.4 trang 177 SBT Toán 9 Tập 2
-


Có hình vuông ABCD cạnh bằng a. Gọi E là trung điểm của CD. Tính độ dài dây cung chung CF của đường tròn đường kính BE và đường tròn đường kính CD.
bởi Vương Anh Tú
 11/07/2021
11/07/2021
A. \(CF = a.\)
B. \(CF = \dfrac{{2a\sqrt 5 }}{5}.\)
C. \(CF = \dfrac{{2a\sqrt 3 }}{3}.\)
D. \(CF = \dfrac{{a\sqrt 5 }}{5}.\)
Theo dõi (0) 1 Trả lời -


Cho biết \(\widehat {xOy} = {45^0}.\) Trên tia Oy lấy hai điểm A, B sao cho \(AB = \sqrt 2 \left( {cm} \right).\) Tính độ dài hình chiếu vuông góc của đoạn thẳng AB trên Ox.
bởi Thùy Nguyễn
 11/07/2021
11/07/2021
A. \(\dfrac{{\sqrt 2 }}{2}\left( {cm} \right).\)
B. \(\dfrac{{\sqrt 2 }}{4}\left( {cm} \right).\)
C. \(1\left( {cm} \right).\)
D. \(\dfrac{1}{2}\left( {cm} \right).\)
Theo dõi (0) 1 Trả lời -


Cho mặt cầu (S) được gọi là ngoại tiếp hình lập phương ABCD.A’B’C’D’ nếu các đỉnh của hình laapoj phương đều thuộc mặt cầu (S). Biết hình lập phương có độ dài cạnh 2a, tính thể tích V của hình cầu ngoại tiếp hình lập phương đó.
bởi Thuy Kim
 11/07/2021
11/07/2021
A. \(V = 3\pi {a^3}.\)
B. \(V = 4\sqrt 3 \pi {a^3}.\)
C. \(V = \dfrac{{\sqrt 3 }}{2}\pi {a^3}.\)
D. \(V = 3\sqrt 2 \pi {a^3}.\)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, biết \(\widehat B = {60^0},AB = 6\left( {cm} \right),BC = 4\left( {cm} \right).\) Cho biết độ dài của cạnh AC.
bởi Nguyễn Tiểu Ly
 12/07/2021
12/07/2021
A. \(AC = 2\sqrt 7 \left( {cm} \right).\)
B. \(AC = \sqrt {52} \left( {cm} \right).\)
C. \(AC = 4\sqrt 5 \left( {cm} \right).\)
D. \(AC = 2\sqrt 3 \left( {cm} \right).\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho biết các cạnh của một tứ giác tỉ lệ với 2; 3; 4; 5 và độ dài cạnh lớn nhất hơn độ dài cạnh nhỏ nhất là 6(cm). Tính chu vi của tứ giác đó.
bởi Hong Van
 11/07/2021
11/07/2021
A. 28 (cm).
B. 42 (cm).
C. 14 (cm)
D. 56 (cm).
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có AB = 20(cm), BC = 12 (cm), CA = 16 (cm). Hãy tính chu vi của đường tròn nội tiếp tam giác đã cho.
bởi Minh Hanh
 12/07/2021
12/07/2021
A. \(16\pi \left( {cm} \right).\)
B. \(20\pi \left( {cm} \right).\)
C. \(13\pi \left( {cm} \right).\)
D. \(8\pi \left( {cm} \right).\)
Theo dõi (0) 1 Trả lời -


Có tam giác ABC vuông tại A, đường cao AH và đường trung tuyến AM \(\left( {H,M \in BC} \right)\) . Biết chu vi của tam giác là 72cm và AM – AH = 7 (cm). Tính diện tích S của tam giác ABC.
bởi Phung Hung
 12/07/2021
12/07/2021
A. \(S = 48\left( {c{m^2}} \right)\)
B. \(S = 108\left( {c{m^2}} \right)\)
C. \(S = 148\left( {c{m^2}} \right)\)
D. \(S = 144\left( {c{m^2}} \right)\)
Theo dõi (0) 1 Trả lời -


A. 25(cm)
B. 24(cm).
C. 30 (cm).
D. 15 (cm).
Theo dõi (0) 1 Trả lời -


Cho một hình cầu có đường kính là bằng 4 (cm). Tính diện tích S của hình cầu đó.
bởi Mai Linh
 12/07/2021
12/07/2021
A. \(S = \dfrac{{16\pi }}{3}\left( {c{m^2}} \right)\) .
B. \(S = 16\pi \,\left( {c{m^2}} \right)\)
C. \(S = 64\pi \,\left( {c{m^2}} \right)\)
D. \(S = 32\pi \,\left( {c{m^2}} \right)\)
Theo dõi (0) 1 Trả lời -


A. \(r = \dfrac{{a\sqrt 3 }}{6}.\)
B. \(r = a\sqrt 3 .\)
C. \(r = \dfrac{{a\sqrt 3 }}{3}.\)
D. \(r = \dfrac{{2a\sqrt 3 }}{3}.\)
Theo dõi (0) 1 Trả lời






