Bài tập 39 tr 129 sách GK Toán lớp 9 Tập 2
Một hình chữ nhật \(ABCD\) có \(AB > AD\), diện tích và chu vi của nó theo thứ tự là \(2a^2\) và \(6a\). Cho hình vẽ quay xung quanh cạnh \(AB\), ta được một hình trụ.
Tính diện tích xung quanh và thể tích của hình trụ này.
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Quay hình chữ nhật quanh một cạnh cố định của nó ta được một hình trụ.
+) Chu vi hình chữ nhật có kích thước \(a, \, b\) là: \(C=2(a+b).\)
+) Diện tích hình chữ nhật có kích thước \(a, \, b\) là: \(S=ab.\)
+) Diện tích xung quanh của hình trụ: \(S_{xq}=2\pi rh.\)
+) Thể tích hình trụ là: \(V=\pi r^2h.\)
Lời giải chi tiết
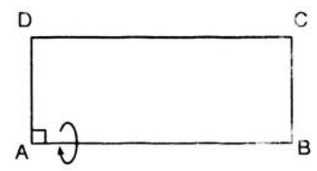
Theo đề bài ta có:
Diện tích hình chữ nhật \(ABCD\) là: \(AB.AD = 2a^2\) (1)
Chu vi hình chữ nhật là: \(2(AB + CD) = 6a ⇒ AB + CD = 3a\) (2)
Từ (1) và (2), ta có \(AB\) và \(CD\) là nghiệm của phương trình:
\({x^2}-{\rm{ }}3ax{\rm{ }}+{\rm{ }}2{a^2} = {\rm{ }}0\)
\(\begin{array}{l}
{x^2} - ax - 2ax + 2{a^2} = 0\\
\Leftrightarrow x\left( {x - a} \right) - 2a\left( {x - a} \right) = 0\\
\Leftrightarrow \left( {x - a} \right)\left( {x - 2a} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = a\\
x = 2a
\end{array} \right.
\end{array}\)
Theo giả thiết \(AB > AD\) nên ta chọn \(AB = 2a; AD = a\)
Khi quay hình chữ nhật quanh \(AB\) ta được hình trụ có \(h=AB=2a\) và \(r=AD=a.\)
Vậy diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi .AD.AB = 2\pi .a.2a = 4{\rm{ }}\pi {a^2}\)
Thể tích hình trụ là:
\(V{\rm{ }} = {\rm{ }}\pi {\rm{ }}.{\rm{ }}A{D^2}.{\rm{ }}AB{\rm{ }} = {\rm{ }}\pi .{\rm{ }}{a^2}.{\rm{ }}2a{\rm{ }} = {\rm{ }}2\pi {a^3}\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 38 trang 129 SGK Toán 9 Tập 2
Bài tập 40 trang 129 SGK Toán 9 Tập 2
Bài tập 41 trang 129 SGK Toán 9 Tập 2
Bài tập 42 trang 130 SGK Toán 9 Tập 2
Bài tập 43 trang 130 SGK Toán 9 Tập 2
Bài tập 44 trang 130 SGK Toán 9 Tập 2
Bài tập 42 trang 174 SBT Toán 9 Tập 2
Bài tập 43 trang 174 SBT Toán 9 Tập 2
Bài tập 44 trang 174 SBT Toán 9 Tập 2
Bài tập 45 trang 174 SBT Toán 9 Tập 2
Bài tập 46 trang 175 SBT Toán 9 Tập 2
Bài tập 47 trang 175 SBT Toán 9 Tập 2
Bài tập 48 trang 175 SBT Toán 9 Tập 2
Bài tập 49 trang 175 SBT Toán 9 Tập 2
Bài tập IV.1 trang 176 SBT Toán 9 Tập 2
Bài tập IV.2 trang 176 SBT Toán 9 Tập 2
Bài tập IV.3 trang 176 SBT Toán 9 Tập 2
Bài tập IV.4 trang 177 SBT Toán 9 Tập 2
-
Cho tam giác ABC có AB = 4cm, AC = 6cm. Trên các cạnh AB và AC lần lượt lấy các điểm D và E sao cho BD = CE. Đường thẳng DE cắt đường thẳng BC tại điểm I. Tính tỷ số IE/ID
bởi Denki Kaminari
28/07/2021
Cho tam giác ABC có AB = 4cm, AC = 6cm. Trên các cạnh AB và AC lần lượt lấy các
điểm D và E sao cho BD = CE. Đường thẳng DE cắt đường thẳng BC tại điểm I. Tính
tỷ số IE/IDTheo dõi (0) 1 Trả lời -
Cho tam giác ABC vuông tại A, có BC=a, AC=b, AB=c. Giải tam giác vuông ABC biết rằng b=28cm, c=21cm
bởi Lê Thảo
28/07/2021
Cho tam giác ABC vuông tại A, có BC=a, AC=b, AB=c. Giải tam giác vuông ABC biết rằng
a) b=28cm, c=21cm
b) a=10cm, b=6cm
Theo dõi (0) 0 Trả lời -
cho tam giác ABC vuông tại A, AH là đường cao. biết AB=12, CH=12,8 . Tính các cạnh còn lại.
bởi Nguyệt Ánh
27/07/2021
cho tam giác ABC vuông tại A, AH là đường cao. biết AB=12, CH=12,8 .tính các cạnh còn lại
Theo dõi (0) 1 Trả lời -
Với hình chữ nhật \(ABCD\) có \(AB = 2\sqrt 3 \;cm,\;\;BC = 2\;cm.\) Độ dài đường kính của đường tròn ngoại tiếp hình chữ nhật \(ABCD\) bằng:
bởi Naru to
11/07/2021
A. \(2\;cm\)
B. \(2\sqrt 3 \;cm\)
C. \(4\;cm\)
D. \(8\;cm\)
Theo dõi (0) 2 Trả lời -
ADMICRO
Có tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của BC. Biết AB = 3 cm, AC = 4cm. Tính độ dài đường cao AH và diện tích tam giác ABM.
bởi Minh Thắng
12/07/2021
Có tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của BC. Biết AB = 3 cm, AC = 4cm. Tính độ dài đường cao AH và diện tích tam giác ABM.
Theo dõi (0) 1 Trả lời -
Ta có hình trụ có diện tích xung quanh bằng \(256\pi c{m^2}\) và bán kính đáy bằng \(\dfrac{1}{2}\) đường cao. Tính bán kính đáy và thể tích hình trụ.
bởi Nguyễn Lê Thảo Trang
12/07/2021
Ta có hình trụ có diện tích xung quanh bằng \(256\pi c{m^2}\) và bán kính đáy bằng \(\dfrac{1}{2}\) đường cao. Tính bán kính đáy và thể tích hình trụ.
Theo dõi (0) 1 Trả lời -
Với đường tròn tâm O, dây cung AB không đi qua tâm O. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây cung MC không đi qua tâm O cắt đoạn thẳng AB tại D (D khác A, D khác B). Đường thẳng vuông góc với AB tại D, cắt OC tại K.Chứng minh rằng tam giác KCD là tam giác đều.
bởi Phạm Phú Lộc Nữ
12/07/2021
Với đường tròn tâm O, dây cung AB không đi qua tâm O. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây cung MC không đi qua tâm O cắt đoạn thẳng AB tại D (D khác A, D khác B). Đường thẳng vuông góc với AB tại D, cắt OC tại K.Chứng minh rằng tam giác KCD là tam giác đều.
Theo dõi (0) 1 Trả lời -
Ta có hai đường tròn \(\left( {O;\;4cm} \right)\) và \(\left( {O';\;11cm} \right).\) Biết khoảng cách \(OO' = 2a + 3\;\left( {cm} \right)\) với \(a\) là số thực dương. Tìm \(a\) để hai đường tròn tiếp xúc nhau.
bởi Hồng Hạnh
12/07/2021
Ta có hai đường tròn \(\left( {O;\;4cm} \right)\) và \(\left( {O';\;11cm} \right).\) Biết khoảng cách \(OO' = 2a + 3\;\left( {cm} \right)\) với \(a\) là số thực dương. Tìm \(a\) để hai đường tròn tiếp xúc nhau.
Theo dõi (0) 1 Trả lời -
Có tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH,\) biết \(AC = 16cm\) và \(\sin \widehat {CAH} = \dfrac{4}{5}.\) Tính độ dài các cạnh \(BC,\;AB.\)
bởi Huong Duong
12/07/2021
Có tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH,\) biết \(AC = 16cm\) và \(\sin \widehat {CAH} = \dfrac{4}{5}.\) Tính độ dài các cạnh \(BC,\;AB.\)
Theo dõi (0) 1 Trả lời -
Ta có 1 mảnh đất hình chữ nhật có diện tích \(360{m^2}.\) Nếu tăng chiều rộng \(2m\) và giảm chiều dài \(6m\) thì diện tích mảnh đất không đổi. Tính chu vi của mảnh đất lúc đầu.
bởi minh thuận
12/07/2021
Ta có 1 mảnh đất hình chữ nhật có diện tích \(360{m^2}.\) Nếu tăng chiều rộng \(2m\) và giảm chiều dài \(6m\) thì diện tích mảnh đất không đổi. Tính chu vi của mảnh đất lúc đầu.
Theo dõi (0) 1 Trả lời
