Bài tập 38 tr 129 sách GK Toán lớp 9 Tập 2
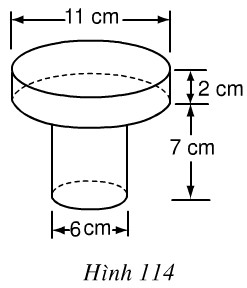
Hãy tính thể tích , diện tích bề mặt một chi tiết máy theo kích thước đã cho trên hình 114.
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Diện tích xung quanh của hình trụ: \(S_{xq}=2\pi rh.\)
+) Diện tích toàn phần của hình trụ: \(S_{tp}=2 \pi rh +2 \pi r^2.\)
+) Thể tích hình trụ là: \(V=\pi r^2h.\)
Lời giải chi tiết
* Ta có: Thể tích phần cần tính là tổng thể tích của hai hình trụ có đường kính là \(11cm\) và chiều cao là \(2cm\).
\(\displaystyle {V_1} = \pi {R^2}{h_1} = \pi {\left( {{{11} \over 2}} \right)^2}.2 = 60,5\pi \left( {c{m^3}} \right)\)
Thể tích hình trụ có đường kính đáy là \(6cm\), chiều cao là \(7cm\)
\(\displaystyle {V_2} = \pi {R^2}{h_2} = \pi {\left( {{6 \over 2}} \right)^2}.7 = 63\pi \left( {c{m^3}} \right)\)
Vậy thể tích của chi tiết máy cần tính là:
\(V = {V_1} + {V_2} = 60,5\pi + 63\pi = 123,5\pi (c{m^3})\)
* Tương tự, theo đề bài diện tích bề mặt của chi tiết máy bằng tổng diện tích xung quanh của hai chi tiết máy với diện tích 2 hình tròn đáy của hình trụ nằm trên.
Diện tích toàn phần của hình trụ có đường kính đáy \(11 cm\), chiều cao là \(2cm\) và là:
\({S_{tp(1)}} = 2\pi R_1{h_1} + 2\pi {R_1}^2 \)
\(\displaystyle = 2\pi {{11} \over 2}.2 + 2\pi .5,5^2 = 82,5 \pi \left( {c{m^2}} \right)\)
Diện tích xung quanh của hình trụ có đường kính đáy là \(6cm\) và chiều cao là \(7cm\) là:
\(\displaystyle {S_{xq(2)}} = 2\pi R_2 {h_2} = 2\pi {6 \over 2}.7 = 42\pi \left( {c{m^2}} \right)\)
Vậy diện tích bề mặt của chi tiết máy là:
\(S = {S_{tp(1)}} + {\rm{ }}{S_{xq(2)}} = 82,5\pi + 42\pi = 124,5\pi (c{m^2}).\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 39 trang 129 SGK Toán 9 Tập 2
Bài tập 40 trang 129 SGK Toán 9 Tập 2
Bài tập 41 trang 129 SGK Toán 9 Tập 2
Bài tập 42 trang 130 SGK Toán 9 Tập 2
Bài tập 43 trang 130 SGK Toán 9 Tập 2
Bài tập 44 trang 130 SGK Toán 9 Tập 2
Bài tập 42 trang 174 SBT Toán 9 Tập 2
Bài tập 43 trang 174 SBT Toán 9 Tập 2
Bài tập 44 trang 174 SBT Toán 9 Tập 2
Bài tập 45 trang 174 SBT Toán 9 Tập 2
Bài tập 46 trang 175 SBT Toán 9 Tập 2
Bài tập 47 trang 175 SBT Toán 9 Tập 2
Bài tập 48 trang 175 SBT Toán 9 Tập 2
Bài tập 49 trang 175 SBT Toán 9 Tập 2
Bài tập IV.1 trang 176 SBT Toán 9 Tập 2
Bài tập IV.2 trang 176 SBT Toán 9 Tập 2
Bài tập IV.3 trang 176 SBT Toán 9 Tập 2
Bài tập IV.4 trang 177 SBT Toán 9 Tập 2
-
Cho ABC nhọn ( AB < AC ) nội tiếp đường tròn (0;R) Hai đường cao BM và CN cắt nhau tai H, AH cắt BC tai D. CMR: tứ giác ANHM nội tiếp và AH vuông góc BC tại D.
bởi Ngọc Nguyễn
28/01/2023
Giải giúp mình bài này nhé! Cho ABC nhon ( AB < AC ) nội tiếp đường tròn (0;R) Hai đường cao BM và CN cắt nhau tai H, AH cắt BC tai D. a) CMR: tứ giác ANHM nội tiếp và AH vuông góc BC tại D. b) CMR AM .AC = AN. AB Nếu BC = 2MN chứng minh góc ACN = 30⁰ c) Kẻ đường kính BK của (O) CMR AH= KC d) CMR H,I,Q thẳng hàng biết AQ là đường kính của (O) I là trung điểm của BCTheo dõi (0) 0 Trả lời -
Cho tam giác ABC có góc A > 90 độ. Đường tròn nội tiếp tam giác lần lượt tiếp xúc với AB, AC tại M,N. Lấy D, E lần lượt trên tia đối AB,AC sao cho BD=CE=BC. Gọi giao điểm của MN với BE, CD lần lượt lag P, Q. Chứng minh P, Q lần lượt là trung điểm BE,CD.
bởi Lê Vy
09/01/2023
Cho tam giác ABC có góc A > 90 độ. Đường tròn nội tiếp tam giác lần lượt tiếp xúc với AB,AC tại M,N. Lấy D,E lần lượt trên tia đối AB,AC sao cho BD=CE=BC. Gọi giao điểm của MN với BE,CD lần lượt lag P,Q. Chứng minh P,Q lần lượt là trung điểm BE,CD
Theo dõi (0) 0 Trả lời -
Cho đường tròn (O;R) với dây BC cố định (BC không đi qua O). Gọi A là điểm chính giữa cung nhỏ BC. Điểm E thuộc cung lớn BC. Nối AE cắt dây BC tại D. Gọi I là trung điểm dây BC. Hạ CH vuông góc với AE. đường thẳng BE cắt CH tại M . Chứng minh AHCI nội tiếp
bởi Phạm Gia Hưng
28/05/2022
Cho đường tròn (O;R) với dây BC cố định (BC không đi qua O). Gọi A là điểm chính giữa cung nhỏ BC. Điểm E thuộc cung lớn BC. Nối AE cắt dây BC tại D. Gọi I là trung điểm dây BC. Hạ CH vuông góc với AE. đường thẳng BE cắt CH tại M
a) Chứng minh AHCI nội tiếp
b) Chứng minh AD.AE= AB^2
cần gấp câu 2
Theo dõi (0) 0 Trả lời -
Cho đường tròn tâm O đường kính AB=2R lấy điểm M thuộc đường tròn sao cho góc BAM=30độ. Trên tia đối của tia MA lấy điểm M sao cho MN=MB gọi I làm tâm đường tròn ngoại tiếp tam giác BAN. Chứng minh I thuộc đường tròn.
bởi Bùi Khôi
16/05/2022
Cho đường tròn tâm O đường kính AB=2R lấy điểm M thuộc đường tròn sao cho góc BAM=30độ. Trên tia đối của tia MA lấy điểm M sao cho MN=MB gọi I làm tâm đường tròn ngoại tiếp tam giác BAN chứng minh I thuộc đường tròn
Theo dõi (0) 0 Trả lời -
ADMICRO
Từ điểm A nằm ngoài đường tròn (O). Kẻ hai cát tuyến ABC( B nằm giữa A và C) và AEF( E nằm giữa A và F) sao cho CÂF = 45°, sđ cung BE= 30°. a/ Tính số đo cung CF. b/ Gọi I là giao điểm của BF và CE. Tính BIE.
bởi Phạm Khoa Khoa
04/04/2022
Từ điểm A nằm ngoài đường tròn (O). Kẻ hai cát tuyến ABC( B nằm giữa A và C) và AEF( E nằm giữa A và F) sao cho CÂF = 45°, sđ cung BE= 30°. a/ Tính số đo cung CF. b/ Gọi I là giao điểm của BF và CE. Tính BIE
Theo dõi (0) 0 Trả lời -
Một hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của hình đó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x
bởi Gia Hân
28/11/2021
1 hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của hình đó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC vuông tại A có góc B=30º, BC=16cm. Đường phân giác trong CD, đường phân giác ngoài Cx của
bởi Mei Huỳnh
22/11/2021
Cho tam giác ABC vuông tại A có <B=30º, BC=16cm. Đường phân giác trong CD, đường phân giác ngoài Cx của <C (D €AB)
a) Tính AB, AC, DC
b) Kẻ AM vg góc với Cx, AN vg góc với CD. C/m MN//BC
c) AN cắt BC tại E. tính diện tích của AECMTheo dõi (0) 0 Trả lời -
Cho hai đường tròn (O,R) và (O',R') tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn ( B thuộc (O), C thuộc (O') ). Chứng minh rằng tam giác ABC vuông.
bởi Doan Son
10/11/2021
Cho hai đường tròn (O,R) và (O',R') tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn ( B thuộc (O), C thuộc (O') )
a) CMR: tam giác ABC vuông
b) OO' cắt (O) tại D và cắt (O') tại E (D, E khác A). Đường thẳng DB cắt đường thẳng EC tại F. CMR: FA là tiếp tuyến chung của hai đường tròn.
c) CMR: BC=2căn(RR') và S bdec/S fde = (R^2+RR'+R'^2)/(R+R')^2
d) Vẽ AK vuông BC tại K. CMR: ba đường thẳng CO, O'B và AK đồng quy tại trung điểm của AK.Theo dõi (0) 0 Trả lời -
Cho hình chữ nhật 114 cm giảm chiều rộng 5 cm, tăng chiểu dài 8 cm. Diện tích không đổi tính diện tích lập phương trình.
bởi Nguyễn Nhật Thành
10/08/2021
cho hcn 114 cm giảm chiều rộng 5 cm tăng chiểu dài 8 cm diện tích ko đổi tính diện tích lập phương trình
Theo dõi (1) 0 Trả lời -
Cho ∆ABC có AB < AC < BC. Trên cạnh BC, AC lần lượt lấy các điểm M và N sao cho AN = AB = BM. Các đường thẳng AM và BN cắt nhau tại K. Gọi H là hình chiếu của K lên AB. Chứng minh rằng tâm đường tròn nội tiếp ∆ABC nằm trên KH
bởi Minhchau Trần
29/07/2021
Cho ∆ABC có AB < AC < BC. Trên cạnh BC, AC lần lượt lấy các điểm
M và N sao cho AN = AB = BM. Các đường thẳng AM và BN cắt nhau tại K. Gọi H là
hình chiếu của K lên AB. Chứng minh rằng :
a) Tâm đường tròn nội tiếp ∆ABC nằm trên KH
b) Các đường tròn nội tiếp các tam giác ACH và BCH tiếp xúc nhauMk đg cần gấp. TKS mn
Theo dõi (0) 0 Trả lời
